La funzione modulo o valore assoluto
La funzione valore assoluto (o funzione modulo) è una funzione in cui la variabile incognita è un argomento del valore assoluto. $$ f(x) = |x| $$
La funzione valore assoluto restituisce il valore della variabile indipendente con il segno positivo o nullo (non negativo).
Ad esempio, Il valore assoluto di -3 è 3
$$ | - 3 | = 3 $$
La funzione valore assoluto elimina il segno del valore (-3) e restituisce un valore positivo (3).
Per indicare il valore assoluto (modulo) uso due barre verticali vicino alla variabile x.
$$ f(x) = |x| $$
In alternativa, posso scrivere la funzione valore assoluto anche usando questa notazione
$$ y=|x| = \begin{cases} x \ \ \ se \ x \ge 0 \\ \\ -x \ \ \ se \ x \ < 0 \end{cases} $$
Vuol dire che la funzione assume
- l'espressione y=x se x è maggiore o uguale a zero.
- l'espressione y=-x se x è minore di zero
A volte è anche indicata come abs() ossia come abbreviazione di absolute value. In particolar modo in informatica.
$$ y = abs(x) $$
Posso ottenere la funzione valore assoluto anche usando la radice quadrata di una incognita elevata alla seconda. $$ y = |x| = \sqrt{x^2} $$
A cosa serve? La funzione valore assoluto è usata in diverse applicazioni. Ad esempio, è utile per calcolare la distanza tra due punti.
Un esempio pratico
Ecco qualche esempio pratico di valore assoluto.
Il valore assoluto di -3 è 3
$$ | - 3 | = 3 $$
Il valore assoluto di -4,2 è 4,2
$$ | -4,2 | = 4,2 $$
Il valore assoluti di 4 è 4
$$\ |4| = 4 \ $$
Il valore assoluto di -121 è 121
$$\ |-121| = 121 \ $$
Nota. Fa eccezione alla regola il valore zero (elemento nullo) che, non avendo segno, viene restituito tale e quale dalla funzione valore assoluto. $$ |0| = 0 $$
Il grafico della funzione valore assoluto
Il grafico del valore assoluto è sempre non negativo sull'asse delle ordinate (y), si trova sopra l'asse delle ascisse (x).
Un esempio classico della funzione valore assoluto è f(x)=|x| che sul diagramma cartesiano si rappresenta in questo modo
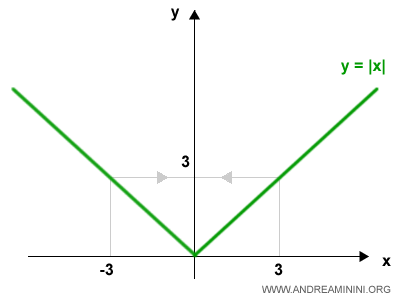
La funzione f(x)=|x| è composta da due semirette y=x per x>0 e y=-x per x<0 che convergono all'origine.
Nell'origine (0;0) si presenta una punto angoloso.
Pertanto, nell'origine la funzione è continua ma non derivabile.
Nota. L'argomento del valore assoluto può essere qualsiasi. Ad esempio f(x)=|2x| oppure f(x)=|x2+1| ecc. Quindi, non è detto che il grafico sia sempre composto da due semirette. Può presentarsi anche come una parabola o altra forma, a seconda dell’espressione nell’argomento. Ad esempio, se disegno il grafico del valore assoluto della funzione f(x)=|x3| ottengo una parabola.
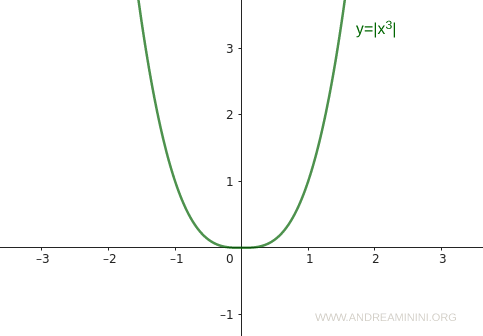
In ogni caso, comunque, i punti del grafico si trovano sopra l’asse delle x.
E così via.
