Funzione decrescente
Una funzione y=f(x) è detta funzione decrescente in un intervallo I=(a,b) se presi due punti qualsiasi x1, x2 dell'intervallo con x1<x2 risulta $$ f(x_1) \ge f(x_2) $$ oppure è detta funzione strettamente decrescente se risulta $$ f(x_1) > f(x_2) $$
Una funzione strettamente decrescente è anche detta decrescente in modo stretto.
Le funzioni decrescenti e strettamente decrescenti appartengono all'insieme delle funzioni monotòne.
Nota. Una funzione si dice monotòna in un intervallo quando è sempre crescente oppure decrescente nell'intervallo.
Esempio
Considero la funzione
$$ y=x^2 $$
Questa funzione è strettamente decrescente nell'intervallo (-4,0) perché presi due punti qualsiasi x1<x2 dell'intervallo è soddisfatta la relazione f(x1)>f(x2)
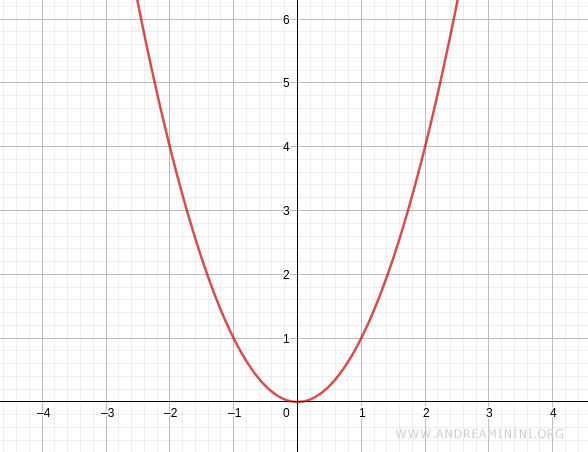
La stessa funzione non è decrescente nell'intervallo (0,4)
Nota. Lo studio della decrescenza di una funzione continua e derivabile posso ottenerlo anche studiando il segno della derivata prima f'(x) della funzione.
E così via.
