Funzione periodica

Cosa sono le funzioni periodiche

Una funzione $ y=f(x) $ è detta periodica di periodo $ T $, con $ T>0 $ se vale $$ f(x+kT)=f(x) $$ per ogni $ x $ del dominio e per ogni numero intero $ k $.

In una funzione periodica il grafico si ripete di periodo in periodo.

Di conseguenza, se una funzione è periodica di periodo T, allora è periodica anche per qualsiasi periodo multiplo di T.

$$ f(x+T) = f(x+kT) = f(x) $$

Questo accade perché i valori di $ x $, $ x+T $ e $ x+kT $ hanno la stessa immagine.

Ad esempio, se una funzione è periodica per un periodo T, allora lo è anche per 2T, 3T, 4T, ecc. Il periodo minore T è detto periodo principale.

Un esempio pratico

La funzione coseno è una funzione periodica di periodo T=2π.

$$ y = \cos(x) $$

Ad esempio, per x=0, x=2π la funzione f(x) assume lo stesso valore.

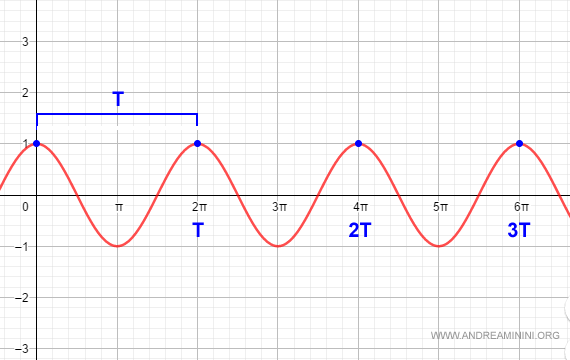
Anche per x=4π assume lo stesso valore. Lo stesso accade per x=6π e via dicendo.

$$ \cos(0) = \cos(2 \pi ) = \cos (4 \pi ) $$

In generale, la funzione $ f= \cos (x) $ ripete gli stessi valori del codominio per ogni multiplo del periodo T.

$$ \cos (x) = \cos(x+kT) $$

Quindi, è una funzione periodica con $ T= 2 \pi $.

Note

Alcune note a margine sulle funzioni periodiche:

• Una funzione periodica non è iniettiva
  In una funzione periodica esiste un periodo \( T \neq 0 \) tale che \( f(x+T)=f(x) \) per ogni \( x \) del dominio. Di conseguenza, lo stesso valore del codominio viene assunto da infiniti valori distinti del dominio, separati da multipli di \( T \). Per questo motivo, se una funzione è periodica, non può essere iniettiva. Viceversa, se una funzione è iniettiva, allora non è periodica.

E così via.