Tipi di funzioni

Esistono diverse tipologie di funzioni. Ecco le principali

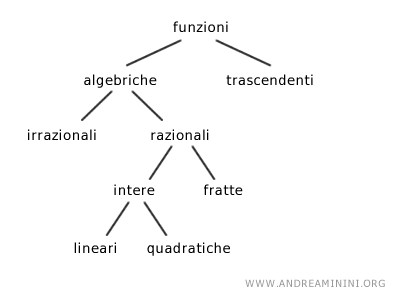
• Funzione algebrica
  Una funzione è detta algebrica se l'espressione f(x) contiene solo operazioni di addizione, sottrazione, moltiplicazione, elevamento a potenza, radici.

  Esempio. Sono funzioni funzioni algebriche. $$y=2x^2+x$$ $$y= \frac{x+1}{x-1}$$ $$y = x - \sqrt{x}$$

• Funzione trascendente
  Una funzione è detta trascendente quando non è algebrica.

  Esempio. Sono funzioni trascendenti quelle in cui compare nell'espressione l'esponenziale a^x, il logaritmo o una funzione trigonometrica. $$y=2^x$$ $$y= \sin(x)$$ $$y = \log(x)$$

A loro volta le funzioni algebriche si dividono in razionali e irrazionali

• Funzioni razionali
  Una funzione è detta razionale se la variabile indipendente x non è l'argomento di una radice

  Esempio. Sono funzioni razionali $$y = x^2+1$$ $$y = \frac{2x+1}{x-1}$$ $$y = x^3-x^2+2$$

• Funzione irrazionale
  La funzione è detta irrazionale se la variabile indipendente x è l'argomento di almeno una radice.

  Esempio. Sono funzioni irrazionali $$y = \sqrt{x}$$ $$y = x - \sqrt{x}$$ $$y = \frac{ \sqrt{x} }{x+1}$$

A loro volta le funzioni razionali si dividono in intere o fratte

• Funzione intera o polinomiale
  Una funzione è detta intera se l'espressione f(x) è un polinomio di qualsiasi grado
  • Funzione lineare
    se il polinomio è di grado 1
  • Funzione quadratica
    se il polinomio è di grado 2

  Esempio. Sono funzioni intere lineari $$y = 2x+1$$ $$y = 5-3x$$ Sono funzioni intere quadratiche $$y = x^2-3x+1$$ $$y = 3x^2+2x+1$$ Altre funzioni intere né lineari né quadratiche $$y = 2x^3+x^2-1$$ $$y = x^5-3x^3+2$$

• Funzione razionale fratta
  La funzione è detta razionale fratta quando l'espressione f(x) è il quoziente di due polinomi.

  Esempio. Sono funzioni razionali fratte $$y = \frac{x+1}{x-1}$$ $$y = \frac{x^2+2x-1}{x^3+x^2+4}$$ $$y = \frac{x^4+x-1}{x^2+3}$$

E così via