Le funzioni suriettive
Cos'è una funzione suriettiva
Una funzione matematica è detta funzione suriettiva (o surgettiva) se ogni elemento del codominio è un'immagine di almeno un elemento del dominio. $$ \forall \: y \: \exists \: x \: \:\: f(x)=y $$
Con i diagrammi di Venn il concetto di suriettività dovrebbe essere più chiaro.
Ogni elemento del codominio (B) della funzione è raggiungibile da almeno un elemento del dominio (A) della funzione suriettiva.
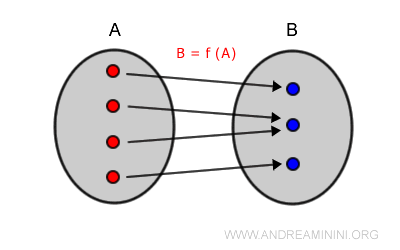
In simboli una funzione f è suriettiva se
$$ \forall \ y \in B \ \ \exists \ \ x \in \ A \ \ | \ \ f(x)=y $$
Nota. Non occorre che ci sia un solo elemento x ∈ A per ogni y ∈ B. Un elemento del codominio (B) potrebbe essere anche raggiunto da più di un elemento del dominio. L'importante è che ogni elemento y del codominio sia raggiungibile da qualche elemento dell'insieme del dominio tramite la funzione f(x).
Quindi, ogni elemento di B (codominio) ha almeno una controimmagine nell'insieme A (dominio).
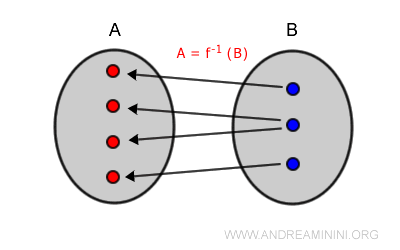
Se una funzione è suriettiva l'insieme di arrivo B è uguale al codominio della funzione.
Pertanto, la suriettività della funzione dipende da quale insieme di arrivo scelgo per la funzione.
Nota. Posso sempre rendere una funzione suriettiva se non lo è. Per farlo mi basta restringere l'insieme di arrivo B all'insieme delle immagini della f(x), ossia al codominio della funzione. Ad esempio, la funzione y=f(x)=2x non è suriettiva se l'insieme di arrivo è B, perché l'elemento 10 non è il doppio di nessun elemento dell'insieme A.
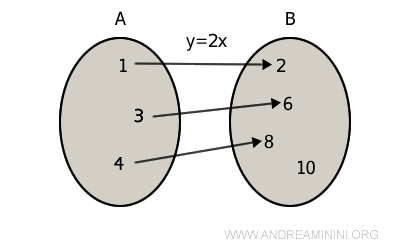
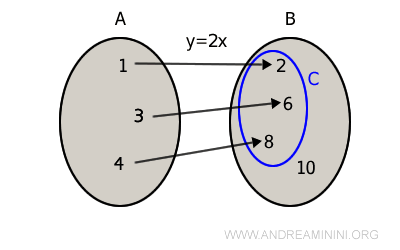
Tuttavia, se restringo l'insieme di arrivo all'insieme delle immagini C={ 2, 6, 8 }, ossia al codominio, la funzione y=f(x)=2x diventa suriettiva.
Esempio
Ad esempio, questa funzione è suriettiva nell'intervallo y∈[a,b] perché per ogni valore y esiste almeno una controimmagine x.
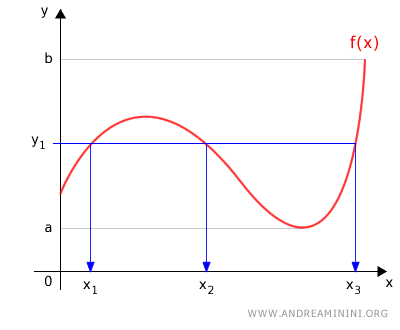
La stessa funzione non è suriettiva nell'intervallo y∈[0,b] perché nel tratto [0,a] gli elementi di y non hanno alcuna controimmagine x.
Pertanto, per rendere suriettiva la funzione f(x) è sufficiente considerare l'intervallo [a,b] delle immagini come insieme di arrivo anziché l'intervallo [0,b].
Restringendo l'insieme di arrivo all'insieme delle immagini [a,b] la funzione f(x) diventa suriettiva.
Un esempio pratico
Esempio 1
Se considero il dominio e il codominio della funzione coincidenti con l'insieme reale R
$$ f: R \rightarrow R $$
la seguente funzione reale è suriettiva
$$ f(x) = x+1 $$
perché ogni elemento del codominio y∈R è ottenibile tramite la funzione con almeno un elemento x∈R.
| x | y=f(x) |
|---|---|
| x=-3 | -2 |
| x=-2 | -1 |
| x=-1 | 0 |
| x=0 | 1 |
| x=1 | 2 |
| x=2 | 3 |
| x=3 | 4 |
Tutti gli elementi y sono collegati con almeno un elemento x
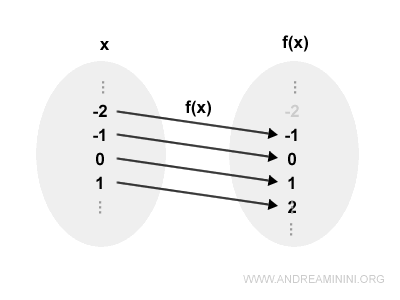
Quindi, la funzione f(x)=x+1 è suriettiva nell'insieme dei numeri reali.
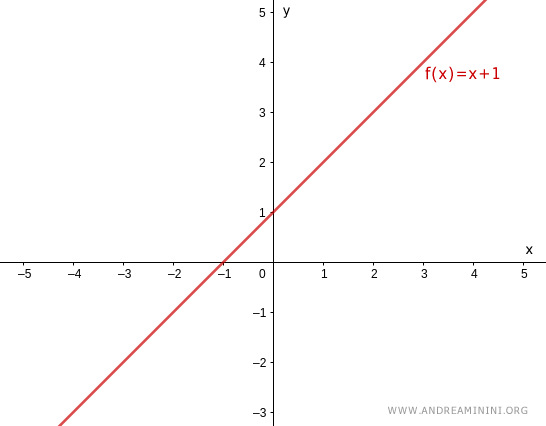
Esempio 2
Se considero il dominio e il codominio della funzione coincidenti con l'insieme reale R
$$ f: R \rightarrow R $$
questa funzione reale non è suriettiva
$$ f(x) = x^2 $$
perché alcuni elementi del codominio y∈R non sono raggiungibili da nessun elemento x∈R.
| x | y=f(x) |
|---|---|
| x=-3 | 9 |
| x=-2 | 4 |
| x=-1 | 1 |
| x=0 | 0 |
| x=1 | 1 |
| x=2 | 4 |
| x=3 | 9 |
Ad esempio, gli elementi negativi y<0 non sono raggiungibili da nessun x con la funzione f(x)=x2.
Nessun numero x elevato al quadrato dà come risultato -2 o -3.
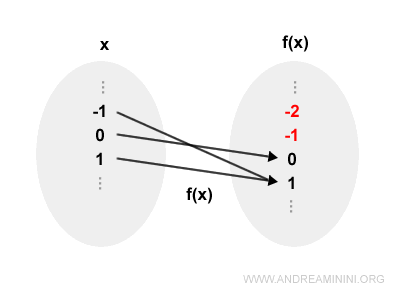
Quindi, la funzione f(x)=x2 non è suriettiva se considero come insieme di arrivo l'insieme dei numeri reali.
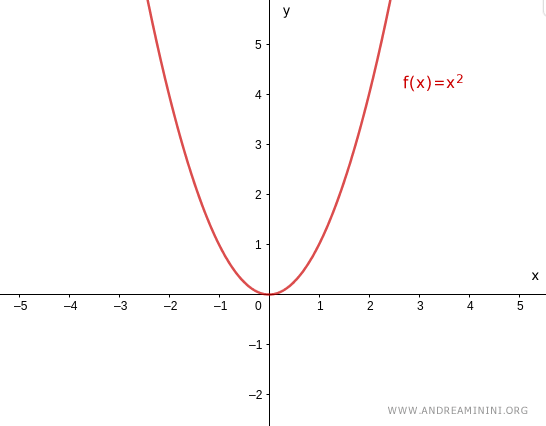
Nota. Per far diventare suriettiva anche la funzione x2 devo considerare un insieme di arrivo più ridotto. Ad esempio, prendendo come insieme di arrivo l'insieme dei numeri reali non negativi R+∪{0} anche la funzione x2 diventa suriettiva. $$ f: R \rightarrow R^+ \cup \{ 0 \} $$ perché ora ogni elemento y=f(x)≥0 dell'insieme di arrivo è raggiungibile da almeno un elemento x dell'insieme di partenza (dominio).
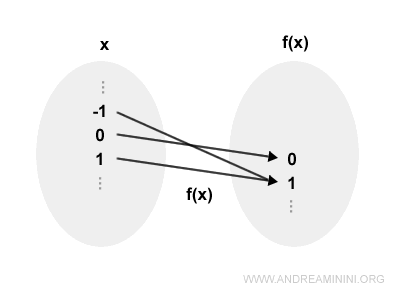
E così via.
