La funzione continua
Una funzione f(x) è detta funzione continua in un punto x0 se il limite della funzione per x che tende a x0 è uguale a f(x0). $$ \lim_{x \rightarrow x_0} f(x) = f(x_0) $$
Il grafico una funzione continua si presenta con un tratto continuo e senza alcuna interruzione.
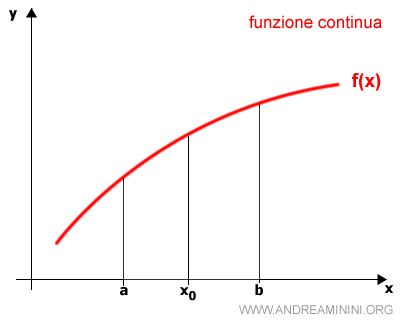
Le funzioni continue in un intervallo
Una funzione è continua in un intervallo [a,b] se è continua in tutti i punti dell'intervallo.
$$ \lim_{x \rightarrow x_0} f(x) = f(x_0) \:\:\: \forall x_0 \in [a,b] $$
Nel caso particolare degli estremi dell'intervallo si calcola soltanto il limite destro per l'estremo iniziale a
$$ \lim_{x \rightarrow a^+} f(x) = f(a) $$
e il limite sinistro per l'estremo terminale b
$$ \lim_{x \rightarrow b^-} f(x) = f(b) $$
Un esempio pratico
Ho la funzione
$$ f(x) = x^2 $$
Verifico se la funzione è continua in x0=2.
$$ \lim_{x \rightarrow 2} x^2 = 4 $$
Nel punto x0=2 la funzione ha valore quattro
$$ f(2) = 4 $$
Il limite e la funzione coincidono
$$ \lim_{x \rightarrow 2} x^2 = f(2) $$
Pertanto, la funzione x2 è continua nel punto x0=2.
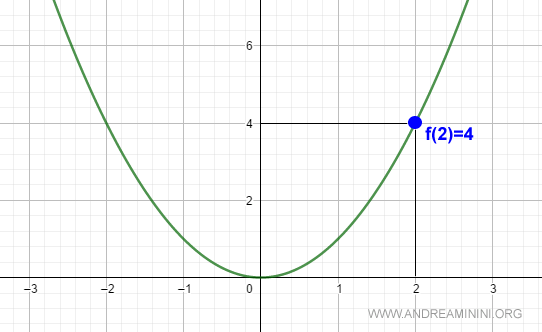
Lo stesso si può dire per qualsiasi altro punto x del campo di esistenza (-∞,∞) della funzione.
E così via.
