Funzione limitata e illimitata
Cos'è una funzione limitata?
Una funzione limitata è una funzione che assume valori f(x) limitati tra un minimo e massimo.
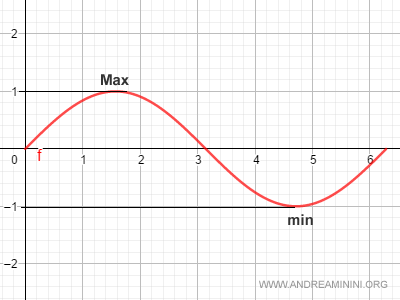
Dal punto di vista geometrico il grafico di una funzione limitata è racchiuso tra due rette parallele all'asse delle ascisse.
In una funzione limitata l'insieme delle immagini è limitato tra due numeri reali:
- Il minimo. Il valore più basso della funzione f(x) in un intervallo [a,b]
- Il massimo. Il valore più alto della funzione f(x) in un intervallo [a,b]
Se non è possibile trovare due numeri reali che limitino l'insieme delle immagini, la funzione è detta funzione illimitata.
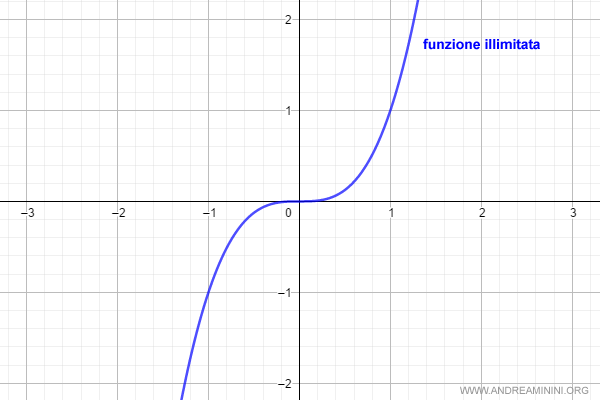
Esempio di funzione illimitata. La funzione x3 è una funzione illimitata. Non ha un minimo, né un massimo.
Una funzione limitata è limitata sia inferiormente che superiormente.
Un esempio pratico
Prendo in considerazione la funzione seno
$$ f(x) = \sin(x) $$
Il dominio della funzione è l'insieme dei numeri reali
$$ Dom(f)=R $$
L'immagine della funzione è un insieme infinito di valori compresi nell'intervallo chiuso [-1,1]
$$ Im(f) = [-1,1] $$
L'insieme delle immagini è limitato sia inferiormente che superiormente.
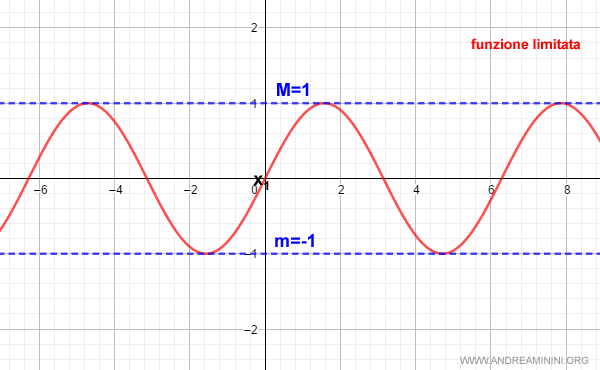
La funzione f(x) ha sia un valore massimo che un valore minimo
$$ M=1 $$
$$ m=-1 $$
Pertanto, la funzione seno è una funzione limitata nel suo dominio.
Funzione limitata superiormente
Una funzione f(x) definita nell'intervallo (a,b) è limitata superiormente se almeno una di queste condizioni è soddisfatta:
- esiste un numero reale M tale che f(x)≤M per ogni x ∈ (a,b).
- l'immagine della funzione f(x) è un insieme limitato superiormente
- l'immagine della funzione f(x) ha un estremo superiore finito $$ sup(Im(f))<+∞ $$
Se nessuna delle condizioni è soddisfatta, la funzione è illimitata superiormente.
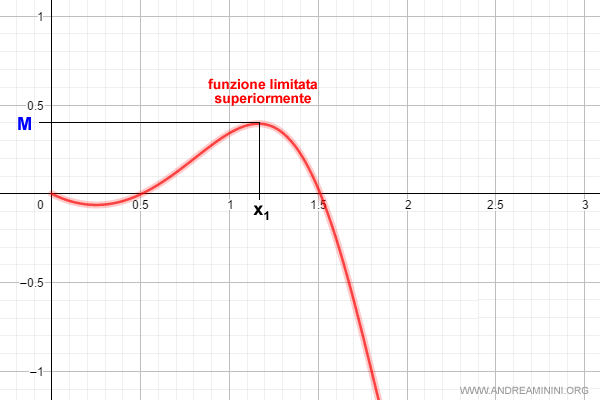
Esempio. Un esempio di funzione limitata superiormente. La f(x) ha un valore massimo (M).
Funzione illimitata superiormente
Una funzione f(x) definita in (a,b) è illimitata superiormente nel suo dominio se almeno una delle seguenti condizioni è soddisfatta
- per ogni M>0 esiste un x ∈ (a,b) tale che f(x)>M
- l'immagine di f(x) è un insieme illimitato superiormente
- l'immagine di f(x) ha un estremo superiore infinito $$ sup(Im(f))=+∞ $$
Esempio. Un esempio di funzione illimitata superiormente.
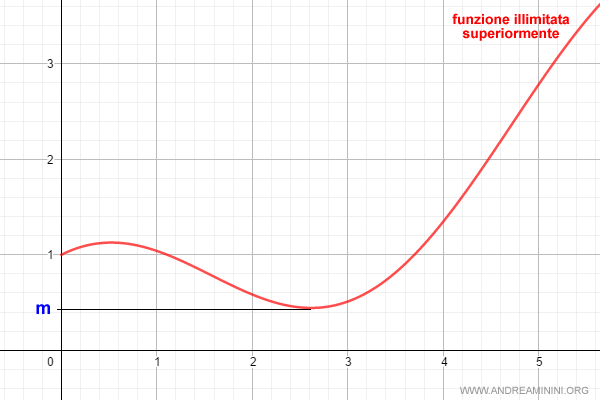
Funzione limitata inferiormente
Una funzione f(x) definita nell'intervallo (a,b) è limitata inferiormente se almeno una di queste condizioni è soddisfatta:
- esiste un numero reale m tale che f(x)≥m per ogni x ∈ (a,b).
- l'immagine della funzione f(x) è un insieme limitato inferiormente
- l'immagine della funzione f(x) ha un estremo inferiore finito $$ inf(Im(f))>-∞ $$
Se nessuna delle condizioni è soddisfatta, la funzione è illimitata inferiormente.
Esempio. Un esempio di funzione limitata inferiormente. La funzione ha un valore minimo (m).
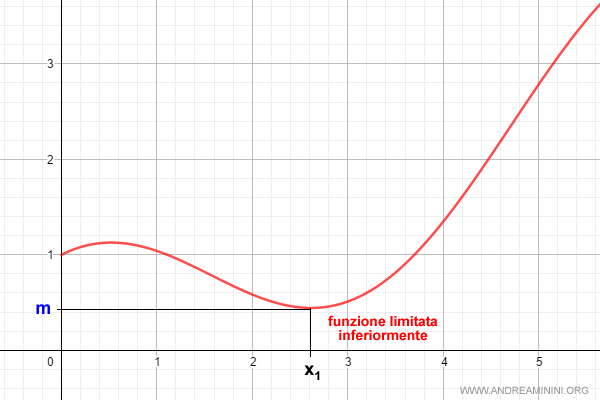
Funzione illimitata inferiormente
Una funzione f(x) definita in (a,b) è illimitata inferiormente nel suo dominio se almeno una delle seguenti condizioni è soddisfatta
- per ogni m di R esiste un x ∈ (a,b) tale che f(x)<m
- l'immagine di f(x) è un insieme illimitato inferiormente
- l'immagine di f(x) ha un estremo inferiore infinito $$ inf(Im(f))=-∞ $$
Esempio. Un esempio di funzione illimitata inferiormente.
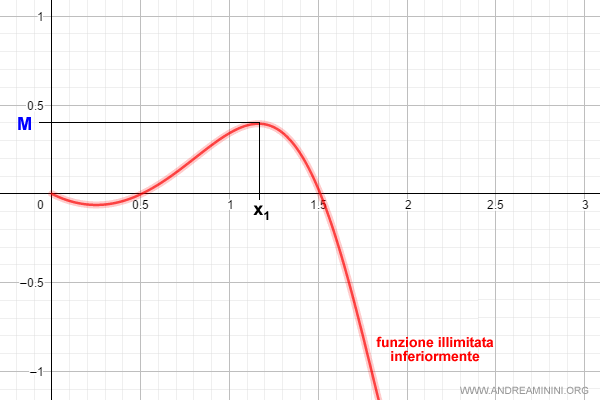
E così via.
