Controimmagini di una funzione
La controimmagine (o preimmagine) di un elemento del codominio \( y \in Y \) di una funzione \( f: X \to Y \) è l'insieme di tutti gli elementi del dominio \( x \in X \) che vengono mappati in quell'elemento specifico del codominio \( f(x) = y \). La controimmagine di \( y \) si indica con il simbolo \( f^{-1}(\{y\}) \). $$ f^{-1}(\{y\}) = \{ x \in X \mid f(x) = y \} $$
In altre parole, la controimmagine di un elemento $ y $ del codominio $ Y $ è l'insieme di tutti i valori nel dominio $ X $ che, una volta "passati" attraverso la funzione $ f(x) $, danno come risultato quell'elemento del codominio $ y = f(x) $.
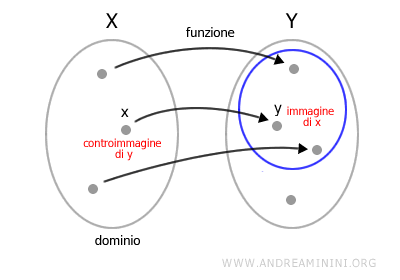
In generale, la controimmagine di un insieme Y attraverso una funzione y=f(x) è l'insieme degli elementi del dominio X della funzione che vengono mappati in quell'insieme dal codominio.
La controimmagine di un insieme descrive "da dove vengono" gli elementi mappati in quell'insieme attraverso la funzione \( f \).
La controimmagine \( f^{-1}(y) \) di un elemento \( y \) del codominio non è necessariamente una funzione inversa, perché può essere una relazione che associa un singolo elemento del codominio a più elementi del dominio.
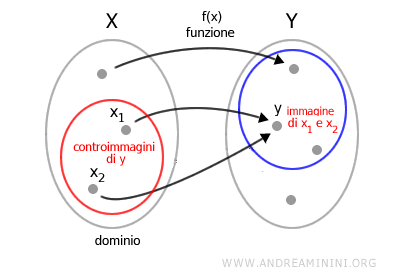
Questo accade perché, in generale, una funzione non deve essere iniettiva. Cioè, un singolo elemento del codominio può corrispondere a più di un elemento del dominio.
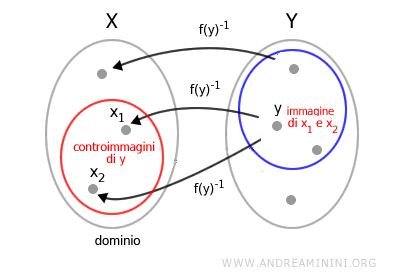
La controimmagine è sempre definita, anche se la funzione non è iniettiva o suriettiva.
Inoltre, la controimmagine di un insieme può essere anche un insieme vuoto se nessun elemento del dominio viene mappato.
Differenza tra funzione e relazione. Una funzione associa ogni elemento del dominio a uno e un solo elemento del codominio. Una relazione, invece, può associare un elemento del codominio a uno o più elementi del dominio. Quindi, tutte le funzioni sono relazioni ma solo alcune relazioni sono funzioni.
Un esempio pratico
Considero la funzione \( f(x) = x^2 \).
Il dominio è l'insieme dei numeri reali \( \mathbb{R} \), e il codominio è l'insieme dei numeri reali non negativi \( \mathbb{R}^{\geq 0} \).
Se prendo un numero nel codominio, ad esempio \( 4 \), la controimmagine di \( 4 \) è l'insieme di tutti i numeri \( x \) nel dominio che, quando elevati al quadrato, danno \( 4 \).
$$ f^{-1}(\{4\}) = \{ -2, 2 \} $$
In questo caso: sono $ -2 $ e $ 2 $ perché sia \( (-2)^2 = 4 \) sia \( 2^2 = 4 \).
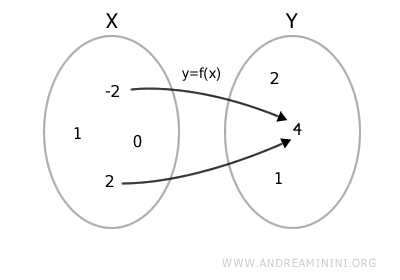
Quindi, la controimmagine di \( 4 \) è l'insieme dei numeri \( -2 \) e \( 2 \), perché sono questi i numeri che, passati attraverso la funzione \( x^2 \), danno come risultato \( 4 \).
Nota. In questo esempio le controimmagini del codominio $ Y $ non sono una funzione inversa ma solo una relazione inversa.
Le proprietà delle controimmagini
Alcune proprietà utili delle controimmagini di una funzione:
- Controimmagine dell'unione
La controimmagine dell'unione di due insiemi è l'unione delle controimmagini: $$ f^{-1}(A \cup B) = f^{-1}(A) \cup f^{-1}(B) $$ - Controimmagine dell'intersezione
La controimmagine dell'intersezione di due insiemi è l'intersezione delle controimmagini: $$ f^{-1}(A \cap B) = f^{-1}(A) \cap f^{-1}(B) $$ - Controimmagine del complementare
La controimmagine del complementare di un insieme è il complementare della controimmagine: $$ f^{-1}(Y \setminus A) = X \setminus f^{-1}(A) $$
Queste proprietà sono anche conosciute come proprietà della "preservazione della controimmagine rispetto all'unione, l'intersezione e la differenza".
Esempio
Considero ora la funzione
$$ f(x) = \sqrt{x} $$
Dove \( f: \mathbb{R}^{\geq 0} \to \mathbb{R}^{\geq 0} \) sapendo che la funzione radice quadrata è definita solo per \( x \geq 0 \).
Prendo due insiemi del dominio.
$$ A_1 = [0, 1) $$
$$ A_2 = [4, 9] $$
La controimmagine dell'intervallo \( A_1 = [0, 1) \) è
$$ f^{-1}(A_1) = \{ x \in \mathbb{R}^{\geq 0} \mid \sqrt{x} \in [0, 1) \} = [0, 1) $$
La controimmagine dell'intervallo \( A_2 = [4, 9] \) è
$$ f^{-1}(A_2) = \{ x \in \mathbb{R}^{\geq 0} \mid \sqrt{x} \in [4, 9] \} = [16, 81] $$
A questo punto verifico le tre operazioni sugli insiemi:
A] Unione
L'unione delle controimmagini è la seguente:
$$ f^{-1}(A_1) \cup f^{-1}(A_2) = [0, 1) \cup [16, 81] $$
L'unione degli intervalli è:
$$ A_1 \cup A_2 = [0, 1) \cup [4, 9] $$
La controimmagine dell'unione è
$$ f^{-1}(A_1 \cup A_2) = f^{-1}([0, 1) \cup [4, 9]) = [0, 1) \cup [16, 81] $$
Questo conferma la preservazione dell'unione per la funzione \( f(x) = \sqrt{x} \).
$$ f^{-1}(A_1 \cup A_2) = f^{-1}(A_1) \cup f^{-1}(A_2) $$
B] Intersezione
L'intersezione delle controimmagini è l'insieme vuoto perché non c'è sovrapposizione tra \( [0, 1) \) e \( [4, 9] \).
$$ f^{-1}(A_1) \cap f^{-1}(A_2) = [0, 1) \cap [16, 81] ] = \emptyset $$
Anche la controimmagine dell'intersezione è l'insieme vuoto.
$$ f^{-1}(A_1 \cap A_2) = f^{-1}(\emptyset) = \emptyset $$
Questo conferma la preservazione dell'intersezione per la funzione \( f(x) = \sqrt{x} \).
$$ f^{-1}(A_1 \cap A_2) = f^{-1}(A_1) \cap f^{-1}(A_2) $$
C] Complementare
Considero ora il complementare dell'insieme \( A_1 = [0, 1) \) nel dominio \( \mathbb{R}^{+} \), che è:
$$ \mathbb{R}^{+} \setminus A_1 = [1, \infty) $$
La controimmagine del complementare è:
$$ f^{-1}(\mathbb{R}^{+} \setminus A_1) = f^{-1}([1, \infty)) = [1, \infty) $$
Il complementare della controimmagine di \( A_1 \) è:
$$ \mathbb{R}^{+} \setminus f^{-1}(A_1) = \mathbb{R}^{+} \setminus [0, 1) = [1, \infty) $$
Questo conferma la preservazione del complementare per la funzione \( f(x) = \sqrt{x} \).
$$ f^{-1}(\mathbb{R}^{+} \setminus A_1) = \mathbb{R}^{+} \setminus f^{-1}(A_1) $$
In questo esempio tutte le proprietà delle controimmagini rispetto alle operazioni insiemistiche (unione, intersezione, complementare) sono state soddisfatte.
E così via.
