Funzione omografica
Una funzione omografica è una funzione razionale del tipo $$ f(x) = \frac{ax + b}{cx + d} $$ dove \(a\), \(b\), \(c\) e \(d\) sono coefficienti reali, e \(c \neq 0\) e \(ad - bc \neq 0\) per evitare casi degeneri.
Il dominio della funzione omografica è dato da tutti i valori reali di \(x\) tranne il punto in cui il denominatore si annulla, cioè \(x \neq -\frac{d}{c}\).
A seconda dei valori di \(a\), \(b\), \(c\) e \(d\), la funzione omografica può mostrare comportamenti molto diversi, inclusa la possibilità di essere monotona crescente o decrescente, avere un punto di flesso o un'iperbole.
Perché si chiama omografica? Il termine "omografica" deriva dall'unione di due radici greche: "homo" (ὁμός), che significa "uguale", e "graph" (γραφή), che significa "scrittura" o "disegno". Il nome si riferisce al fatto che una funzione omografica rappresenta una trasformazione che mantiene invariati alcuni aspetti geometrici delle figure, come rette e cerchi, quando si applica al piano complesso. In altre parole, una trasformazione omografica (o funzione omografica) trasforma rette in altre rette e cerchi in altri cerchi, mantenendo una "somiglianza" tra le figure originali e quelle trasformate. Questa proprietà di mantenere la "forma" delle figure, pur trasformandole, è alla base del nome "omografica". Grazie a queste proprietà le funzioni omografiche hanno diverse applicazioni pratiche nei modelli economici, fisici e geometrici.
Una funzione omografica presenta due asintoti: verticale e orizzontale
- Asintoto verticale: Si trova in corrispondenza del valore di \(x\) che annulla il denominatore, ossia \(x = -\frac{d}{c}\).
- Asintoto orizzontale: Se \(c \neq 0\), l'asintoto orizzontale è dato dal rapporto tra i coefficienti \(a\) e \(c\), ovvero \(y = \frac{a}{c}\).
Per trovare le eventuali intersezioni con l'asse delle ascisse, parto dall'ipotesi \(f(x) = 0\) e risolvo l'equazione \(ax + b = 0\), quindi \(x = -\frac{b}{a}\) ammesso che \(a \neq 0\). Per quelle con l'asse delle ordinate, invece, assegno \(x = 0\) e ricavo \(y = \frac{b}{d}\) purché \(d \neq 0\)).
Un esempio pratico
Considero la funzione omografica
$$ y = \frac{3x-2}{x-1} $$
In questo caso i coefficienti sono $ a=3 $ , $ b=-2 $, $ c=1 $, $ d=-1 $
Le condizioni sono soddisfatte:
- $ c = 1 \ne 0 $
- $ ad-bc \ne 0 $
$ 3 \cdot (-1) - (-2) \cdot 1 \ne 0 $
$-3 + 2 \ne 0 $
$ -1 \ne 0 $
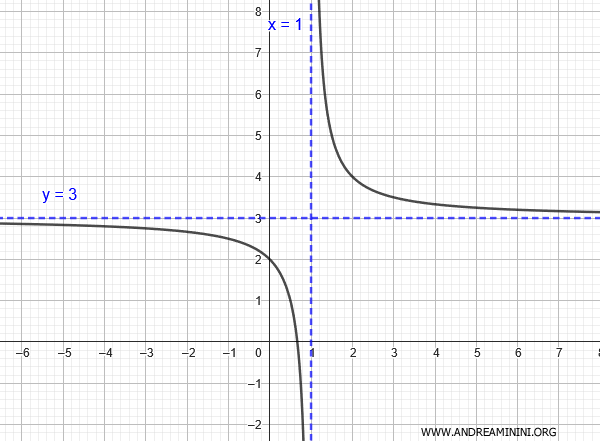
Gli asintoti della funzione omografica sono
$$ x = -\frac{d}{c} = - \frac{-1}{1} = 1 $$
$$ y = \frac{a}{c} = \frac{3}{1} = 3 $$
Dagli asintoti posso dedurre che la funzione omografica è un'iperbole equilatera con gli asintoti paralleli agli assi cartesiani centrata nel punto $ C(1;3) $
L'equazione dell'iperbole equilatera posso trovarla anche trasformando la funzione omografica nella forma $ (x-x_0) \cdot (y-y_0) = \pm 1 $
$$ y = \frac{3x-2}{x-1} $$
$$ y (x-1) =3x-2 $$
$$ xy - y =3x-2 $$
Porto tutti i termini con la x a sinistra e gli altri a destra
$$ xy - 3x = y-2 $$
$$ x(y-3) = y-2 $$
Divido per (y-3) entrambi i lati dell'equazione
$$ \frac{ x(y-3) }{y-3} = \frac {y-2}{y-3} $$
$$ x = \frac{y-2}{y-3} $$
Aggiungo e sottraggo 1 al numeratore
$$ x = \frac{y-2+1-1}{y-3} $$
$$ x = \frac{y-3+1}{y-3} $$
$$ x = \frac{y-3}{y-3} + \frac{1}{y-3} $$
$$ x = 1 + \frac{1}{y-3} $$
$$ x -1= \frac{1}{y-3} $$
$$ ( x -1 ) \cdot (y-3) = 1 $$
Quest'ultima è l'equazione dell'iperbole equilatera con gli asintoti paralleli agli assi cartesiani e il centro nel punto $ (1;3) $
Per trovare l'eventuale intersezione con l'asse x risolvo l'equazione $ y = 0 $
$$ \frac{3x-2}{x-1} = 0 $$
$$ \frac{3x-2}{x-1} \cdot (x-1) = 0 \cdot (x-1) $$
$$ 3x-2 = 0 $$
$$ 3x = 2 $$
$$ x = \frac{2}{3} $$
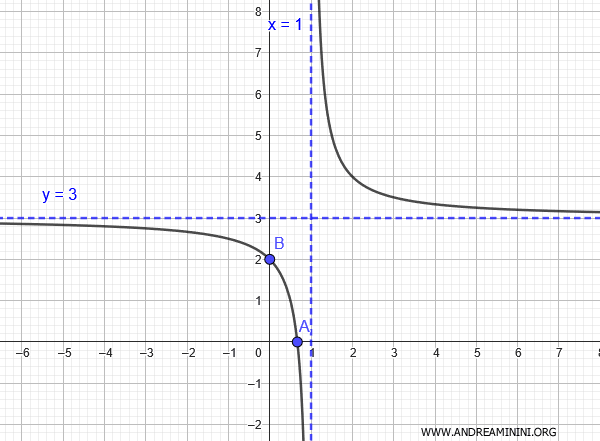
Quindi, la funzione passa nel punto $ A (x;y)= ( \frac{2}{3};0) $
Per trovare l'eventuale intersezione con l'asse y assegno $ x = 0 $ e ricavo la $ y $
$$ y = \frac{3x-2}{x-1} $$
$$ y = \frac{3 \cdot 0-2}{0-1} $$
$$ y = \frac{-2}{-1} $$
$$ y = 2 $$
Quindi, la funzione interseca l'asse x nel punto $ B (x;y)= (0;2) $
I casi degeneri
Quando la funzione omografica $ y = \frac{ax + b}{cx + d} $ ha il coefficiente $ c = 0 $ nullo oppure $ ad-bc= 0 $ degenera in una retta.
1] Se c = 0
Vediamo cosa accade alla funzione omografica se c=0
$$ y = \frac{ax + b}{cx + d} $$
$$ y = \frac{ax + b}{0 \cdot x + d} $$
$$ y = \frac{ax + b}{d} $$
$$ y = \frac{a}{d} x + \frac{a}{d} $$
Quest'ultima è l'equazione di una retta.
2] Se ad-bc = 0
Vediamo cosa succede se ad-bc=0.
$$ ad - bc = 0 $$
$$ ad = bc $$
$$ \frac{a}{c} =\frac{b}{d} $$
Assegno $ m = \frac{a}{c} =\frac{b}{d} $
Quindi ricavo le variabili $ a $ e $ b $
$$ \begin{cases} a = \frac{b}{d} \cdot c \\ \\ b = \frac{a}{c} \cdot d \end{cases} $$
$$ \begin{cases} a = m \cdot c \\ \\ b = m \cdot d \end{cases} $$
Sostituisco $ a=mc $ e $ b=md $ nella funzione omografica
$$ y = \frac{ax + b}{cx + d} $$
$$ y = \frac{mcx + md}{cx + d} $$
$$ y = \frac{m \cdot (cx + d)}{cx + d} $$
$$ y = m $$
Quest'ultima è una retta parallela all'asse x.
E così via.
