Punti di accumulazione
Dato un insieme I di numeri reali, un punto x0 è un punto di accumulazione per l'insieme I se preso un qualunque δ>0 esiste almeno un punto reale x di I tale che $$ 0 \ne |x-x_0| < δ $$
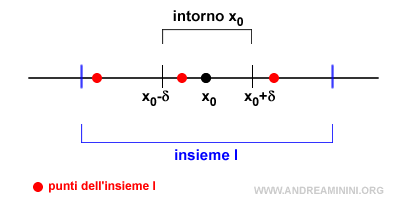
Se nell'intorno (x0-δ,x0+δ) c'è almeno un punto x dell'insieme I, distinto da x0, allora x0 è un punto di accumulazione per l'insieme I.
Nota. Se l'insieme I è composto da un solo punto [a,b] con a=b allora non esiste un punto di accumulazione per l'insieme i perché nell'intorno di x0 non ci sono altri punti diversi da x0=a.
Il caso degli intervalli chiusi e aperti
Devo distinguere tra intervalli chiusi e aperti
- Nell'intervallo chiuso [a,b] con a<b sono punti di accumulazione per [a,b] tutti i punti dell'intervallo.
- Nell'intervallo aperto (a,b) con a<b sono punti di accumulazione per (a,b) tutti i punti dell'intervallo e anche gli estremi a e b.
Quindi, i punti di accumulazione di un insieme aperto (a,b) sono gli stessi dell'intervallo chiuso [a,b].
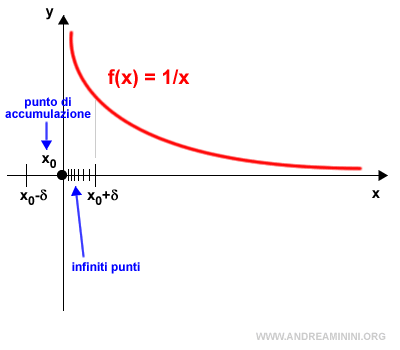
Esistono infiniti punti reali nell'intorno
Se l'insieme I è un sottoinsieme dell'insieme R di numeri reali $$ I⊆R $$ allora il punto x0∈R è un punto di accumulazione per I soltanto se nell'intorno (x0-δ,x0+δ) esistono infiniti punti di I diversi da x0.
Dimostrazione
Ipotizzo che x0 sia un punto di accumulazione e per assurdo che ci sia un numero finito di k punti di R nell'intorno di x0 per δ>0.
$$ | x_0 - x_i | < δ \:\:\: \forall i=1,...,k $$
Ora fisso un nuovo δ1 pari alla differenza minima |x0_xi|
$$ δ_1 = min| x_0 - x_i | \:\:\: \forall i=1,...,k $$
Nel nuovo intorno (x0-δ1,x0+δ1) non ci sarebbero punti di accumulazione diversi da x0.
$$ (x_0 - δ_1, x_0+δ_1) $$
Questo però è impossibile perché x0 è un punto di accumulazione per l'ipotesi iniziale.
Pertanto, se x0 è un punto di accumulazione nell'insieme dei numeri reali R, nell'intorno (x0-δ,x0+δ) devono esistere infiniti punti di R.
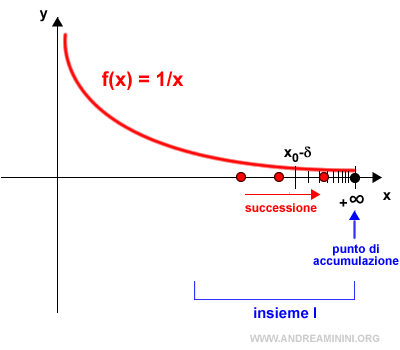
Le successioni estratte dall'intorno convergono al punto di accumulazione
Se x0 è un punto di accumulazione per l'insieme I di R, allora esiste una successione estratta di xn punti di I, diversi da x0, che converge a x0.
Dimostrazione
Dato un qualsiasi numero naturale n di N per definire l'intorno δ
$$ δ = \frac{1}{n} $$
Definisco un intorno del punto x0
$$ ( x_0 - δ, x_0 +δ ) $$
Essendo x0 un punto di accumulazione, nell'intorno (x0-δ,x0+δ) ci sono infiniti punti reali dell'insieme I diversi da x0.
$$ x_0 - \frac{1}{n} < x_n \ < x_0 + \frac{1}{n} $$
La precedente diseguaglianza definisce tre successioni estratte dell'insieme I per ogni n∈N
Calcolo il limite delle tre successioni per n tendente a infinito.
$$ \lim_{n→∞} x_0 - \frac{1}{n} < \lim_{n→∞} x_n \ < \lim_{n→∞} x_0 + \frac{1}{n} $$
I limiti della prima e della terza successioni convergono a x0 per n→∞
$$ x_0 < \lim_{n→∞} x_n \ < x_0 $$
Pertanto, per il teorema del confronto dei limiti anche il limite della successione estratta intermedia è convergente a x0.
E questo dimostra il teorema.
Dato un punto di accumulazione x0 per l'insieme I, se qualsiasi successione estratta xn di punti dell'insieme I-{x0} convergente a x0 genera una successione f(xn) convergente a l, allora la funzione f(x) ha un limite uguale a l per x che tende a x0. $$ \lim_{x \rightarrow x_0} f(x) = l $$
Esempio
Data la funzione f(x)=x2+1 il punto x0=0 è un punto di accumulazione rispetto all'insiemte I=(-1,0).
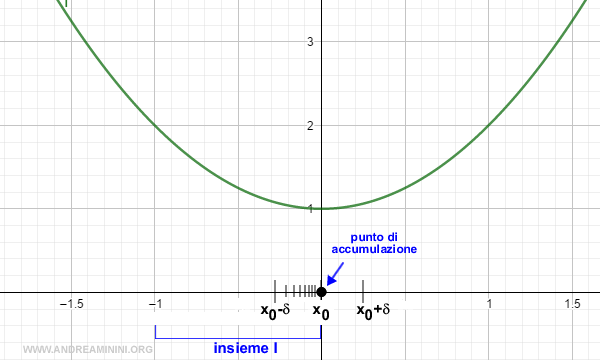
Preso un intorno (x0-δ,x0+δ) ogni successione estratta xn dall'insieme I che converge a x0 genera una successione f(xn) che converge a l=1.
Pertanto, il limite della funzione per x→0 è uguale a 1.
$$ \lim_{x \rightarrow 0} x^2+1 = 1 $$
L'infinito può essere un punto di accumulazione
Il punto di accumulazione può essere anche infinito (+∞ o -∞) per un insieme I⊆ R se in un intorno di infinito c'è almeno un punto di I.
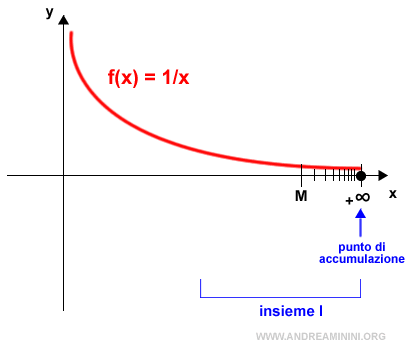
In questo caso l'intorno del punto di accumulazione x0 è un intervallo (M,+∞) che comprende ogni numero reale x>M.
Va da sé che +∞ è un punto di accumulazione soltanto se è l'estremo superiore di I.
Nota. Lo stesso si può dire per l'intorno (-∞, -M) per ogni x<-M. In questo caso, -∞ può essere un punto di accumulazione soltanto se è l'estremo inferiore di I.
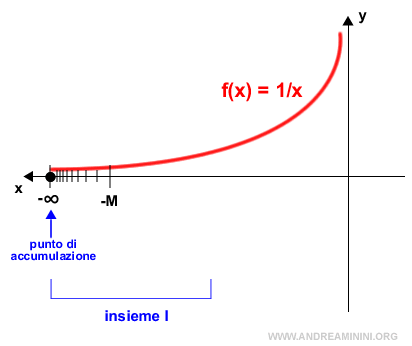
E così via.
