Come fare lo studio di una funzione

L'analisi di una funzione f(x) mi permette e disegnare il grafico della funzione tramite lo studio del dominio di definizione, del segno, delle derivate prime e seconde.

Ad esempio, ho la funzione f(x)

$$ f(x)= \frac{x}{x-1} $$

Per disegnare il grafico della funzione compio i seguenti passi.

Il dominio della funzione

Il primo passo dello studio di una funzione consiste nell'individuazione del dominio x ( campo di esistenza ) in cui la funzione è definita.

Nel caso della funzione f(x)=x/x-1 l'intervallo di definizione è

$$ ( -∞, 1) ∪ (1, ∞ ) \:\:\:\: \forall x \in R $$

Questo mi permette anche di trovare i punti in cui la funzione non è definita.

Ad esempio, la funzione f(x)=x/x-1 non è definita in x=1.

$$ f(1)= \frac{1}{1-1} |_{x=1} = \frac{1}{0} \:\:\: indefinita $$

Nei punti indefiniti potrebbero esserci degli asintoti verticali.

Lo studio del segno della funzione

Studio il segno della funzione f(x) nel campo di esistenza

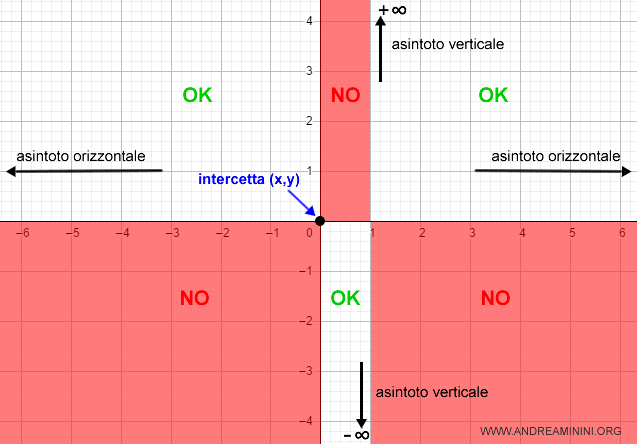
In questo caso la funzione è positiva nell'intervallo (-∞,0) e (1,∞) ed è negativa nell'intervallo ( 0, 1 )

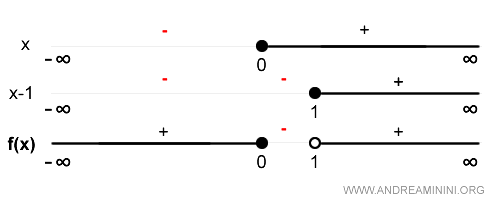
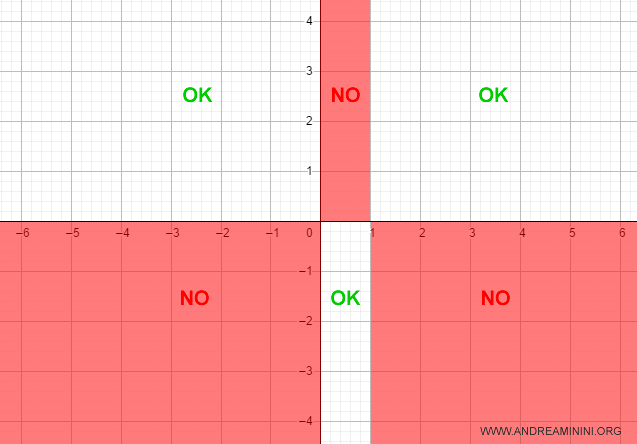
Lo studio del segno mi permette di capire in quali quadranti del diagramma cartesiano si presenta la funzione.

Tutti gli altri quadranti sono irrilevanti.

Gli asintoti orizzontali

Gli asintoti orizzontali si trovano calcolando il limite per x tendente a più o meno infinito agli estremi del campo di definizione della funzione.

$$ \lim_{x \rightarrow ∞}{ \frac{x}{x-1} } = \frac{∞}{∞} $$

$$ \lim_{x \rightarrow -∞}{ \frac{x}{x-1} } = \frac{∞}{∞} $$

I due limiti sono forme indeterminate.

Per risolverli utilizzo il teorema di L'Hopital.

$$ \lim_{x \rightarrow ∞}{ \frac{D[x]}{D[x-1]} } = \lim_{x \rightarrow ∞}{ \frac{1}{1} } = 1 $$

$$ \lim_{x \rightarrow -∞}{ \frac{D[x]}{D[x-1]} } = \lim_{x \rightarrow -∞}{ \frac{1}{1} } = 1 $$

Ora i limiti sono due numeri finiti.

Pertanto, per x tendente a +∞ e -∞ la funzione ha due asintoti orizzontali all'altezza delle ordinate y=1.

$$ \lim_{x \rightarrow ∞}{ \frac{x}{x-1} } = 1 $$

$$ \lim_{x \rightarrow -∞}{ \frac{x}{x-1} } = 1 $$

Li aggiungo al diagramma cartesiano

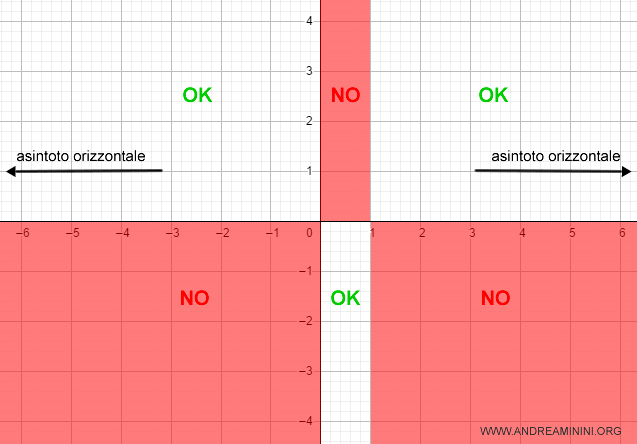
Gli asintoti verticali

Se nel dominio esistono dei punti indefiniti, calcolo il limite verso questi punti da destra e da sinistra.

In questo esempio la funzione non è definita nel punto x=1.

$$ \lim_{x \rightarrow 1^+}{ \frac{x}{x-1} } = \frac{1}{0^+} = ∞ $$

$$ \lim_{x \rightarrow 1^-}{ \frac{x}{x-1} } = \frac{1}{0^-} = -∞ $$

Pertanto, a destra di x=1 la funzione tende a +∞ mentre a sinistra di x=1 tende a -∞.

Aggiungo i due asintoti verticali al diagramma cartesiano.

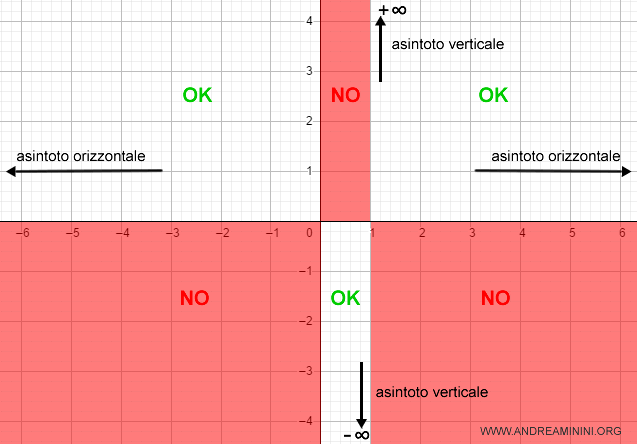
Gli asintoti obliqui

Se l'estremo è +∞ o -∞ posso verificare l'eventuale presenza di un asintoto obliquo mx+q calcolando i seguenti limiti

$$ m = \lim_{x \rightarrow ∞ } \frac{f(x)}{x} =\lim_{x \rightarrow ∞ } \frac{\frac{x}{x-1}}{x} = 0 $$

$$ q = \lim_{x \rightarrow ∞ } f(x)-mx = \lim_{x \rightarrow ∞ } \frac{x}{x-1} - 0 \cdot x = 1 $$

Se i limiti esistono e sono finiti, con m≠0, allora c'è un asintoto obliguo mx+q.

In questo caso, non esiste un asintoto obliquo né per +∞ che per -∞.

Nota. Nel caso della funzione f(x) il coefficiente angolare m=0 e q=1. Questo risultato coincide con gli asintoti orizzontali che ho già calcolato. Pertanto, non si tratta di asintoti obliqui.

Studio delle simmetrie

Verifico se la funzione gode di qualche simmetria.

Ad esempio se è una funzione pari

$$ f(-x)= f(x) $$

oppure una funzione dispari

$$ f(-x) = -f(x) $$

In questo caso, la funzione x/x-1 non è una funzione simmetrica.

Studio delle periodicità

Verifico se la funzione è periodica di periodo T.

$$ T: f(x+T)=f(x) \:\:\:\: \forall x \in R $$

Ad esempio, la funzione seno è una periodica per un periodo T=2π.

Se la funzione è periodica, basta studiarla in un solo periodo T e applicare il risultato dell'analisi in tutti gli altri periodi (T+1, T+2, ... ).

In questo caso specifico, la funzione x/x-1 non è una funzione periodica.

Le intercette con gli assi

Le intersezioni ( intercetta ) con gli assi x e y sono un'altra informazione utile per costruire il grafico.

Intercetta della f(x) con l'asse y

Ponendo x=0 calcolo il valore della y.

$$ y = \frac{x}{x-1}|_{x=0} = \frac{0}{0-1} = 0 $$

Quindi il punto di intersezione della funzione f(x) con l'asse y è il punto (0,0) ossia l'origine.

Intercetta della f(x) con l'asse x

Se non è troppo complesso, calcolo anche l'inverso.

Pongo y=0 per ottenere il valore della x.

$$ \frac{x}{x-1} = 0 $$

Nota. In questo caso specifico, l'intercetta con l'asse x coincide con l'intercetta con l'asse y, ossia con l'origine (0,0). Non è detto che sia sempre così. Le due intercette possono essere diverse o non esistere affatto.

Pertanto, la funzione passa sicuramente nel punto P(0,0).

Crescenza e decrescenza

Per individuare i tratti in cui la funzione è crescente o decrescente, calcolo la derivata prima della funzione

$$ f'(x) = D[ \frac{x}{x-1} ] = \frac{(x-1)-x}{(x-1)^2} = \frac{-1}{(x-1)^2} $$

Poi studio il segno della derivata prima.

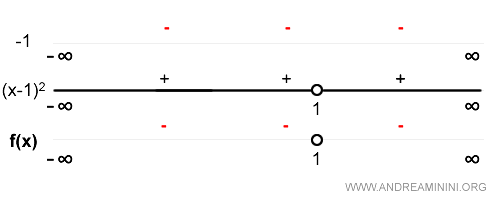
La funzione è crescente nei tratti in cui f'(x)>0 ed è decrescente nei tratti in cui f'(x)<0.

In questo caso la funzione è sempre decrescente in tutto il campo di definizione.

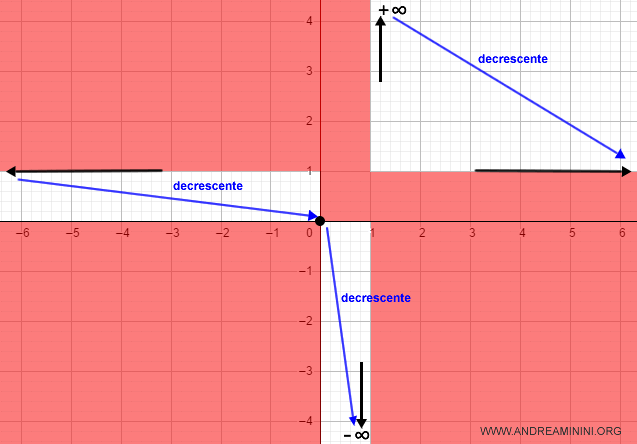
Nell'intervallo (-∞,0) la funzione decresce dall'asintoto orizzontale uguale a 1 fino all'intersezione O con gli assi.

Nell'intervallo (0, 1) la funzione passa per l'origine O e decresce verso infinito.

Nell'intervallo (1,∞) la funzione decresce dall'asintoto verticale fino all'asintoto orizzontale pari a 1.

Nota. Queste informazioni mi permettono di eliminare altre aree del diagramma cartesiano in cui sicuramente la funzione non esiste.

I minimi e massimi locali

Individuo i punti x0 in cui la derivata prima f'(x) è nulla per verificare l'esistenza di minimi e massimi locali.

$$ f'(x_0) = 0 $$

Nei punti in cui f'(x)=0 si trova un

• Massimo locale, se nell'intorno sinistro di x₀ la f(x) è crescente ( f'(x)>0 ) e nell'intorno destro la f(x) è decrescente ( f'(x)<0 ).
• Minimo locale, se nell'intorno sinistro di x₀ la f(x) è decrescente ( f'(x)<0 ) e nell'intorno destro la f(x) è crescente ( f'(x)>0 ).

In tutti gli altri casi, nel punto x₀ la funzione ha né un minimo, né un massimo.

Nel caso della funzione f'(x)=x/x-1 la derivata prima non è mai nulla.

$$ f'(x) = \frac{-1}{(x-1)^2} ≠ 0 \forall x \in R $$

Pertanto, non ci sono punti di minimo o massimo intermedi nell'intervallo di definizione.

I flessi ascendenti e discendenti

Analizzo i punti in cui la derivata prima della funzione è nulla.

$$ f'(x_0) = 0 $$

Nei punti in cui f'(x)=0 si trova un flesso se nell'intorno sinistro e destro di x₀ la f(x) è crescente ( f'(x)>0 ) o decrescente ( f'(x)<0 ).

Per capire se il flesso è ascendente o discendente occorre calcolare anche la derivata seconda della funzione.

Se la derivata seconda in x₀ è nulla. $$ f''(x_0) = 0 $$ In questo caso si rileva un

• Flesso ascendente se la derivata seconda f''(x) nell'intorno del punto x₀ passa da negativa a positiva (da concava a convessa).
• Flesso discendente se la derivata seconda f''(x) nell'intorno del punto x₀ passa da positiva a negativa (da convessa a concava).

In questo caso, la derivata prima della funzione non è mai nulla.

$$ f'(x) = \frac{-1}{(x-1)^2} ≠ 0 \forall x \in R $$

Quindi, non ci sono punti di flesso nell'intervallo di definizione.

La convessità e la concavità

A questo punto calcolo la derivata seconda della funzione f(x) per studiare i tratti in cui è concava o convessa.

$$ D^2[ f(x) ] = D[ \frac{-1}{(x-1)^2} ] = \frac{ 2(x-1)}{(x-1)^4} = \frac{2}{(x-1)^3} $$

Poi studio il segno della derivata seconda

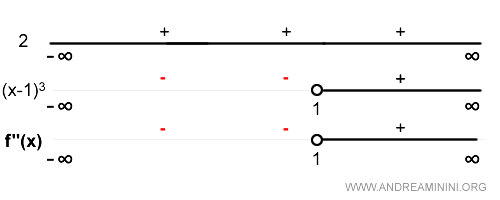
La funzione è

• convessa nei tratti in cui f"(x)≥0
• concava nei tratti in cui f"(x)≤0

Pertanto, la funzione f(x)=x/x-1 è concava nell'intervallo (-∞,1) e convessa nell'intervallo (1,∞).

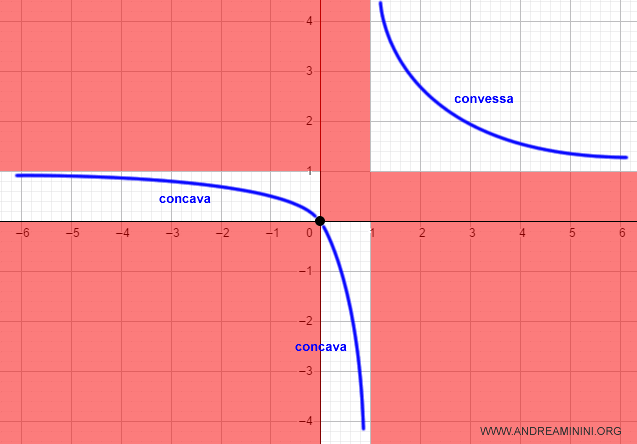
Ho così completato il grafico e lo studio della funzione.

E così via.