Il triangolo rettangolo
Il triangolo rettangolo è un triangolo con un angolo retto (90°).
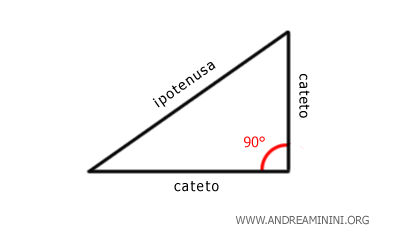
In un triangolo rettangolo i lati che formano l'angolo retto sono detti cateti.
Il lato opposto all'angolo retto è invece detto ipotenusa.
Il triangolo rettangolo è una delle figure geometriche più semplici ma è alla base di molti teoremi, della trigonometria e di numerose applicazioni pratiche.
L'interesse per il triangolo rettangolo risale alle antiche civiltà. Gli antichi egizi lo utilizzarono nella costruzione delle piramidi. Gli astronomi babilonesi utilizzavano tabelle trigonometriche nei loro calcoli celesti. Gli antichi greci, come Ipparco, svilupparono ulteriormente la trigonometria. Il greco Pitagora diede il suo nome a uno dei teoremi più conosciuti al mondo: il teorema di Pitagora.
Il teorema di Pitagora
In un triangolo rettangolo, la somma delle aree dei quadrati costruiti sui cateti è uguale all'area del quadrato costruito sull'ipotenusa.
$$ a^2 + b^2 = c^2 $$
Dove "a" e "b" sono le lunghezze dei cateti, mentre "c" è la lunghezza dell'ipotenusa.
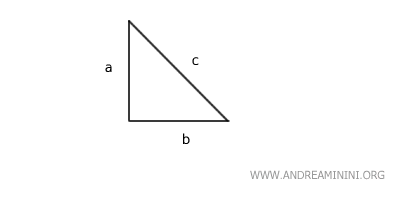
Detto in altri termini, il quadrato costruito sull'ipotenusa è uguale alla somma dei quadrati costruiti sui cateti.
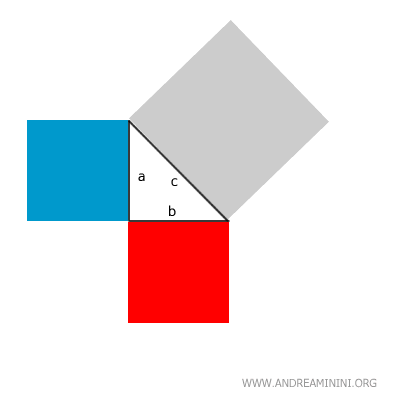
Da questo si deduce che l'ipotenusa è sempre il lato più lungo in un triangolo rettangolo.
Mettendo sotto radice quadrata entrambi i membri
$$ \sqrt{c^2} = \sqrt{a^2 + b^2} $$
Poi semplificando, ottengo la formula più conosciuta del teorema:
$$ c = \sqrt{a^2 + b^2} $$
Questa formula ha rivoluzionato la geometria e, ancora oggi, ha applicazioni in diversi altri campi della conoscenza, dalla fisica alla navigazione. Ad esempio, è utilizzata per calcolare la distanza tra due punti.
L'altezza di un triangolo rettangolo rispetto all'ipotenusa
L'altezza di un triangolo rettangolo rispetto all'ipotenusa è uguale al prodotto dei cateti (a×b) diviso l'ipotenusa (c) $$ h = \frac{a \times b}{c} $$ dove \( a \) e \( b \) sono le lunghezze dei cateti, e \( c \) è la lunghezza dell'ipotenusa.

Questo risultato deriva dal fatto che l'area del triangolo può essere espressa in modi diversi.
Esempio
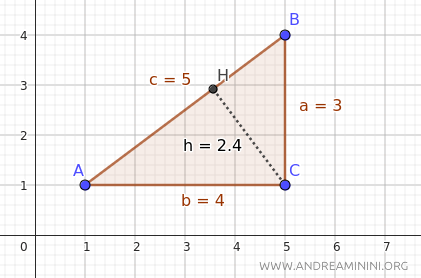
Prendo come esempio questo triangolo rettangolo di cui conosco tutte le lunghezze dei lati.
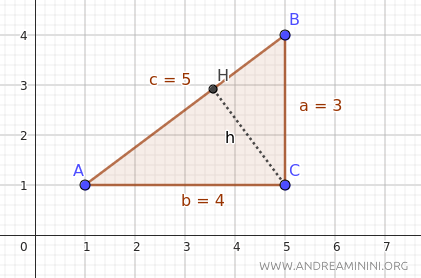
Voglio calcolare l'altezza (h) rispetto all'ipotenusa (c).
Per farlo applico la formula seguente:
$$ h = \frac{a \times b}{c} $$
In questo caso i cateti misurano a=3, b=4 e l'ipotenusa c=5.
$$ h = \frac{3 \times 4}{5} $$
$$ h = \frac{12}{5} $$
$$ h = 2.4 $$
L'altezza rispetto all'ipotenusa misura circa h=2.4.
Il risultato è corretto come dimostra anche la verifica fatta su Geogebra.
Dimostrazione
Cerco di dimostrare la formula dell'altezza rispetto all'ipotenusa
$$ h = \frac{a \times b}{c} $$
In generale, l'altezza (h) di un triangolo (anche non rettangolo) rispetto a qualsiasi lato preso come base si ottiene applicando questa formula.
$$ h = \frac{2 \cdot A}{\text{base}} $$
Dove A è l'area del triangolo mentre "base" è la lunghezza di un lato preso come base.
L'area di un triangolo rettangolo, invece, è uguale al semiprodotto tra la base per l'altezza.
$$ A = \frac{\text{base} \times \text{altezza}}{2} $$
Nel triangolo rettangolo posso prendere come "base" un cateto e come "altezza" l'altro cateto.

Quindi, l'area del triangolo diventa $ A=\frac{a \cdot b}{2} $
Sostituisco l'area A nella formula iniziale e semplifico
$$ h = \frac{2 \cdot A}{\text{base}} $$
$$ h = \frac{2 \cdot ( \frac{a \cdot b}{2} )}{\text{base}} $$
$$ h = \frac{a \cdot b}{\text{base}} $$
Ora considero come base l'ipotenusa (c).
$$ h = \frac{a \cdot b}{\text{c}} $$
E in questo modo ottengo la formula che volevo dimostrare.
L'altezza (h) di un triangolo rettangolo rispetto all'ipotenusa è uguale al prodotto dei cateti diviso l'ipotenusa.
Questo risultato è particolarmente utile in contesti di geometria più avanzata. Ad esempio, in geometria analitica l'ho usato per dimostrare la distanza di un punto da una retta sul piano cartesiano.
Dimostrazione alternativa. Per dimostrare che l'altezza \( h \) di un triangolo rettangolo rispetto all'ipotenusa è uguale al prodotto dei cateti diviso per l'ipotenusa, posso anche usare la relazione tra l'area del triangolo espressa in due modi diversi. Considero un triangolo rettangolo con cateti di lunghezza \( a \) e \( b \), e ipotenusa \( c \). L'area \( A \) del triangolo può essere espressa come metà del prodotto dei cateti: $$ A = \frac{1}{2}ab $$ L'area \( A \) del triangolo posso esprimerla anche come metà del prodotto dell'ipotenusa \( c \) e l'altezza \( h \) relativa all'ipotenusa: $$ A = \frac{1}{2}ch $$ Poiché entrambe le espressioni rappresentano l'area dello stesso triangolo, possiamo eguagliarle: $$ \frac{1}{2}ab = \frac{1}{2}ch $$ A questo punto semplifico la frazione cancellando \( \frac{1}{2} \) da entrambi i lati dell'equazione e risolvendo per \( h \). $$
ab = ch $$ Da cui ricavo l'altezza (h) $$ h = \frac{ab}{c} $$ Questo dimostra che l'altezza \( h \) relativa all'ipotenusa è effettivamente il prodotto dei cateti diviso per l'ipotenusa.
Criteri di congruenza del triangolo rettangolo
Il triangolo rettangolo gode di criteri di congruenza specifici:
- Due triangoli rettangoli sono congruenti se hanno i cateti congruenti
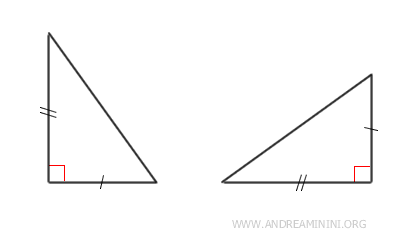
Dimostrazione. In base al primo principio di congruenza (LAL) due triangoli sono congruenti se hanno due lati congruenti e l'angolo tra di essi congruente. In un triangolo rettangolo l'angolo tra i due cateti è sempre un angolo retto (90°). Quindi è un dato noto. Pertanto, il criterio di congruenza tra due triangoli rettangoli si riduce al fatto che ci siano due cateti congruenti.
- Due triangoli rettangolo sono congruenti se hanno un lato e un angolo acuto congruente
Dimostrazione. I triangoli rettangolo hanno un angolo retto, quindi se un angolo acuto è congruente anche l'ultimo angolo è congruente perché la somma degli angoli interni è sempre 180°. Sapendo che un lato è congruente per l'ipotesi iniziale, per il secondo principio di congruenza generalizzato (ALA) i due triangoli sono congruenti.
- Due triangoli rettangolo sono congruenti se hanno ordinatamente un cateto e l'ipotenusa congruenti
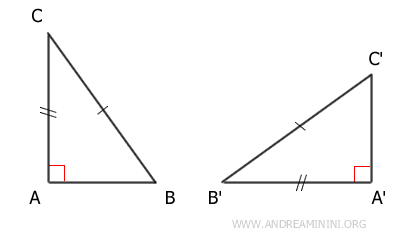
Dimostrazione. Per l'ipotesi iniziale due triangoli ABC e A'B'C' hanno un cateto AC≅A'B' e l'ipotenusa congruenti BC≅B'C'. A questo punto costruisco un triangolo ACD≅A'B'C' congruente con il triangolo A'B'C' e che condivide il cateto AC in comune con il triangolo ABC.
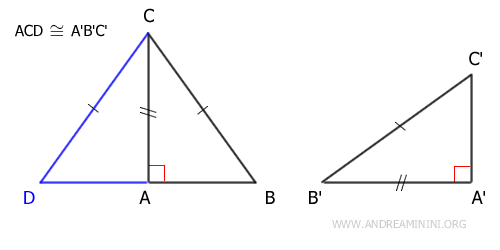
Il triangolo BCD è un triangolo isoscele perché ha due lati congruenti BC≅CD. Essendo un triangolo isoscele ha anche gli angoli acuti adiacenti alla base congruenti β≅γ.
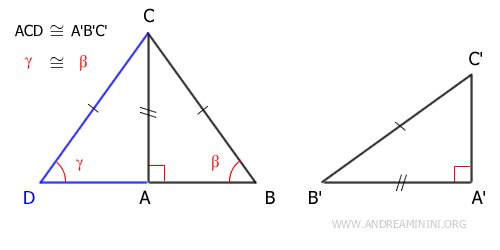
A questo punto per il secondo principio di congruenza generalizzato (ALA) i due triangoli ACD≅ABC sono congruenti perché hanno un lato coincidente AC, un lato congruente BC≅CD e un angolo congruente β≅γ. Di conseguenza, sapendo che ACD≅A'B'C' sono congruenti per costruzione, posso dedurre tramite la proprietà transitiva che anche i triangoli ABC≅A'B'C' congruenti.
Dimostrazione alternativa
Per ipotesi iniziale ho due triangoli rettangoli ABC e A'B'C' con angoli retti al vertice B e B', un cateto congruente BC=B'C' e l'ipotenusa congruente AC=A'C'. Devo dimostrare che i triangoli ABC≅A'B'C' sono congruenti (tesi).
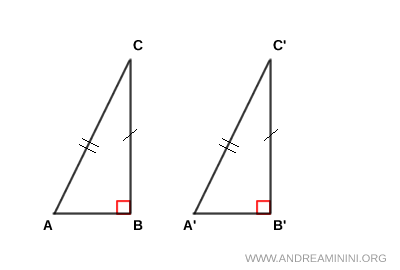
Prolungo il segmento A'B' con un segmento congruente B'D≅AB e congiungo il punto D con C'. In questo modo ottengo un triangolo B'C'D. Poiché l'angolo al vertice B' è supplementare a un angolo retto, è anch'esso un angolo retto. Quindi, il triangolo B'C'D è un altro triangolo rettangolo.
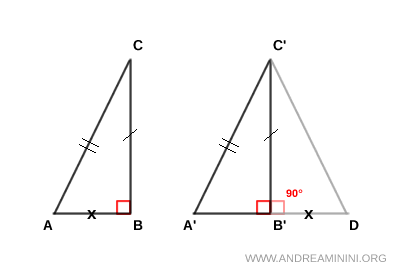
Per il primo criterio di congruenza (LAL) i triangoli ABC e B'C'D sono congruenti ABC≅B'C'D perché hanno un lato congruenti AB≅B'D per costruzione, un lato congruente BC≅B'C' per ipotesi iniziale e l'angolo retto (90°) tra di essi congruente. Quindi, i lati AC≅C'D sono congruenti.
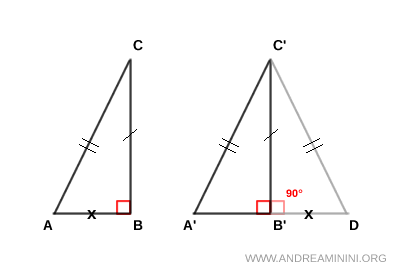
Il triangolo A'C'D è isoscele perché ha i due lati obliqui congruenti. Essendo congruenti, l'altezza B'C' del triangolo isoscele coincide con la mediana, quindi i segmenti A'B' ≅B'D sono congruenti.
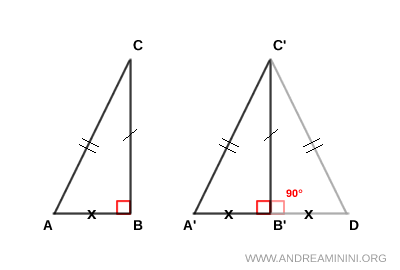
Di conseguenza i triangoli A'B'C'≅B'C'D sono congruenti per il terzo criterio di congruenza (LLL) perché hanno tutti i lati congruenti. Quindi, sapendo che ABC≅B'C'D e A'B'C'≅B'C'D, per la proprietà transitiva sono congruenti anche i triangoli ABC≅A'B'C' come volevasi dimostrare.
Il triangolo rettangolo e la trigonometria
In trigonometria il triangolo rettangolo gioca un ruolo centrale.
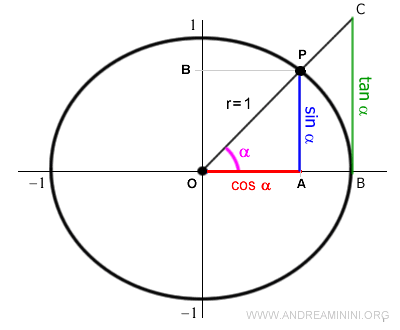
Tutte le principali funzioni trigonometriche sono, in qualche modo, legate al triangolo rettangolo.
- Seno
Il seno è definito come il rapporto tra il cateto opposto all'angolo α e l'ipotenusa. $$ \sin ( \alpha ) = \frac{AP}{OP} $$ - Coseno
Il coseno è definito come il rapporto tra il cateto adiacente all'angolo α e l'ipotenusa. $$ \sin ( \alpha ) = \frac{OA}{OP} $$ - Tangente
La tangente è definita come il rapporto tra il cateto opposto e il cateto adiacente all'angolo α. $$ \tan( \alpha) = \frac{AP}{OA} = \frac{\sin( \alpha )}{\cos( \alpha } $$
Prendendo un angolo acuto del triangolo (diverso dall'angolo retto), i lati del triangolo possono essere direttamente correlati a queste funzioni.
La trigonometria ha innumerevoli applicazioni pratiche
Ad esempio, è usata nella navigazione per calcolare le distanze, in architettura per la progettazione degli edifici, in elettronica nello studio delle onde, ecc.
Pertanto, il triangolo rettangolo è forse una delle figure geometriche più vicine alla nostra vita quotidiana.
Osservazioni
Alcune osservazioni e note sul triangolo rettangolo.
- Ortocentro
In un triangolo rettangolo l'ortocentro coincide con il vertice che corrisponde all'angolo retto.
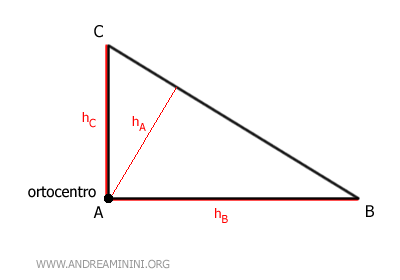
- In un triangolo rettangolo gli angoli acuti sono angoli complementari
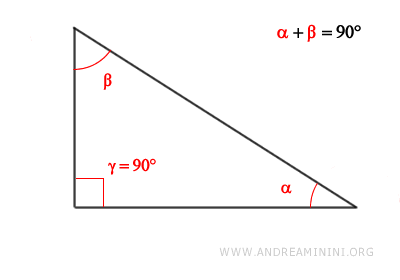
Dimostrazione. Un triangolo rettangolo ha un angolo retto (90°). Per il teorema della somma degli angoli interni, la somma degli angoli interni di un triangolo è congruente a un angolo piatto (180°) $$ \alpha + \beta + \gamma = 180° $$ Sapendo che un angolo è un angolo retto, ad esempio γ =90° $$ \alpha + \beta + \gamma = 180° $$ $$ \alpha + \beta + 90° = 180° $$ $$ \alpha + \beta = 180° - 90° $$ $$ \alpha + \beta = 90° $$ Pertanto, gli angoli acuti del triangolo sono angoli complementari ossia la loro somma è congruente a un angolo retto.
- In un triangolo rettangolo la mediana dell'ipotenusa è congruente alla metà dell'ipotenusa
In un triangolo rettangolo la lunghezza della mediana (AM) applicata all'ipotenusa (BC) è uguale alla metà della lunghezza dell'ipotenusa (AM≅1/2 BC).
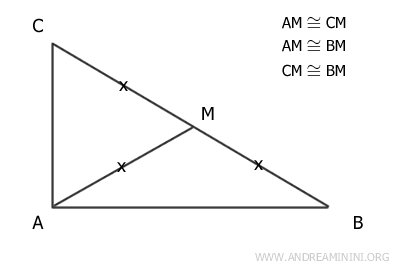
Vale anche il teorema inverso, se in un triangolo una mediana è la metà del lato a cui è applicata, allora il triangolo è rettangolo.
Dimostrazione. Per ipotesi iniziale considero un triangolo rettangolo ABC, il punto medio M dell'ipotenusa e la mediana rispetto all'ipotenusa. Di conseguenza so per certo che l'angolo α è un angolo retto (α=90°) e i segmenti BM≅CM sono congruenti perché M è il punto medio dell'ipotenusa AB.
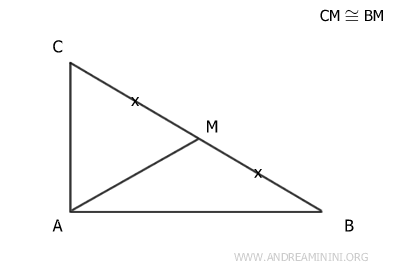
A questo punto prolungo il segmento AM con un segmento congruente MD. Poi traccio i segmenti BD e CD. In questo modo ottengo un quadrilatero.
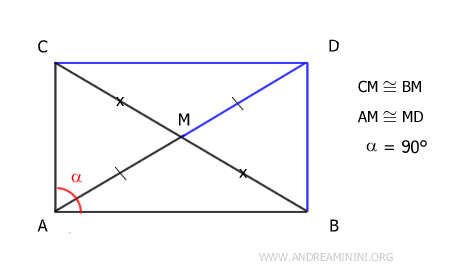
Deduco che il quadrilatero è un parallelogramma perché le sue diagonali AD e BC si incontrano nel loro punto medio. Inoltre, sapendo che l'angolo α=90° per l'ipotesi iniziale (triangolo rettangolo), deduco che il parallelogramma sia anche un rettangolo. In un rettangolo le diagonali sono congruenti AD≅BC. Quindi, sono congruenti anche le metà dei segmenti AD/2≅BC/2 ossia AM≅BM e AM≅CM. Questo dimostra che in un triangolo rettangolo la mediana rispetto all'iponenusa AM è congruente con la metà dell'ipotenusa ossia AM≅CM e AM≅BM.
Dimostrazione alternativa. Considero un triangolo rettangolo e il punto medio M dell'ipotenusa (AC). Quindi, BM è la mediana dell'ipotenusa.
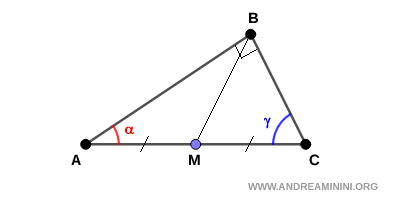
Prolungo la mediana BM di un segmento BD≅BM di pari lunghezza. Poi traccio il segmento AD e ottengo un altro triangolo ABD.
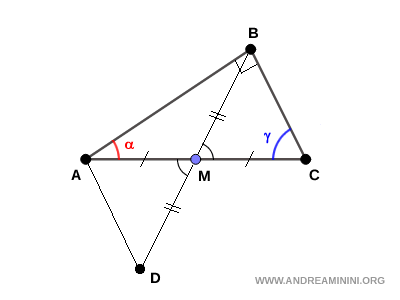
I triangoli ADM≅BCM sono congruenti per il primo criterio di congruenza (LAL) perché hanno due lati congruenti (AM≅CM per ipotesi iniziale e BD≅BM per costruzione) e l'angolo tra di essi congruente $ A \hat{M}D≅B \hat{M} C $, in quanto sono angoli opposti allo stesso vertice (M). Essendo congruenti, hanno gli angoli e i lati congruenti nello stesso ordine. In particolar modo mi interessa sapere che $ \alpha' \cong \gamma $.
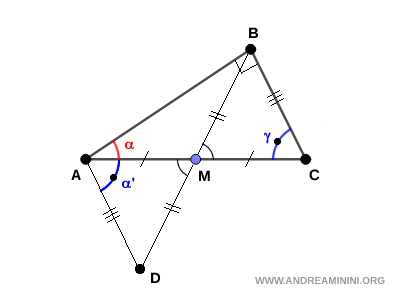
Dal triangolo ABC so che gli angoli α e γ sono complementari $$ \alpha + \gamma = 90° $$ Sapendo che α'≅γ allora anche α e α' sono complementari $$ \alpha + \alpha' = 90° $$ Pertanto, il triangolo ABD è un triangolo rettangolo. I triangoli ABD≅ABC sono congruenti perché hanno i cateti congruenti (AB in comune e AD≅BC). Quindi, anche le loro ipotenuse sono congruenti $$ AC \cong BD $$ Sapendo che $ BD = 2 BM $ per costruzione $$ AC \cong 2 BM $$ Pertanto, la mediana (BM) è la metà dell'ipotenusa (AC) del triangolo ABC. $$ BM \cong \frac{1}{2} AC $$ Come volevasi dimostrare.
Dimostrazione del teorema inverso. Considero un triangolo ABC in cui la mediana BM è uguale alla metà del lato AC a cui è applicata.
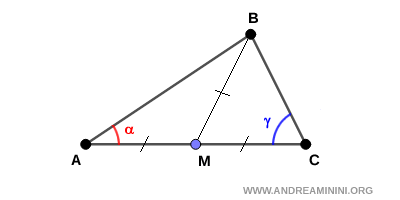
Questo significa che $$ BM = \frac{1}{2} AC $$ I segmenti BM, AM e CM sono congruenti $$ BM \cong AM \cong CM $$ I triangoli ABM e BCM sono isosceli perché hanno due lati congruenti (BM=AM) e (BM=AC). Quindi, gli angoli alla base sono congruenti in ciascun triangolo isoscele ABM e BCM.
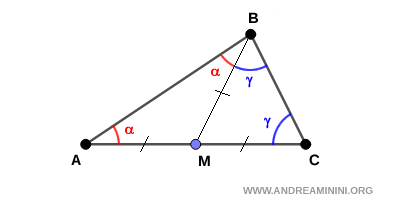
Sapendo che la somma degli angoli interni di un triangolo è sempre 180°, la somma degli angoli interni del triangolo ABC è $$ \alpha + \gamma + (\alpha + \gamma) = 180° $$ $$ 2\alpha + 2\gamma = 180° $$ Divido per due entrambi i membri dell'equazione $$ \alpha + \gamma = 90° $$ Quindi, l'angolo restante del triangolo ABC è un angolo retto. Pertanto, il triangolo ABC è un triangolo rettangolo, come volevasi dimostrare. - Il caso del triangolo rettangolo con gli angoli acuti di 30° e 60°
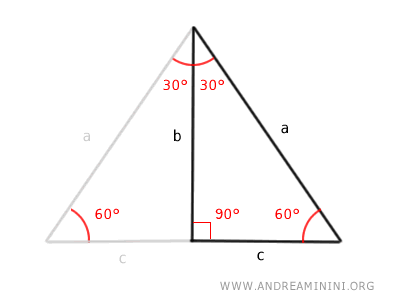
Un triangolo rettangolo con gli angoli acuti di 30° e 60° è la metà di un triangolo equilatero. Questo mi permette di calcolare la lunghezza di tutti i lati del triangolo a partire dalla lunghezza di un solo lato. $$ a = \frac{2b}{\sqrt{3}} $$ $$ b = \frac{a}{2} \sqrt{3} $$ $$ c = \frac{a}{2} $$ Queste formule si applicano soltanto ai triangoli con angoli interni pari a 30°, 60° e 90°. - Il caso del triangolo rettangolo con due angoli acuti di 45° e 45° (triangolo rettangolo isoscele)
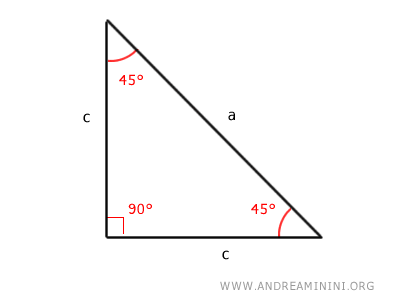
Questo particolare tipo di triangolo rettangolo è anche un triangolo isoscele perché ha i due cateti congruenti (c). Questo mi permette di conoscere la lunghezza di tutti i lati del triangolo a partire da un solo lato. $$ c = \frac{a}{ \sqrt{2} } $$ $$ a = c \cdot \sqrt{2} $$ Queste formule si applicano solo ai triangoli con due angoli acuti di 45°. - Due triangoli rettangoli sono simili se hanno i cateti in proporzione
In base al secondo criterio di similitudine dei triangoli, due triangoli sono simili se hanno i lati ordinatamente proporzionali e l'angolo tra di essi congruente.
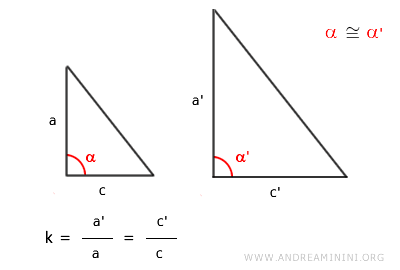
Nei triangoli rettangoli l'angolo tra i cateti è sempre un angolo retto (90°), quindi è congruente. Quindi, se i cateti sono in proporzione, per il secondo criterio di similitudine i due triangoli sono triangoli simili ovvero hanno tutti gli angoli congruenti, la stessa forma ma la dimensione e l'orientamento che può essere differente. - Due triangoli rettangoli con un angolo acuto congruente sono simili
La somma degli angoli interni di un triangolo è sempre 180°. $$ \alpha + \beta + \gamma = 180° $$ Sapendo che in due triangoli rettangoli l'angolo retto è 90°, se hanno anche un angolo acuto congruente, allora per differenza anche il terzo angolo è congruente. Pertanto, i due triangoli hanno tutti gli angoli ordinatamente congruenti e, in base al primo principio di similitudine dei triangoli, i due triangoli sono simili.
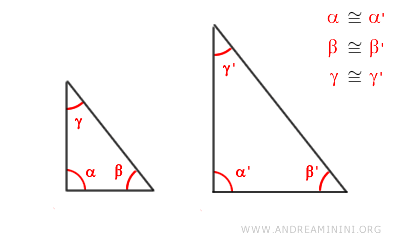
E così via.
