La similitudine

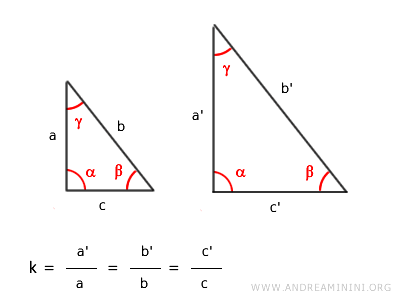
La similitudine è un tipo di affinità che conserva la forma della figura, mantenendo la congruenza degli angoli e un rapporto di proporzionalità costante $ k $ tra i lati corrispondenti. E' una trasformazione geometrica che si può ottenere tramite la composizione di una omotetia e una isometria.

In genere si indica una similitudine con la lettera greca sigma minuscola $ \sigma $.

Si tratta di una trasformazione geometrica che mantiene la forma ma non le dimensioni.

In altre parole, due figure sono dette figure simili se si corrispondono in una similitudine, ovvero se hanno:

1. Gli angoli corrispondenti sono congruenti, cioè di uguale ampiezza
2. i lati corrispondenti sono proporzionali, e il rapporto di similitudine $ k $ è lo stesso per tutte le coppie di lati corrispondenti

Questo equivale a dire che una figura simile a un'altra mantiene la stessa forma ma modifica le sue dimensioni.

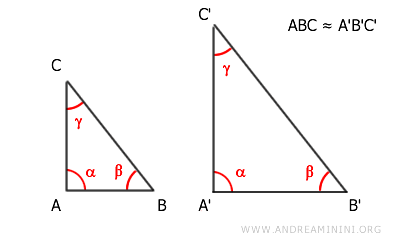
Il simbolo della similitudine sono due onde sovrapposte "≈".

Ad esempio, per indicare che le figura ABC e A'B'C' sono simili scrivo:

$$ ABC ≈ A'B'C' $$

I lati e gli angoli che si corrispondono in una similitudine sono detti lati omologhi e angoli omologhi.

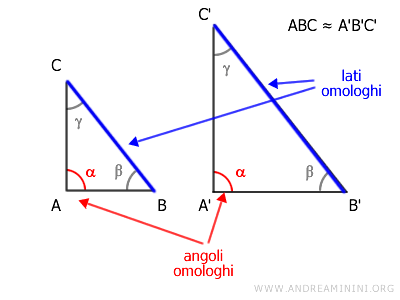
Nota. Nei due triangoli simili, i lati omologhi sono quelli che si trovano in posizione opposta rispetto agli angoli congruenti dei due triangoli. In altre parole, i lati omologhi sono i lati opposti agli angoli congruenti.

Il rapporto di proporzionalità (k) è lo stesso per tutti i lati omologhi ed è detto anche rapporto di similitudine o rapporto di scala.

Pertanto, gli invarianti di una similitudine sono le ampiezze degli angoli e i rapporti fra i segmenti corrispondenti omologhi.

• Conserva il rapporto fra le lunghezze.
• Conserva l'ampiezza degli angoli perché trasforma un angolo in un angolo congruente.
• Se due rette sono perpendicolari nella figura origi, restano perpendicolari anche nella figura simile. Lo stesso accade se sono parallele, queste restano parallele.

Quindi, la similitudine preserva il parallelismo: se due lati di una figura sono paralleli, allora i lati corrispondenti della figura simile risultano anch’essi paralleli (affinità).

Un esempio pratico di similitudine è la riproduzione di una fotografia in un formato più grande rispetto all'originale. Ad esempio, ingrandire una foto per metterla in una cornice. La foto originale e quella ingrandita hanno la stessa forma ma dimensioni diverse.

In modo analogo la similitudine si estende anche nello spazio a tre dimensioni tra i solidi che hanno gli angoli corrispondenti congruenti e hanno i segmenti corrispondenti paralleli (affinità spaziale) con lo stesso rapporto di proporzionalità |k|.

Il rapporto di similitudine

Quando due figure sono simili, le loro corrispondenti lunghezze dei lati sono in proporzione, e questa proporzione è chiamata il fattore di scala della similitudine o rapporto di similitudine. Il rapporto di similitudine è sempre positivo ( $ k > 0 $ ).

• Ingrandimento (k>1)
  Se il rapporto di similitudine è maggiore di 1 la figura risulta ingrandita in scala 1:k.

  
  Ad esempio, se k=2 la figura è ingrandita in una scala 1:2. Se il fattore di scala è 2, tutte le lunghezze nella figura simile sono il doppio di quelle nella figura originale.

• Isometria (k=1)
  Se il rapporto di similitudine è uguale a 1 la trasformazione geometrica rientra nelle isometrie (es. rotazioni, traslazioni, riflessioni, ecc.)
  
• Riduzione (0<k<1)
  Se il rapporto di similitudine è compreso tra 0 e 1, la figura risulta ridotta in scala 1:k.
  

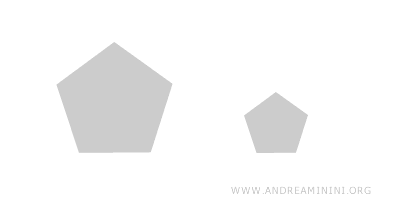
  Ad esempio, se k=0.5 la figura è ridotta in scala 1:0.5 ovvero, in modo del tutto equivalente, in scala 2:1

In tutti i casi le figure simili mantengono la stessa forma.

Poligoni simili

Due poligoni sono simili se hanno i lati corrispondenti in proporzione costante e gli angoli corrispondenti della stessa ampiezza (angoli corrispondenti congruenti).

In generale, tutti i poligoni regolari e i cerchi sono simili tra loro.

I criteri di similitudine del triangolo

Ci sono alcuni criteri principali che stabiliscono la similitudine tra due figure geometriche. In particolare tra i triangoli.

• Criterio AAA (Angolo-Angolo-Angolo)
  Due triangoli sono simili se hanno corrispondenti angoli congruenti.
  

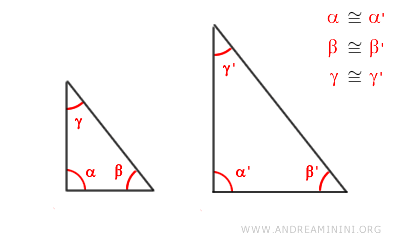
  Nota. In realtà, per determinare la similitudine tra due triangoli basta che ci siano due angoli corrispondenti congruenti. Se due triangoli hanno due angoli congruenti, allora anche il terzo angolo sarà congruente a causa della proprietà che la somma degli angoli interni in un triangolo è sempre uguale a 180 gradi.

• Criterio LAL (Lato-Angolo-Lato)
  Due triangoli sono simili se due lati di un triangolo sono proporzionali ai due corrispondenti lati dell'altro triangolo, e l'angolo compreso tra i due lati è uguale in entrambi i triangoli.
  
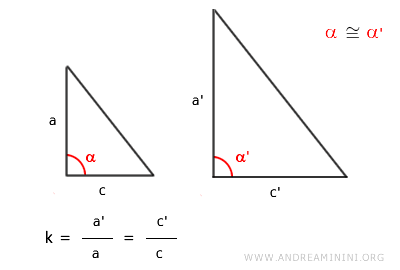
• Criterio LLL (Lato-Lato-Lato)
  Due triangoli sono simili se i lati di uno sono proporzionali ai corrispondenti lati dell'altro triangolo. Questo significa che tutte le lunghezze dei lati di un triangolo sono in uno stesso rapporto costante con le lunghezze dei lati corrispondenti dell'altro triangolo.
  

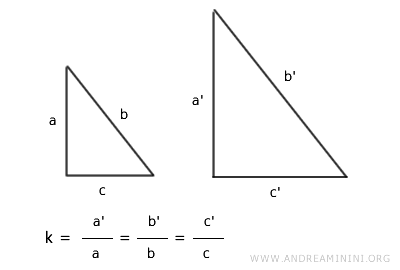
Le equazioni della similitudine

La similitudine posso rappresentarla nel piano cartesiano Oxy tramite questo sistema di equazioni in forma matriciale.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = M \cdot \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} c \\ d \end{pmatrix} $$

Dove la matrice M cambia a seconda se si tratta di una similitudine diretta o invertente

• Similitudine diretta $$ M =  \begin{pmatrix} a & -b \\ b &a \end{pmatrix} $$
• Similitudine invertente $$ M =  \begin{pmatrix} a & b \\ b & -a \end{pmatrix} $$

Quindi, nel caso di una similitudine diretta il sistema di equazioni cartesiane è il seguente:

$$ \begin{cases} x' = ax-by  + c  \\ \\ y' = bx+ay +d \end{cases} $$

Nella similitudine inversa, invece, il sistema di equazioni cartesiane è il seguente:

$$ \begin{cases} x' = ax+by  + c  \\ \\ y' = bx-ay +d \end{cases} $$

In entrambi i casi il rapporto di similitudine k è il seguente:

$$ k = \sqrt{a^2+b^2} $$

In alternativa, posso rappresentare la similitudine anche in questa forma trigonometrica: $$ \begin{cases} x' = k \cdot ( x \cos \alpha \pm y \sin \alpha ) \\ \\ y' = k \cdot ( x \sin \alpha \pm y \cos \alpha ) \end{cases} $$

Esempio

Considero questa trasformazione geometrica.

\[ \tau:\; \begin{cases} x' = 2x + y + 1 \\ \\ y' = x - 2y - 1 \end{cases} \]

La matrice dei coefficienti del sistema è

\[ A= \begin{pmatrix} 2 & 1\\ 1 & -2 \end{pmatrix} \]

Quindi, si tratta di una similitudine indiretta perché la matrice ha la forma \(\begin{pmatrix} a & b \\ b & -a \end{pmatrix}\) con \(a=2\) e \(b=1\).

Calcolo il determinante della matrice $ A $

\[ \det A= \det \begin{pmatrix} 2 & 1\\ 1 & -2 \end{pmatrix} = (2)(-2) - (1)(1) = -4 - 1 = -5 \]

Il determinante della parte lineare è negativo, quindi l’orientamento viene invertito.

Infine, calcolo il rapporto di scala della similitudine:

\[ k=\sqrt{a^2+b^2}=\sqrt{2^2+1^2}=\sqrt{5} \]

Pertanto, la trasformazione \(\tau\) è una similitudine indiretta con rapporto \(k=\sqrt{5}\). Questo valore $ k $ moltiplica tutte le lunghezze.

A questo punto, applico la trasformazione \(\tau\) a un triangolo rettangolo isoscele \(OAB\) con i vertici alle coordinate \(\,O(0,0),\;A(1,0),\;B(0,1)\).

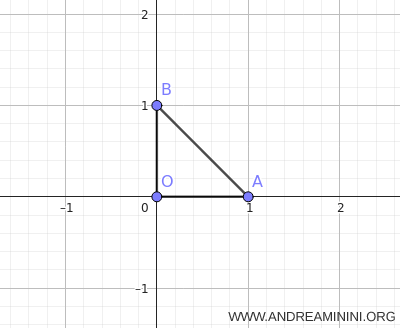
Calcolo le immagini dei tre vertici usando le equazioni di \(\tau\).

• Punto \(O\):
  Calcolo le coordinate del punto $ O' $ dopo la trasformazione \[ x'_O = 2\cdot 0 + 0 + 1 = 1,\qquad y'_O = 0 - 2\cdot 0 - 1 = -1 \] Quindi, il nuovo punto si trova alle coordinate \( O'(1,-1) \).
• Punto \(A\):
  Calcolo le coordinate del punto $ A' $ dopo la trasformazione \[ x'_A = 2\cdot 1 + 0 + 1 = 3,\qquad y'_A = 1 - 2\cdot 0 - 1 = 0 \] Le coordinate del nuovo punto sono \( A'(3,0) \).
• Punto \(B\)
  Calcolo le coordinate del punto $ B' $ dopo la trasformazione \[ x'_B = 2\cdot 0 + 1 + 1 = 2,\qquad y'_B = 0 - 2\cdot 1 - 1 = -3 \] Il nuovo punto si trova alle coordinate \( B'(2,-3) \).

Spiegazione. Per calcolare le coordinate $ (x',y') $ della figura trasformata, sostituisco le coordinate $ (x,y) $ di partenza di ogni punto nel sistema di equazioni della trasformazione. Ad esempio, per il punto \( O = (0,0) \). \[ \tau:\; \begin{cases} x' = 2x + y + 1 \\ \\ y' = x - 2y - 1 \end{cases} \] Sostituisco $ x=0 $ e $ y=0 $ \[ \tau:\; \begin{cases} x' = 2 \cdot 0 + 0 + 1 \\ \\ y' = 0 - 2 \cdot 0 - 1 \end{cases} \] \[ \tau:\; \begin{cases} x' = 1 \\ \\ y' = - 1 \end{cases} \] Le coordinate del punto trasformato sono $ O'(1,-1) $.

Quindi, dopo la trasformazione ottengo il triangolo $ O'A'B' $ che ha per vertici i punti $ O'(1,-1) $,  $ A'(3,0) $, $ B'(2,-3) $.

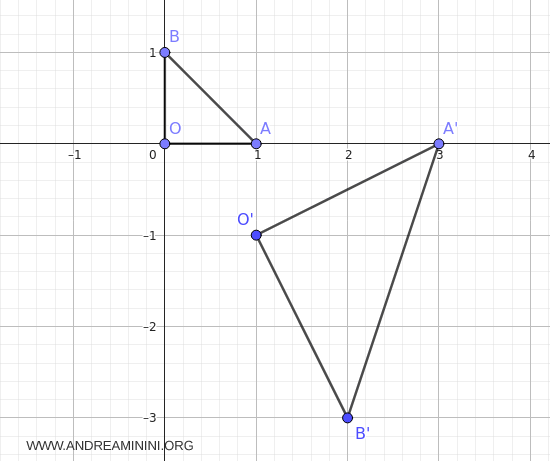
Nel triangolo di partenza $ OAB $ le lunghezze dei lati erano \(\overline{OA}=1\), \(\overline{OB}=1\), \(\overline{AB}=\sqrt{2}\).

Nel triangolo trasformato $ O'A'B' $ tramite la similitudine con rapporto \(k =\sqrt{5} \) le lunghezze dei lati sono moltiplicate per $ k $:

• \( O'A'= k \cdot OA = \sqrt{5} \cdot 1 = \sqrt{5}\)
• \( O'B' = k \cdot OB = \sqrt{5} \cdot 1 = \sqrt{5}\)
• \( A'B' = k \cdot AB = \sqrt{5} \cdot 2 =  \sqrt{10}\)

In conclusione, tutte le lunghezze vengono moltiplicate per \(\sqrt{5}\), l’orientamento della figura viene invertito, mentre angoli e proporzioni rimangono invariati. Il triangolo trasformato resta comunque un triangolo rettangolo e isoscele.

Similitudine nello spazio

La similitudine nello spazio è definita in modo analogo alla similitudine nel piano.

Si tratta di una trasformazione geometrica ottenuta dalla composizione di un'isometria (cioè una trasformazione che conserva le distanze, come traslazioni, rotazioni e riflessioni) e di un'omotetia (cioè una trasformazione che dilata o riduce un oggetto mantenendo inalterate le sue proporzioni).

Le proprietà della similitudine nello spazio

La similitudine ha le seguenti proprietà:

• Mantiene invariati gli angoli tra gli elementi geometrici.
• Trasforma i segmenti in segmenti proporzionali, mantenendo il rapporto di similitudine costante.
• Il rapporto di similitudine è lo stesso rapporto di omotetia e determina l'entità della trasformazione.

Esempi concreti di similitudine spaziale

Se una struttura viene scalata con un rapporto di similitudine \( k = 2 \), allora tutte le lunghezze, le altezze e le profondità della nuova struttura saranno raddoppiate rispetto all’originale.

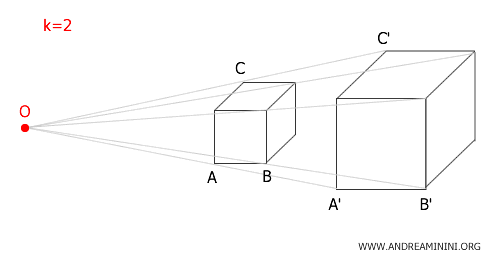
Viceversa, se un solido viene trasformato con un rapporto di similitudine \( k = \frac{1}{2} \), allora il nuovo solido avrà spigoli della metà della lunghezza rispetto all’originale, ma manterrà la stessa forma.

Osservazioni

Alcune osservazioni e note a margine sulla similitudine

• La similitudine è equivalente alla composizione di una omotetia e una isometria
  Nel piano la similitudine equivale a una composizione geometrica di una omotetia e una isometria (traslazione, rotazione, simmetria centrale o assiale, identità), o viceversa. Ecco un esempio pratico di prodotto di un'omotetia e di una isometria.
  
  
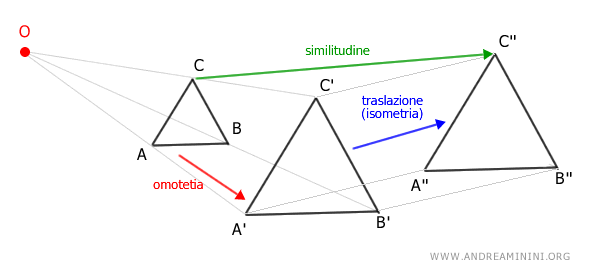
• La composizione di due similitudini è ancora una similitudine
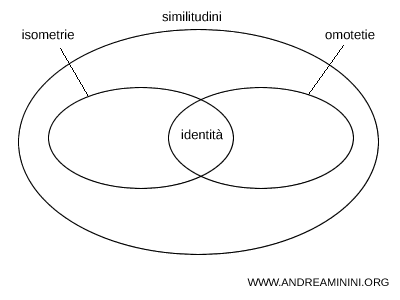
  La composizione di due similitudini con rapporto di scala k₁ e k₂ è uguale a una similitudine con rapporto k₁·k₂.
• Le isometrie e le omotetie sono casi particolari di similitudini
  Le isometrie e le omotetie appartengono al gruppo più generale delle similitudini, che comprende tutte le trasformazioni del piano che conservano angoli e rapporti di lunghezza.
  • Le isometrie sono similitudini con rapporto unitario $ k=1 $, cioè conservano le distanze.
  • Le omotetie sono le similitudini con centro fisso e senza rotazione o traslazione, cioè agiscono moltiplicando tutte le distanze da un punto per un certo fattore $ k $.
  Pertanto, tutte le isometrie e le omotetie sono similitudini. Tuttavia, non tutte le similitudini sono isometrie e/o omotetie. Infatti:
  • Non tutte le similitudini sono isometrie, perché nelle similitudini il rapporto di scala può essere diverso da 1 ( $ k \ne 1 $ ), mentre nelle isometrie deve essere $ k=1 $.
  • Non tutte le similitudini sono omotetie, perché una similitudine può includere anche rotazioni, traslazioni o simmetrie, oltre alla dilatazione.
  Quindi, le isometrie e le omotetie sono sottoinsiemi dell'insieme delle similitudini. Le similitudini costituiscono quindi un insieme più ampio, che contiene come casi particolari sia le isometrie quando $ k = 1 $, sia le omotetie quando non c’è rotazione o traslazione.
  
• Due figure congruenti sono anche figure simili
  Due figure geometriche congruenti sono anche figure simili, perché la congruenza posso vederla come la composizione di una omotetia con centro qualsiasi e un rapporto di proporzionalità uguale 1 seguita o preceduta da una isometria qualsiasi (identità, traslazione, rotazione, simmetria centrale o assiale).
• Centro della similitudine
  Nel piano una similitudine che non sia una traslazione ha sempre un punto fisso, ovvero un invariante della trasformazione che corrisponde a se stesso detto "centro della similitudine".
• Similitudini dirette e indirette
  Nel piano una similitudine è diretta se conserva lo stesso orientamento rispetto al piano. Viceversa, se non lo mantiene, è una similitudine indiretta.
• Il rapporto tra i perimetri di due figure simili
  Nel piano, se due figure sono simili con rapporto di similitudine $ k $, allora il rapporto tra i loro perimetri è pari al rapporto di similitudine stesso, cioè $ k $. In particolare, se $ F' $ è l'immagine della figura $ F $ tramite una similitudine di rapporto $ k $, vale la seguente relazione: $$ Perimetro(F') = k \cdot Perimetro(F) $$

  Nota. Una similitudine moltiplica ogni lunghezza per $ k $. Poiché il perimetro è una misura lineare (somma dei lati), esso viene moltiplicato per $ k $. Ad esempio, se il perimetro di un quadrato è $ P = 4L $, allora il perimetro di un quadrato simile, con lato $ kL $, risulta $$ P' = 4(kL) = k \cdot (4L) = k \cdot P $$

• Il rapporto tra le aree di due figure simili
  Nel piano due figure simili con un rapporto di similitudine $ k $, hanno il rapporto tra le loro aree pari al quadrato del rapporto di similitudine ovvero k². In particolare, se $ F' $ è l'immagine della figura $ F $ tramite una similitudine di rapporto $ k $, vale la seguente relazione: $$ Area(F') = k^2 \cdot Area(F) $$

  Nota. Questa proprietà deriva dal fatto che una similitudine moltiplica tutte le lunghezze per $ k $. Poiché l’area dipende da due dimensioni lineari, il fattore di scala diventa $ k \cdot k = k^2 $. Ad esempio, se l’area di un quadrato è $ A = L \cdot L $, allora l’area di un quadrato simile, con lato $ kL $, risulta $$ A' = (kL) \cdot (kL) = k^2 \cdot (L \cdot L) $$

• l rapporto tra i volumi di due solidi simili
  Nello spazio a tre dimensioni, se due solidi sono simili con rapporto di similitudine \(k\), allora il rapporto tra i loro volumi è pari al cubo del rapporto stesso, cioè \(k^3\). In particolare, se \(F'\) è l’immagine del solido \(F\) tramite una similitudine di rapporto \(k\), vale la relazione: \[ \text{Volume}(F') = k^3 \cdot \text{Volume}(F) \]

  Nota. Una similitudine moltiplica ogni lunghezza per \(k\). Poiché il volume si ottiene moltiplicando tre dimensioni lineari, il fattore di scala diventa \(k^3\). Ad esempio, se un cubo ha lato \(L\), il suo volume è \(V = L \cdot L \cdot L\). Un cubo simile, con lato \(kL\), avrà volume: \[ V' = (kL)\cdot(kL)\cdot(kL) = k^3 \cdot (L \cdot L \cdot L) = k^3 \cdot V \]

E così via.