Il secondo teorema di Euclide
In un triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa ha la stessa area del rettangolo con i lati congruenti alla proiezione dei cateti sull'ipotenusa.
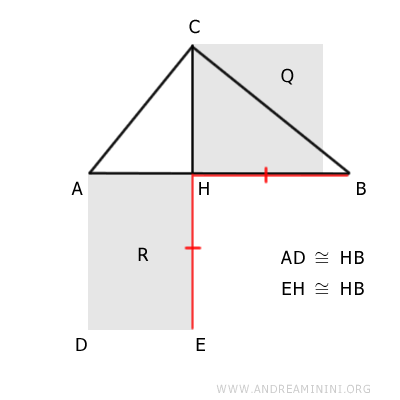
In altre parole, considero un quadrato Q che ha per lato l'altezza CH del triangolo rettangolo rispetto all'ipotenusa AB.
La proiezione dei cateti sull'ipotenusa la divide in due segmenti AH e BH. Quindi, costruisco un rettangolo R con questi due segmenti.
Il quadrato Q e il rettangolo R sono poligoni equivalenti, ossia hanno la stessa area.
Corollario
Come corollario si può dire che in un triangolo rettangolo l'altezza relativa all'ipotenusa è il medio proporzionale tra le proiezioni dei cateti sull'ipotenusa.
Pertanto, in una proporzione una proiezione (p1) sta all'altezza (h) come l'altezza sta all'altra proiezione (p2) del cateto sull'ipotenusa.
Nota. La proporzione p1:h=h:p2 è equivalente al secondo teorema di Euclide $$ p_1 : h = h : p_2 \rightarrow h^2 = p_1 \cdot p_2 $$ ovvero l'area del quadrato costruito sull'altezza è uguale all'area del rettangolo costruito con le proiezioni dei cateti sull'ipotenusa.
Teorema inverso
Se in un triangolo il quadrato dell'altezza è uguale al prodotto delle lunghezze dei due segmenti in cui il lato opposto è diviso dall'altezza, allora il triangolo è rettangolo. $$ \overline{CH}^2 = \overline{AH} \cdot \overline{BH} $$
In questo caso il vertice (C) da cui ha origine l'altezza è un angolo retto (90°).
Un esempio
Prendo come esempio questo triangolo rettangolo ABC
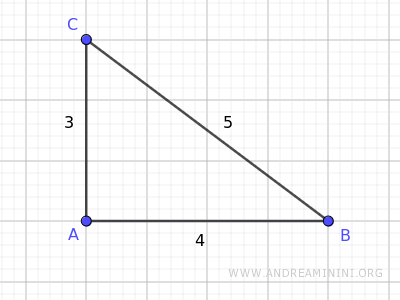
Il triangolo rettangolo ha come cateti AB=4 e AC=3 e come ipotenusa BC=5
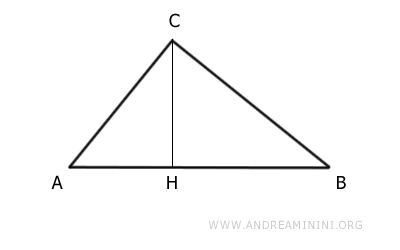
Traccio l'altezza del triangolo rispetto all'ipotenusa.
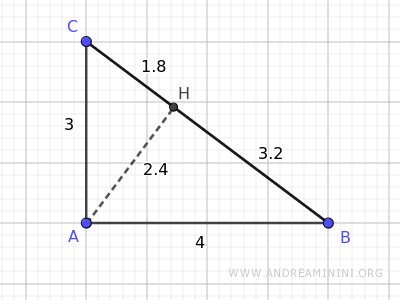
L'altezza AH del triangolo misura 2.4 e divide l'ipotenusa in due segmenti di lunghezza 1.8 e 3.2
Il quadrato dell'altezza ha un'area pari a 5.76
$$ \overline{AH}^2 = 2.4^2 = 5.76 $$
L'area di un rettagolo che ha un lato lungo 1.8 e l'altro lato lungo 3.2 è sempre 5.76
$$ \overline{BH} \cdot \overline{CH} = 3.2 \cdot 1.8 = 5.76 $$
Pertanto il quadrato e il rettangolo hanno la stessa area, ovvero sono poligoni equivalenti.
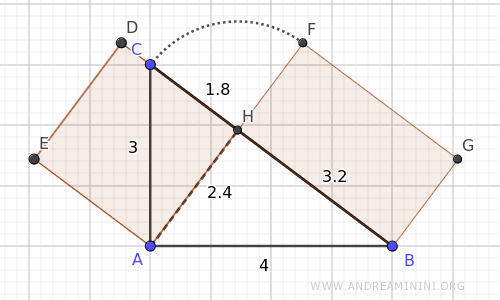
La dimostrazione
Considero un triangolo rettangolo ABC.
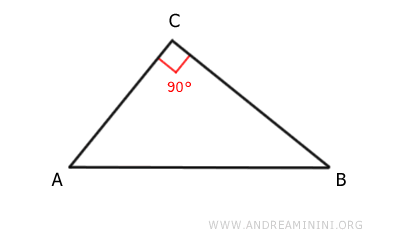
I cateti del triangolo rettangolo sono i segmenti AC e BC.
Il segmento CH è, invece, l'altezza del triangolo relativa all'ipotenusa AB.
Costruisco un quadrato Q1 sull'altezza CH.
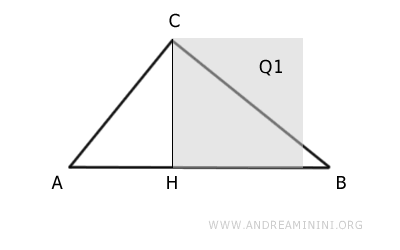
Il punto H è anche la proiezione dei cateti che divide l'ipotenusa in due segmenti AH e BH
$$ \overline{AB} = \overline{AH} + \overline{BH} $$
Costruisco un rettangolo R1 sul segmento AH che ha i lati laterali congruenti AD≅EH≅AB con l'ipotenusa AB.
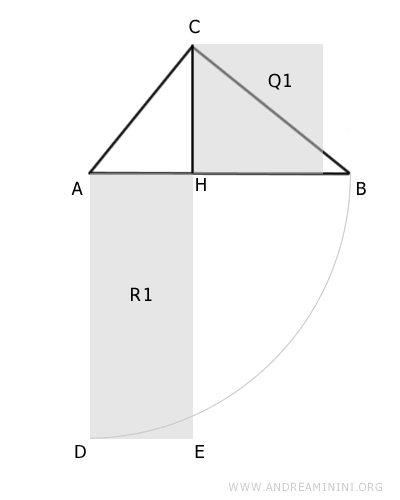
Posso considerare il rettangolo R1 come un poligono composto da un quadrato Q2 con lato congruente ad AH e un rettangolo R2.
$$ R1 \doteq Q2 + R2 $$
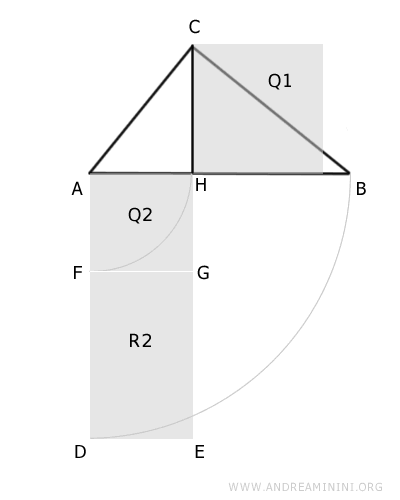
E' importante notare che il rettangolo R2 ha per lati le proiezioni dei cateti del triangolo ABC sull'ipotenusa ovvero AH≅FG≅DE e BH≅FD≅EG.
$$ AH \cong FG \cong DE $$
$$ BH \cong FD \cong EG $$
Quindi, devo dimostrare che il quadrato Q1 e il rettangolo R2 sono poligoni equivalenti, ovvero con la stessa area.
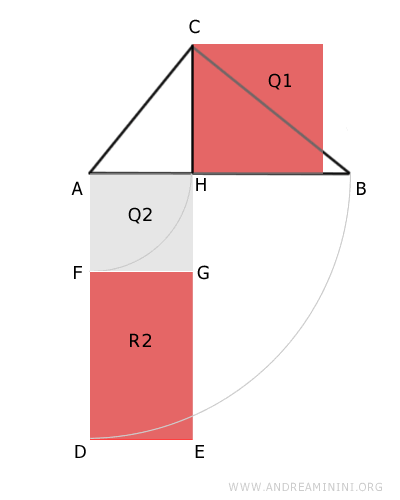
Ora focalizzo l'attenzione sul triangolo rettangolo AHC ossia su una componente all'interno del triangolo ABC.
In base al teorema di Pitagora la somma dei quadrati costruiti sui cateti del triangolo AHC è uguale al quadrato sull'ipotenusa AC.
$$ Q3 \doteq Q1 + Q2 $$
Da questo deduco che la superficie del quadrato Q1 è uguale alla differenza tra Q3 e Q2.
$$ Q1 \doteq Q3 - Q2 $$
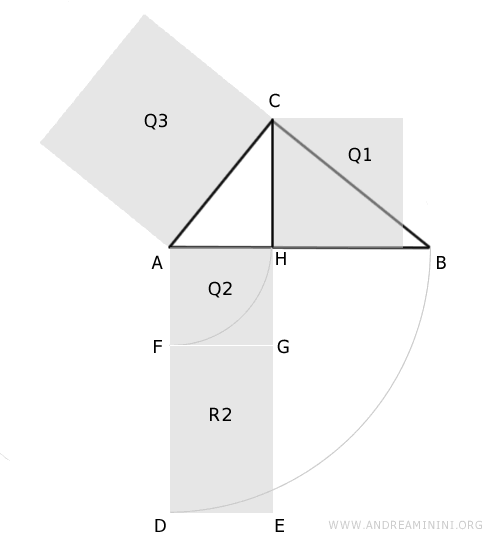
In base al primo teorema di Euclide l'area Q3 è uguale all'area R1=Q2+R2
$$ Q3 \doteq R1 $$
$$ Q3 \doteq Q2 + R2 $$
Quindi anche R2 è equivalente a Q3-Q2
$$ R2 \doteq Q3 - Q2 $$
Di conseguenza sia Q1 che R2 sono equivalenti a Q3-Q2.
$$ R2 \doteq Q3 - Q2 \dot Q1 $$
Pertanto, per la proprietà transitiva Q1 e R2 sono equivalenti ossia hanno la stessa area.
$$ R2 \doteq Q1 $$
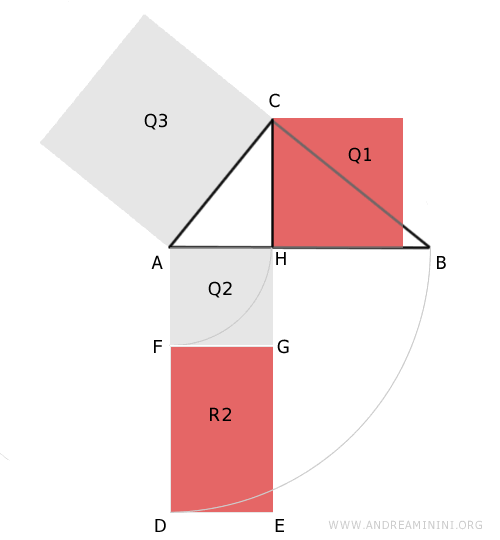
Questo dimostra che il quadrato Q1 costruito sull'altezza CH relativa all'ipotenusa AB del triangolo ABC è equivalente al rettangolo R2 che ha per lati le proiezioni AH≅FG e BH≅DF dei cateti
Corollario
In un triangolo rettangolo l'altezza (h) relativa all'ipotenusa è il medio proporzionale tra le proiezioni p1 e p2 dei cateti sull'ipotenusa.
$$ p_1 : h = h : p_2 $$
In altre parole, la proiezione del cateto minore (p1) sta all'altezza (h) come l'altezza sta alla proiezione del cateo maggiore (p2).
Questo vuole dire che il quadrato costruito sull'altezza è equivalente, ovvero ha la stessa area, del rettangolo costruito su una proiezione che ha per altezza l'altra proiezione.
$$ \frac{p_1}{h} = \frac{h}{p_2} $$
$$ h^2 = p_1 \cdot p_2 $$
Si ritorna così al secondo teorema di Euclide.

Esempio
Per fare un esempio considero il triangolo rettangolo ABC di cui conosco tutte le misure.

In questo caso la lunghezza del cateto minore (AC) è uguale a 3, quella del cateto maggiore (AB) è 4.
Infine, l'altezza relativa all'ipotenusa misura 2.4
Secondo il corollario del secondo teorema di Euclide deve valere la seguente proporzione
$$ p_1 : h = h : p_2 $$
So già che l'altezza (h) relativa all'ipotenusa misura 2.4
$$ p_1 : 2.4 = 2.4 : p_2 $$
In questo esempio la proiezione del cateto minore (p1) sull'ipotenusa ha una lunghezza pari a 1.8, mentre la proiezione del cateto maggio (p2) è 3.2
$$ 1.8 : 2.4 = 2.4 : 3.2 $$
Trasformo la proporzione in una frazione equivalente e svolgo i calcoli
$$ \frac{1.8}{2.4} = \frac{2.4}{3.2} $$
$$ 0.75 = 0.75 $$
La proporzione è soddisfatta.
La dimostrazione
Considero un triangolo rettangolo ABC.
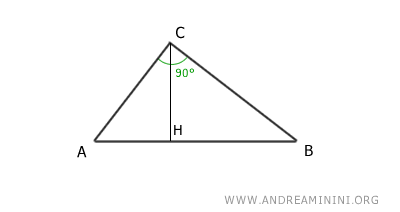
L'altezza relativa all'ipotenusa (CH) divide l'angolo retto in due angoli complementari γ1 e γ2 la cui somma è pari a γ1+γ2=90°.
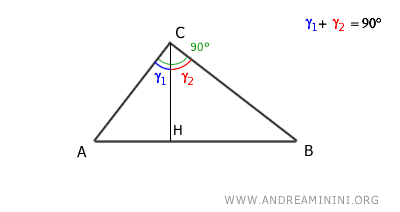
L'altezza divide CH divide il triangolo in due triangoli rettangoli ACH e CBH.
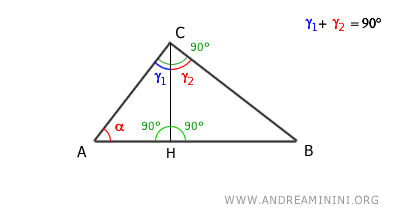
Sapendo che la somma degli angoli interni di un triangolo è sempre uguale a un angolo piatto (180°)
$$ \alpha + \gamma_1 + 90° = 180° $$
deduco che nel triangolo ACH gli angoli α e γ1 sono angoli complementari.
$$ \alpha + \gamma_1 = 180° - 90° $$
$$ \alpha + \gamma_1 = 90° $$
Poiché α+γ1=90° e γ1+γ2=90° deduco che gli angoli α e γ2 sono angoli congruenti α≅γ2 perché sono complementari dello stesso angolo.
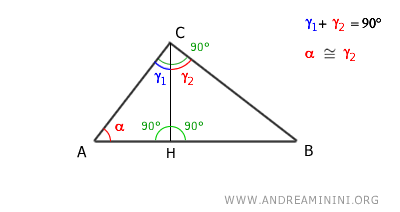
Per il primo criterio di similitudine dei triangoli, i due triangoli ACH e CBH sono simili perché hanno due angoli congruenti: l'angolo retto (90°) e gli angoli acuti congruenti α≅γ2
$$ ACH \approx CBH $$
Essendo due triangoli simili, i triangoli ACH e CBH hanno i lati omologhi proporzionali.
$$ \overline{AC} : \overline{BC} = \overline{AH} : \overline{CH} = \overline{CH} : \overline{BH} $$
Questo dimostra il corollario del secondo teorema di Euclide.
$$ \overline{AH} : \overline{CH} = \overline{CH} : \overline{BH} $$
Dove AH è la proiezione p1 sull'ipotenusa del cateto minore, mentre BH è la proiezione p2 del cateto maggiore sull'ipotenusa.
$$ p_1 : \overline{CH} = \overline{CH} : p_2 $$
Infine, CH è l'altezza del triangolo rettangolo ABC relativa all'ipotenusa.
$$ p_1 : h = h : p_2 $$
E così via.
