Il teorema del lato e angolo maggiore dei triangoli

In ogni triangolo non equilatero il lato di lunghezza maggiore è il lato opposto all'angolo di ampiezza maggiore. E viceversa.

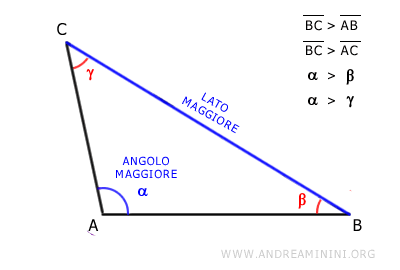
Questo teorema vale per tutti i triangoli, ad eccezione del triangolo equilatero.

Non vale per il triangolo equilatero, perché quest'ultimo ha tre lati e tre angoli congruenti, quindi non c'è un lato maggiore e un angolo maggiore.

Un esempio pratico

Prendo come esempio un triangolo scaleno e ottusangolo.

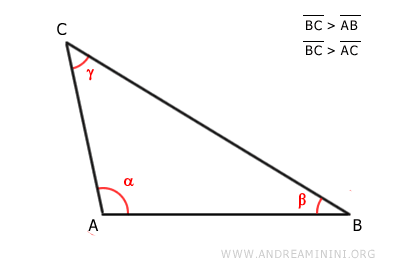
L'angolo maggiore è l'angolo alfa in corrispondenza del vertice A.

$$ \alpha > \beta $$

$$ \alpha > \gamma $$

Il lato opposto all'angolo maggiore alfa è il lato AB che è anche il lato maggiore del triangolo.

$$ \overline{BC} > \overline{AB} $$

$$ \overline{BC} > \overline{AC} $$

E ovviamente vale anche l'inverso.

La dimostrazione

Per ipotesi iniziale, considero il triangolo ABC in cui il lato BC è maggiore degli altri due lati.

$$ \overline{BC} > \overline{AC} $$

$$ \overline{BC} > \overline{AB} $$

Devo dimostrare che l'angolo opposto al lato maggiore BC, ossia l'angolo α, è maggiore degli altri due angoli.

Punto il compasso sul vertice C e con raggio CA traccio un arco che interseca il lato CB.

Chiamo questo punto D.

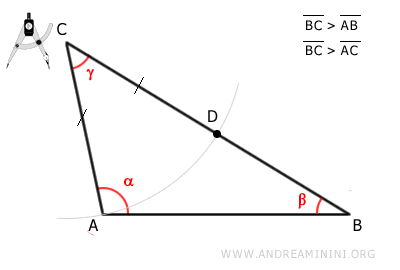
Pertanto, il segmento CD è congruente con il segmento AC.

$$ \overline{CD} \cong \overline{AC} $$

Traccio un segmento AD.

I punti ACD formano un triangolo isoscele, in quanto i lati AC e CD sono congruenti.

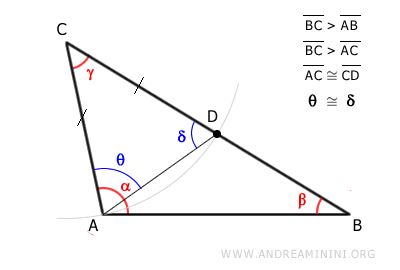
Essendo un triangolo isoscele, il triangolo ACD ha due angoli congruenti δ e θ adiacenti alla base AD.

$$ δ \cong θ $$

L'angolo δ è un angolo esterno del triangolo ABD.

Quindi, in base al teorema dell'angolo esterno dei triangoli, l'angolo esterno δ è maggiore rispetto agli altri due angoli interni non adiacenti come β e α-θ del triangolo ABD

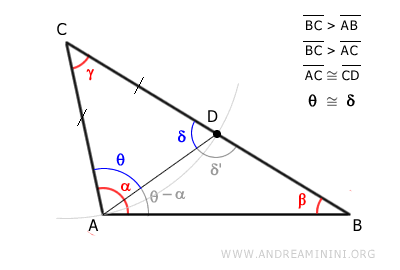
In particolar modo mi interessa sapere che l'angolo δ è maggiore di β

$$ \delta > \beta $$

Sapendo che gli angoli δ e θ sono congruenti (δ≅θ) anche l'angolo θ è maggiore di β

$$ θ > \beta $$

A sua volta l'angolo θ ha un'ampiezza minore dell'angolo α, ossia θ<α, perché ha un lato coincidente e l'altro lato interno all'angolo α

Pertanto, l'angolo α è maggiore dell'angolo β

$$ \alpha > \beta $$

A questo punto devo dimostrare che l'angolo α sia anche maggiore dell'angolo γ

Riprendo il triangolo iniziale ABC, punto il compasso sul punto B e traccio un arco di raggio AB fino a intersecare il lato AC.

In questo modo individuo il punto E.

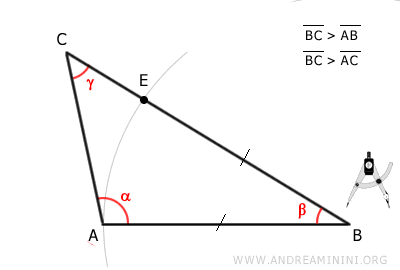
Di conseguenza, il segmento EB è congruente con il segmento AB.

$$ \overline{EB} \cong \overline{AB} $$

Traccio un segmento AE.

I punti ABE formano un triangolo isoscele poiché i lati AB e EB sono congruenti.

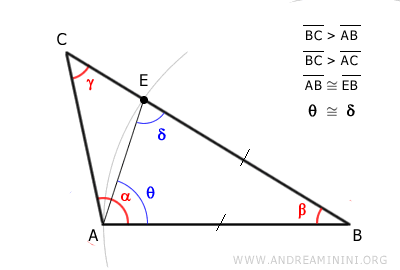
Essendo un triangolo isoscele, anche il triangolo ABE ha due angoli congruenti δ e θ adiacenti alla base AE.

$$ δ \cong θ $$

A sua volta, l'angolo δ è un angolo esterno del triangolo ACE.

In base al teorema dell'angolo esterno dei triangoli, l'angolo esterno δ è maggiore rispetto agli altri due angoli interni non adiacenti come γ e α-θ del triangolo ACE

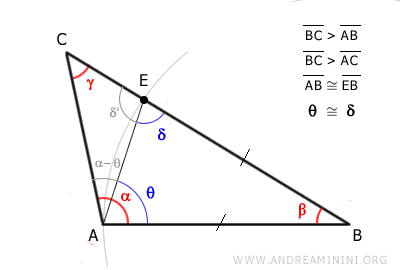
In particolar modo, mi è utile sapere l'angolo δ è maggiore di γ

$$ \delta > \gamma $$

Poiché gli angoli δ e θ sono congruenti (δ≅θ) anche l'angolo θ è maggiore di γ

$$ θ > \gamma $$

A sua volta l'angolo θ ha un'ampiezza inferiore rispetto all'angolo α ossia θ < α.

Pertanto, l'angolo α è maggiore dell'angolo γ

$$ \alpha > \beta $$

In conclusione, l'angolo α opposto al lato maggiore BC è maggiore sia rispetto all'angolo β che all'angolo γ

Quindi, l'angolo α è il lato maggiore del triangolo ABC.

Osservazioni

Alcune osservazioni e corollari del teorema:

• In un triangolo rettangolo l'ipotenusa è sempre il lato maggiore di ciascun cateto.
• In un triangolo ottusangolo il lato opposto all'angolo ottuso è sempre il lato maggiore rispetto agli altri due lati.
• Corollario
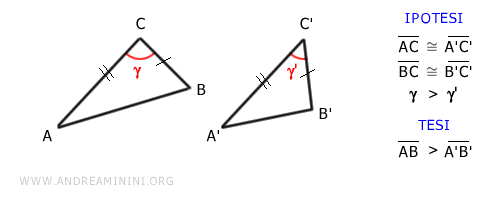
  Se due triangoli hanno due lati congruenti nello stesso ordine (es. AC≅A'C' e BC≅B'C') ma l'angolo compreso diverso, quello con l'angolo di ampiezza maggiore (es. γ>γ') ha anche il terzo lato maggiore (es. AB>A'B').
  

E così via.