Angoli complementari

Una coppia di angoli sono detti angoli complementari se la loro somma è uguale a 90° gradi ossia π/2 radianti.

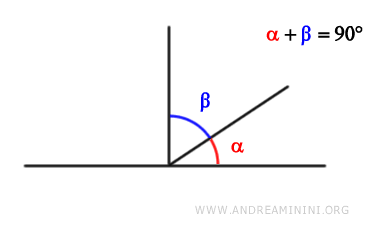
Il termine "complementare" deriva dal latino "complementum" e significa "ciò che completa".

In questo caso, un angolo completa l'altro formando un angolo retto, che è di 90 gradi.

Nota. Non importa quale sia l'ampiezza dei due angoli, ciò che conta è che la loro somma sia uguale a 90°.

Un esempio pratico

Ad esempio, considero due angoli alfa e beta

$$ \alpha = 30° $$

$$ \beta = 60° $$

Sono angoli complementari perché la loro somma è uguale a 90°

$$ \alpha + \beta = 30° + 60° = 90° $$

Dal punto di vista grafico

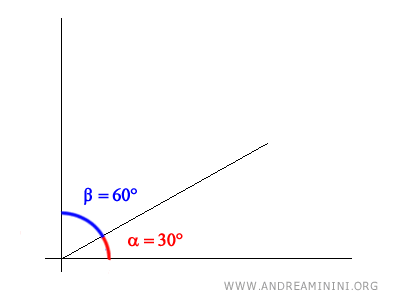
Ogni angolo ha un suo angolo complementare.

Ad esempio, considero l'angolo

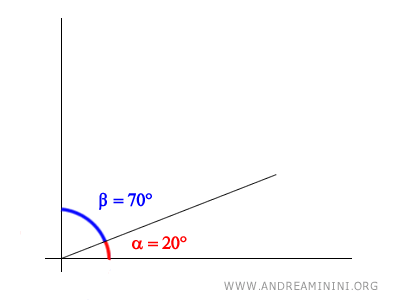
$$ \alpha = 20° $$

Per trovare l'angolo complementare basta calcolare la differenza rispetto all'angolo retto (90°).

$$ \beta = 90° - \alpha $$

$$ \beta = 90° - 20° $$

$$ \beta = 70° $$

In questo caso l'angolo complementare ha un'ampiezza di 70°.

Osservazioni

Alcune proprietà e osservazioni sugli angoli complementari

• Se due angoli a e b sono complementari allo stesso angolo c, allora i due angoli a e b sono congruenti. $$ \alpha + \gamma = 90° \ , \ \beta + \gamma = 90° \ \Longrightarrow \ \alpha \cong \beta $$

  Dimostrazione. Questo è dovuto al fatto che la somma degli angoli è costante (90 gradi), quindi se un angolo è fisso, l'altro deve necessariamente essere lo stesso per entrambi gli angoli. Sapendo che $$ \alpha + \gamma = 90° $$ $$ \beta + \gamma = 90° $$ Ricavo l'angolo gamma per differenza tra l'angolo retto e l'angolo beta. $$ \gamma = 90° - \beta $$ Poi sostituisco γ=90-β nell'equazione α+γ=90 $$ \alpha + \gamma = 90° $$ $$ \alpha + ( 90° - \beta ) = 90° $$ $$ \require{cancel} \alpha + \cancel{90°} - \beta = \cancel{90°} $$ $$ \alpha - \beta = 0° $$ La differenza tra gli angoli alfa e beta è nulla e questo vuol dire che hanno la stessa ampiezza. Quindi, gli angoli alfa e beta sono congruenti. $$ \alpha \cong \beta $$

• Se un angolo è complementare a un secondo angolo, e quest'ultimo è complementare a un terzo angolo, allora il primo e il terzo angolo sono uguali. $$ \alpha + \beta = 90° \ , \ \beta + \gamma = 90° \ \Longrightarrow \ \alpha \cong \gamma $$

  Dimostrazione. Sapendo che $$ \alpha + \beta = 90° $$ $$ \beta + \gamma = 90° $$ Ricavo l'angolo beta per differenza tra l'angolo retto e l'angolo gamma. $$ \beta = 90° - \gamma $$ Poi sostituisco β=90-γ nell'equazione α+β=90 $$ \alpha + \beta = 90° $$ $$ \alpha + ( 90° - \gamma ) = 90° $$ $$ \require{cancel} \alpha + \cancel{90°} - \gamma = \cancel{90°} $$ $$ \alpha - \gamma = 0° $$ Se la differenza tra gli angoli alfa e gamma è nulla, gli angoli hanno la stessa ampiezza. Quindi, sono angoli congruenti. $$ \alpha \cong \gamma $$

• Se due angoli α e β sono complementari a uno stesso angolo γ, allora i due angoli α e β sono congruenti, ossia hanno la stessa ampiezza.

  Dimostrazione. Considero due coppie di angoli complementari $$ \alpha + \gamma = 90° $$ $$ \beta + \gamma = 90° $$ Ricavo gli angoli alfa e beta per differenza rispetto all'angolo retto $$ \alpha = 90° - \gamma $$ $$ \beta = 90° - \gamma $$ Questo dimostra che i due angoli α e β hanno la stessa ampiezza. $$ \alpha = \beta = 90° - \gamma $$ Quindi, gli angoli α e β sono angoli congruenti

• Il seno di un angolo è uguale al coseno del suo angolo complementare. $$ \alpha + \beta = 90° \Longrightarrow \sin( \alpha) = \cos( \beta) $$

  Ad esempio, gli angoli 70° e 20° sono complementari perché la loro somma è un angolo retto $$ 70° + 20° = 90° $$ Il coseno di 70° è uguale al seno di 20° $$ \cos(70°) = \sin(20°) = 0,94 $$ Questo accade perché in trigonometria, la relazione tra angoli complementari è fondamentale. Le funzioni trigonometriche di angoli complementari sono strettamente correlate tra loro.
  
  Dimostrazione. Considero la circonferenza goniometrica e un angolo alfa (α) che genera un triangolo rettangolo OAB.
  
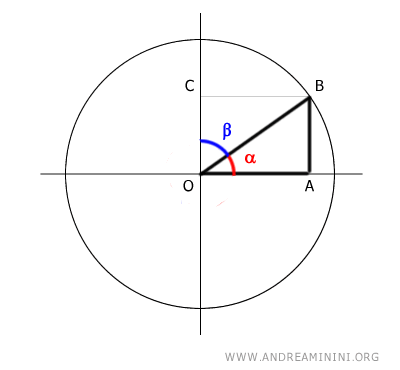
  Il seno dell'angolo alfa (α) è il rapporto tra il cateto opposto (AB) all'angolo α e l'ipotenusa (OB). $$ \sin \alpha = \frac{ \overline{AB} }{ \overline{OB} } $$ Il coseno dell'angolo alfa (α) è il rapporto tra il cateto adicente (OA) all'angolo α e l'ipotenusa (OB). $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } $$ L'angolo complementare all'angolo α è l'angolo β. $$ \alpha + \beta = 90° $$ Sapendo che i segmenti OA e CB sono congruenti $$ \overline{OA} \cong \overline{CB} $$ posso ottenere il coseno anche dal rapporto CB/OB $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } = \frac{ \overline{CB} }{ \overline{OB} } $$ Se considero il triangolo OBC, quello di colore viola, il segmento CB è il cateto opposto all'angolo β.
  
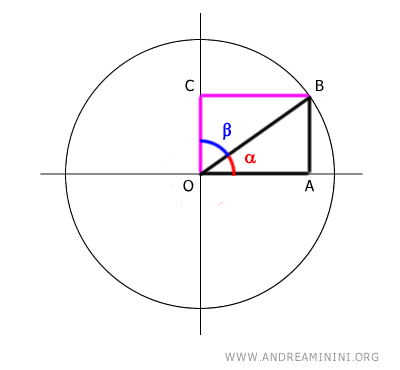
  Quindi il rapporto CB/OB è il seno dell'angolo beta. $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } = \frac{ \overline{CB} }{ \overline{OB} } = \sin \beta $$ Ne consegue che il coseno dell'angolo alfa è uguale al seno dell'angolo complementare beta $$ \cos \alpha = \sin \beta $$ Inoltre, sapendo che anche i segmenti AB e OC sono congruenti, ossia hanno la stessa lunghezza $$ \overline{AB} = \overline{OC} $$ Seguendo un ragionamento simile $$ \sin \alpha = \frac{ \overline{AB} }{ \overline{OB} } = \frac{ \overline{OC} }{ \overline{OB} } = \cos \beta $$ giungo alla conclusione che il seno dell'angolo alfa è uguale al coseno dell'angolo complementare beta $$ \sin \alpha = \cos \beta $$ E' ciò che volevo dimostrare.

Gli angoli complementari sono un concetto chiave nella geometria e hanno molte applicazioni pratiche.

Ad esempio, sono usati nella progettazione e costruzione di edifici e strutture, poiché molte strutture utilizzano angoli retti. Sono utilizzati nella navigazione, nella cartografia e in molte altre discipline scientifiche.

E così via.