La funzione trigonometrica seno
Nella circonferenza goniometrica la funzione trigonometrica seno associa l'ampiezza di un angolo α a un segmento sull'asse verticale. Si indica con sin(α) o sen(α) nei testi italiani e può assumere un valore compreso tra -1 e +1.
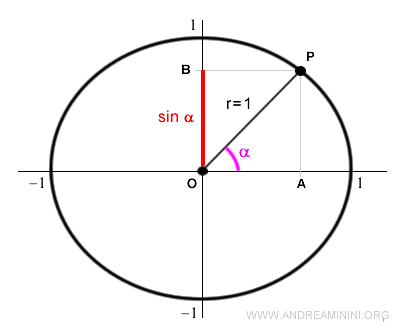
L'angolo α individua un punto P sulla circonferenza goniometrica.
La proiezione del punto P sull'asse verticale determina la lunghezza del segmento OB detto seno di α.
Nota. Il seno può essere misurato in modo equivalente sia con il segmento OB che con il segmento AP $$ \overline{OB} = \overline{AP} $$
In generale, il seno di un angolo α è il rapporto tra il cateto opposto all'angolo e l'ipotenusa di un triangolo rettangolo.
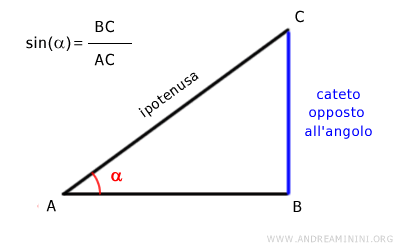
La lunghezza massima del segmento è uguale al raggio della circonferenza goniometrica.
Poiché la circonferenza goniometrica ha raggio unitario (r=1) ne consegue che la funzione seno assume valori compresi tra 1 e -1.
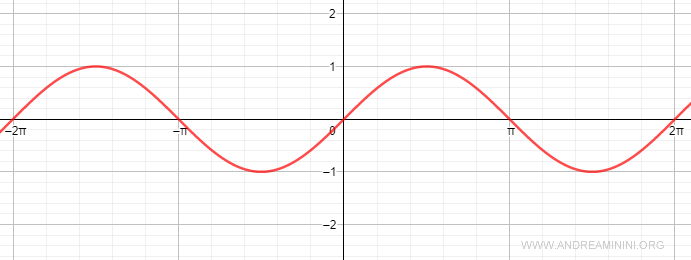
Pertanto, il dominio della funzione seno è l'insieme dei numeri reali $ \mathbb{R} $ mentre il codominio è l'intervallo [-1;1].
$$ -1 \le \sin \alpha \le 1 $$
La funzione seno è crescente in \( \left[-\frac{\pi}{2} , \frac{\pi}{2}\right] \) ed è decrescente in \( \left[\frac{\pi}{2} , \frac{3\pi}{2}\right] \).
Ecco alcuni angoli importanti della funzione seno
| angolo (gradi) | angolo (radianti) | seno |
|---|---|---|
| $$ 0° $$ | $$ 0 $$ | $$ 0 $$ |
| $$ 30° $$ | $$ \frac{\pi}{6} $$ | $$ \frac{1}{2} $$ |
| $$ 45° $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ |
| $$ 60° $$ | $$ \frac{\pi}{3} $$ | $$ \frac{\sqrt{3}}{2} $$ |
| $$ 90° $$ | $$ \frac{\pi}{2} $$ | $$ 1 $$ |
| $$ 180° $$ | $$ \pi $$ | $$ 0 $$ |
| $$ 270° $$ | $$ \frac{3 \pi}{2} $$ | $$ -1 $$ |
Il seno è una funzione periodica di periodo 2π.
Dove 2π indica un giro completo della circonferenza goniometrica ossia un angolo giro (360°).
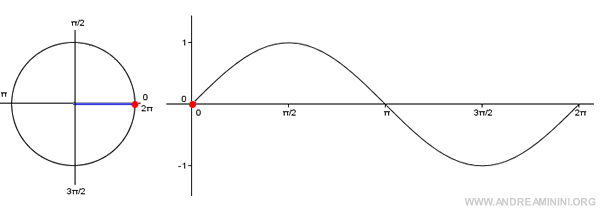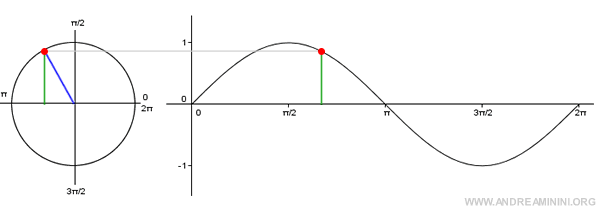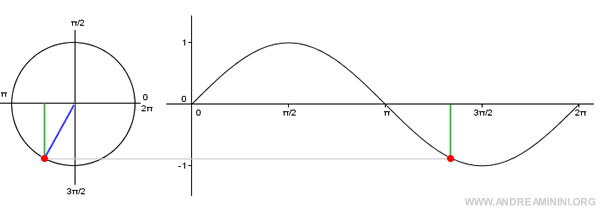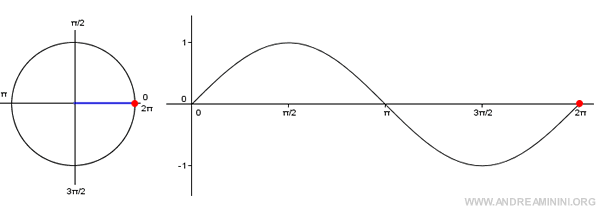
Nota. Il grafico della funzione seno è detto sinusoide. Si costruisce indicando sull'asse x i valori degli angoli e sull'asse y le ordinate della circonferenza goniometrica. Poiché il seno è una funzione periodica, è sufficiente indicare gli angoli nell'intervallo [0;2π].
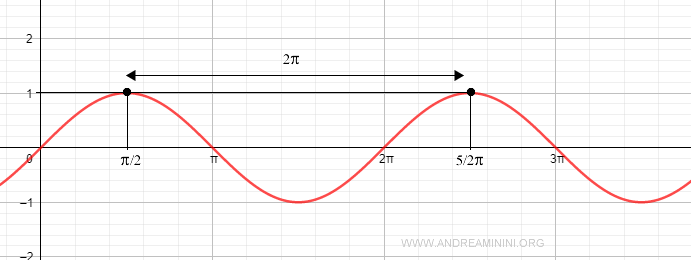
Se a un determinato angolo α aggiungo uno o più angoli giri (2π), individuo lo stesso il punto P sulla circonferenza goniometrica e la funzione seno restituisce sempre lo stesso valore.
$$ \sin \alpha = \sin ( \alpha + n \cdot 2 \pi ) \ \ \ \text{con} \ \ n \in \mathbb{Z} $$
Ad esempio, le funzioni sin(π/2) e sin(π/2+2π) restituiscono il valore uno.
Nota. Da un punto di vista matematico la funzione seno è anche una funzione dispari perché $$ \sin(- \alpha) = - \sin \alpha $$ Le funzione seno di un angolo orientato (α) e del suo opposto (-α) hanno lo stesso valore ma segno diverso.
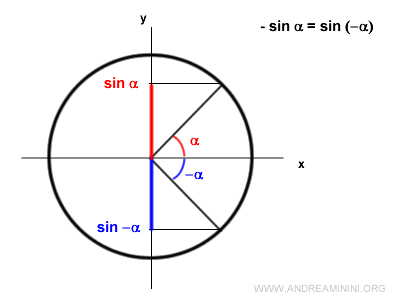
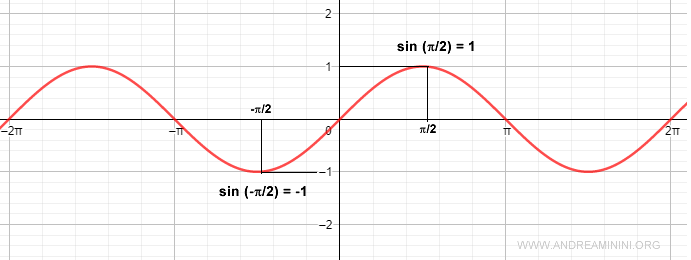
Ad esempio, il seno di π/2 è +1 mentre il seno di -π/2 è -1.
L'origine della parola seno
La parola seno deriva dal termine indiano "jiiva" usato dal matematico e astronomo Aryabhata nel V secolo d.C. per indicare le mezze corde di una circonferenza.
Il termine "jiiva" fu successivamente tradotto dagli arabi in "jaib" che vuol dire "piega".
Successivamente, in Europa venne tradotto il termine "piega" dall'arabo jaib al latino "sinus".
E così via.
