Il primo criterio di congruenza dei triangoli

Il primo principio di congruenza dei triangoli afferma che due triangoli sono congruenti se hanno congruenti nello stesso ordine due lati e l'angolo compreso tra di essi.

In altre parole, presi due lati nello stesso ordine, due triangoli sono congruenti se i lati hanno la stessa lunghezza e l'angolo compreso tra questi ha la stessa ampiezza in entrambi i triangoli.

Questo criterio di congruenza è anche noto come criterio LAL (Lato-Angolo-Lato)

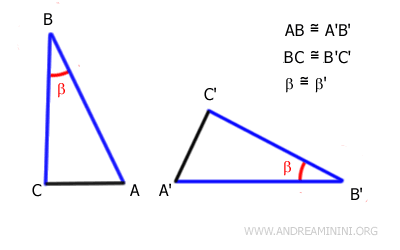
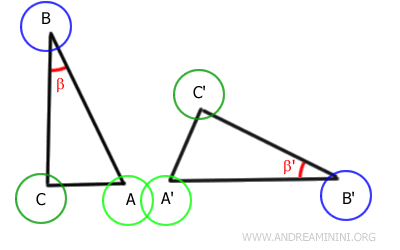
Ad esempio, considero questi due triangoli ABC e A'B'C'

I lati AB e BC del primo triangolo sono rispettivamente congruenti ai lati A'B' e B'C' del secondo triangolo, ossia hanno la stessa lunghezza pur essendo disposti in modo diverso.

$$ \overline{AB} \cong \overline{A'B'} $$

$$ \overline{BC} \cong \overline{B'C'} $$

Anche gli angoli β e β' compresi tra le due coppie di lati sono congruenti, ossia hanno la stessa ampiezza.

$$ \beta \cong \beta ' $$

Pertanto, in base al primo principio di congruenza, i due triangoli sono congruenti.

Se l'angolo congruente non è compreso tra i due lati, non è detto che il triangolo sia congruente. Ad esempio, considero il triangolo ABC. Poi disegno un cerchio di raggio AC e centro A. L'arco interseca il prolungamento del segmento AC nel punto D. In questo modo posso disegnare un altro triangolo ACD con due lati congruenti rispetto al precedente.

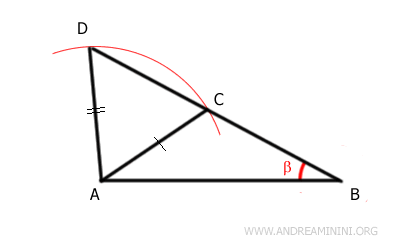
E' evidentre che i due triangoli ABC e ABD non sono congruenti, perché non sono sovrapponibili. Il triangolo ABD è più grande del triangolo ABC. Tuttavia, entrambi i triangoli hanno due lati congruenti AB≅AB e AC≅AD e l'angolo β congruente. Tuttavia, l'angolo β non è compreso tra i due lati congruenti. In conclusione, due lati congruenti e un angolo non compreso tra di essi non sono sufficienti a dichiarare la congruenza dei triangoli.

La dimostrazione

Il primo criterio di congruenza è da considerarsi un postulato perché si basa sugli assiomi di Euclide.

Pertanto, quella che segue non è una vera dimostrazione, in quanto i movimenti rigidi sono solo dei concetti intuitivi.

Considero due triangoli ABC e A'B'C'

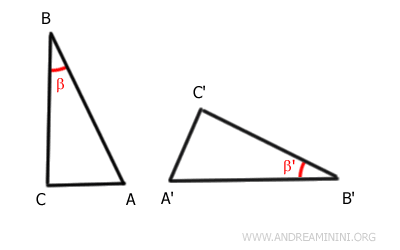
Per ipotesi iniziale, sono sovrapponibili i segmenti AB e A'B', i segmenti BC e B'C' e gli angoli tra di essi β e β'.

Con un movimento rigido (rotazione+traslazione) sovrappongo il lato AB sul lato A'B', facendo in modo che si sovrapponga anche l'angolo β sull'angolo β'.

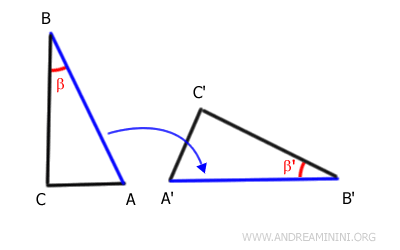
Essendo AB e A'B' dei lati sovrapponibili, anche i loro estremi si sovrappongono.

Pertanto, il punto A si sovrappone al punto A' e il punto B si sovrappone al punto B'

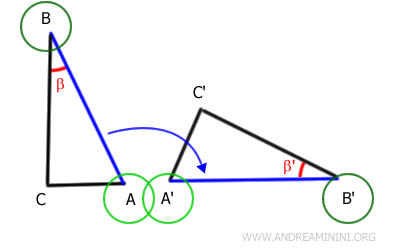
Anche gli angoli β e β' rispettivamente adiacenti ai lati AB e A'B' sono due angoli sovrapponibili. Quindi hanno la stessa ampiezza, ossia sono congruenti.

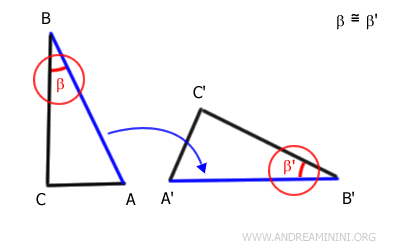
Di conseguenza, poiché l'angolo β≅β' è lo stesso, anche i lati BC e B'C' si sovrappongono perfettamente uno sull'altro.

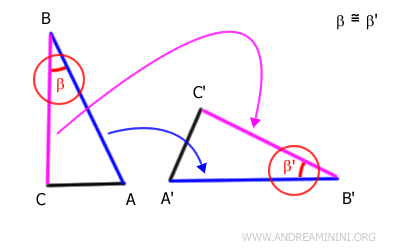
Questo vuol dire che anche gli estremi dei lati BC e B'C' si sovrappongono.

Pertanto, il punto B si sovrappone al punto B' (come già sapevo) e il punto C si sovrappone al punto C'.

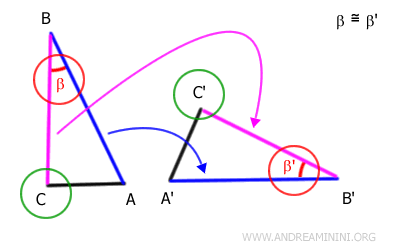
Da questo deduco che anche il segmento AC si sovrappone al segmento A'C', perché i loro estremi si sovrappongono.

In conclusione, tutti i vertici dei due triangoli si sovrappongono tra loro dopo il movimento rigido. Quindi, tutti i lati e gli angoli dei due triangoli sono ordinatamente congruenti tra loro.

Questo prova che i due triangoli sono congruenti.

E così via.