Il baricentro del triangolo

Il baricentro di un triangolo è il punto interno in cui si intersecano le sue mediane.

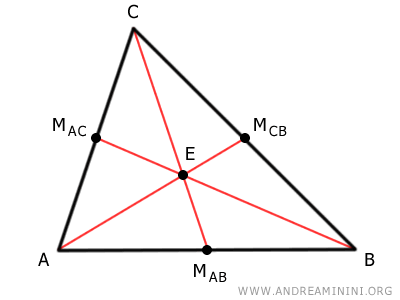
Una mediana di un triangolo è un segmento che congiunge un vertice al punto medio del lato opposto.

Ogni triangolo ha tre vertici (A, B, C) e tre lati (AB, CB, AC), quindi ha tre mediane.

Le tre mediane AM_CB, BM_AC, CM_AB si incontrano in un punto interno (E) del triangolo detto baricentro.

A cosa serve? Il baricentro è anche il punto di equilibrio del triangolo e rappresenta un punto di bilanciamento. Da questo ha origine il termine "baricentro" che deriva dal greco barys che significa "pesante" e da "centro". Ad esempio, se posizionassi il triangolo su un piccolo supporto precisamente al suo baricentro, il triangolo rimarrebbe perfettamente bilanciato ossia in equilibrio. In generale, il baricentro è molto utile per studiare il bilanciamento delle forze su una figura o un oggetto.

Come trovare il baricentro

Considero un triangolo ABC qualsiasi.

Per prima cosa individuo i punti medi di ogni lato del triangolo.

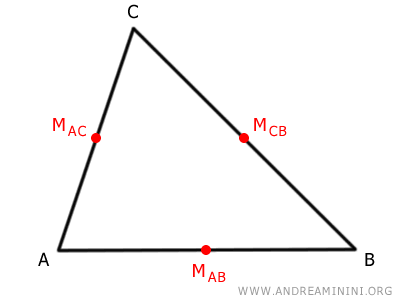
Cos'è il punto medio? Il punto medio di un segmento è il punto che lo divide in due segmenti congruenti, ossia il punto che è equidistante da entrambi gli estremi del segmento.

Disegno le tre mediane del triangolo, congiungendo ogni vertice con il punto medio che si trova sul lato opposto.

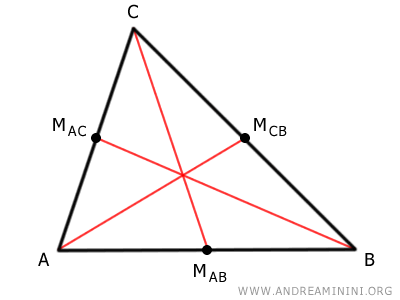
Il punto di intersezione delle mediane (E) è il baricentro del triangolo.

Il baricentro divide la mediana in due segmenti in rapporto 2:1

Il segmento dal vertice al baricentro è due volte più lungo di quello dal baricentro al punto medio del lato opposto.

Quindi, il baricentro si trova a 2/3 della lunghezza della mediana a partire dal vertice.

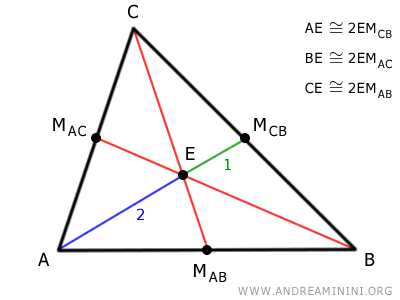
La dimostrazione

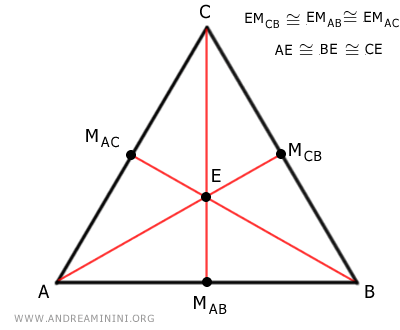
Considero un triangolo ABC.

Individuo i punti medi M e N di due lati del triangolo e traccio le relative mediane.

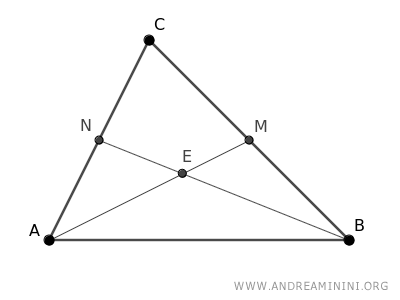
Le due mediane si incontrano nel punto E.

Individuo il punto medio dei segmenti AE e BE.

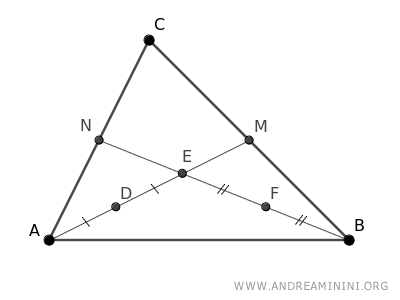
Essendo due punti medi, i segmenti AD≅ED e BF≅EF sono congruenti.

$$ \overline{AD} \cong \overline{ED} $$

$$ \overline{BF} \cong \overline{EF} $$

Traccio il segmento tra i punti medi M e N.

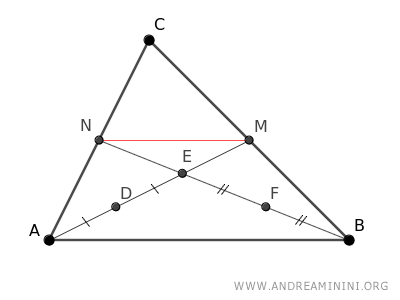
Secondo il teorema dei punti medi di un triangolo, il segmento MN che congiunge due punti medi di due lati del triangolo ABC è parallelo al terzo lato AB e ha una lunghezza pari alla metà di AB.

$$ \overline{MN} \parallel \overline{AB} $$

$$ \overline{MN} \cong \frac{1}{2} \cdot \overline{AB} $$

Traccio il segmento DF tra i due punti medi del triangolo ABE.

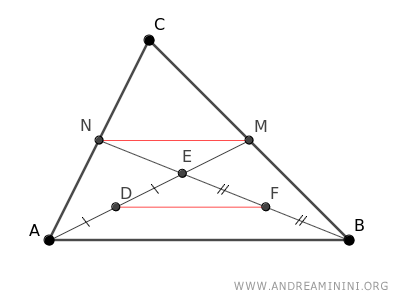
Sempre secondo il teorema dei punti medi di un triangolo, il segmento DF che congiunge due punti medi di due lati del triangolo ABE è parallelo al terzo lato AB ed è congruente alla sua metà.

$$ \overline{DF} \parallel \overline{AB} $$

$$ \overline{DF} \cong \frac{1}{2} \cdot \overline{AB} $$

Pertanto i segmenti DF e MN sono congruenti tra loro e paralleli ad AB

$$ \overline{DF} \cong \overline{MN} \cong \frac{1}{2} \cdot \overline{AB} $$

Il costrutto DFMN è un parallelogramma perché ha i lati opposti paralleli DF||MN e congruenti DF≅MN.

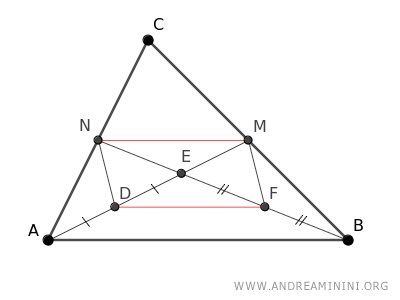
Sapendo che in un parallelogramma le diagonali si incontrano nel loro punto medio, deduco che i segmenti EN≅EF e ED≅EM sono congruenti.

$$ \overline{EN} \cong \overline{EF} $$

$$ \overline{ED} \cong \overline{EM} $$

Sapendo che ED≅AD e EF≅BF, per la proprietà transitiva EN≅EF≅BF e EM≅ED≅AD

Dal punto di vista grafico

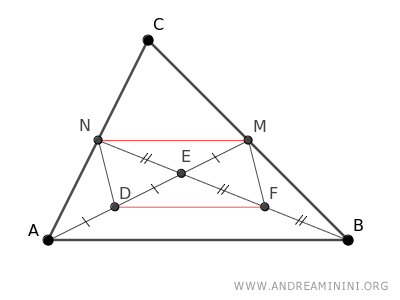
Questo vuol dire che il segmento AE è il doppio del segmento EM

$$ \overline{AE} = 2 \overline{EF} $$

Allo stesso modo, il segmento BE è il doppio del segmento EN

$$ \overline{BE} = 2 \overline{EN} $$

Questo dimostra che il baricentro divide la mediana in due segmenti in rapporto 2:1

Lo stesso ragionamento posso ripeterlo per ogni mediana del triangolo.

Il baricentro nella geometria analitica

Per trovare le coordinate del baricentro \(G(x, y)\) di un triangolo con vertici \(A(x_1, y_1)\), \(B(x_2, y_2)\), e \(C(x_3, y_3)\) in un sistema di coordinate cartesiane, posso usare le seguenti formule: $$ x = \frac{x_1 + x_2 + x_3}{3} $$ $$ y = \frac{y_1 + y_2 + y_3}{3} $$

Queste formule si ottengono facendo la media aritmetica delle coordinate \(x\) e \(y\) dei tre vertici del triangolo.

Il baricentro, dunque, si trova esattamente al "centro" del triangolo in termini di coordinate medie dei suoi vertici.

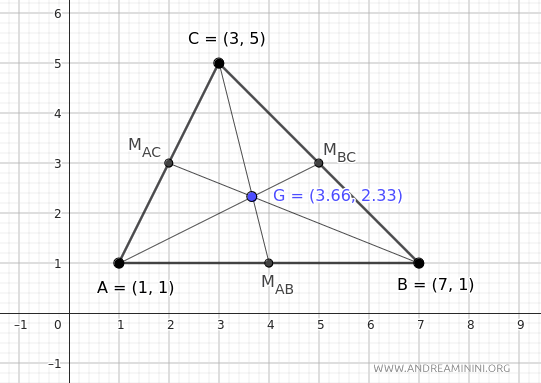
Esempio

Considero questo triangolo ABC

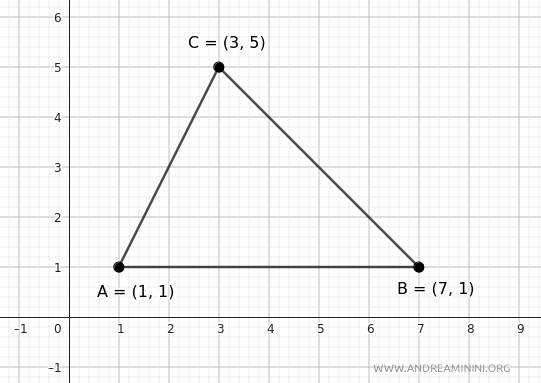
I vertici del triangolo si trovano alle coordinate cartesiane A(1;1), B(7,1), C(3;5).

$$ A(x_1; y_1)= (1;1) $$

$$ B(x_2; y_2)= (7;1) $$

$$ C(x_3; y_3)= (3;5) $$

Per trovare le coordinate del baricentro G(x;y) del triangolo applico le formule precedenti:

$$ \begin{cases} x = \frac{x_1 + x_2 + x_3}{3} \\ \\ y = \frac{y_1 + y_2 + y_3}{3} \end{cases} $$

Sostituisco le coordinate del vertice A (x₁=1,y₁=1), del vertice B (x₂=7,y₂=1) e del vertice C (x₃=3,y₃=5).

$$ \begin{cases} x = \frac{1 + 7 + 3}{3} \\ \\ y = \frac{1 + 1 + 5}{3} \end{cases} $$

$$ \begin{cases} x = \frac{11}{3} \\ \\ y = \frac{7}{3} \end{cases} $$

$$ \begin{cases} x = 3.66 \\ \\ y = 2.33 \end{cases} $$

Pertanto, il baricentro G del triangolo si trova alle coordinate (x;y)=(3.66;2.33).

Dimostrazione

Per dimostrare le formule analitiche considero un triangolo ABC.

Il baricentro G del triangolo si trova nel punto di intersezione delle mediane.

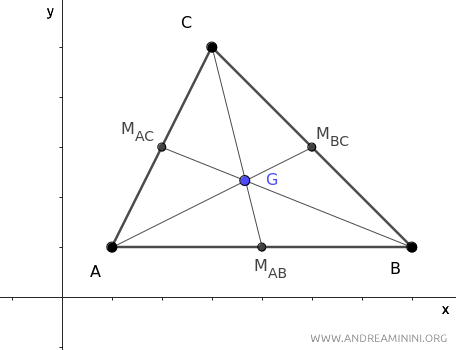
Dove ogni mediana è il segmento che congiunge un vertice del triangolo con il punto medio M del lato opposto.

Il baricentro divide ogni mediana in due parti, delle quali la parte che contiene il vertice è il doppio dell'altra.

Ad esempio, se considero la mediana AM_BC il segmento AG è il doppio del segmento GM_BC.

$$ \overline{AG} = 2 \cdot \overline{GM}_{BC} $$

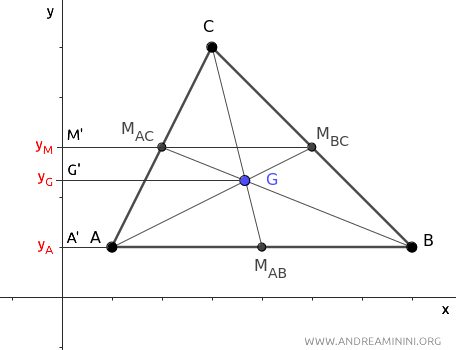
 Ora proietto i punti A, G, M_BC della mediana AM_BC sull'asse x.

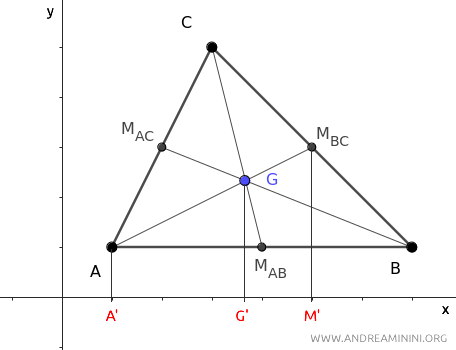
La retta A'M' è la proiezione della mediana AM_BC sull'asse x del piano cartesiano.

Le proiezioni dei punti sull'asse x sono un fascio di rette parallele che intersecano i due segmenti trasversali AM_BC e A'M'.

Secondo il teorema di Talete quando un fascio di rette parallele interseca due segmenti trasversali, i segmenti corrispondenti sulle trasversali sono direttamente proporzionali.

Quindi, se il segmento AG è il doppio di GM_BC, allora anche il segmento proiettato A'G' è il doppio di G'M'.

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

A questo punto misuro la lunghezza dei segmenti proiettati sull'asse x.

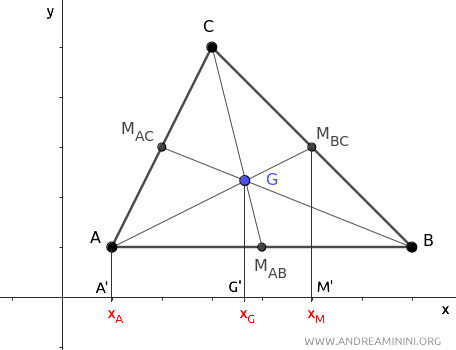
Il segmento A'G' misura x_G-x_A mentre il segmento G'M' misura x_M-x_G.

Sostituisco queste misure nell'equazione precedente:

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

$$ x_G - x_A = 2 \cdot ( x_M - x_G ) $$

$$ x_G - x_A = 2  x_M -  2x_G $$

$$ x_G +  2x_G = 2  x_M  + x_A  $$

$$ 3x_G  = 2  x_M  + x_A  $$

$$ x_G  = \frac{ 2  x_M  + x_A }{3} $$

Sapendo che il punto x_M è la proiezione del punto medio M_BC sull'asse x ovvero $ x_M = \frac{x_B+x_C}{2} $.

$$ x_G  = \frac{ 2  \frac{x_B+x_C}{2} + x_A }{3} $$

$$ x_G  = \frac{ x_A+x_B+x_C }{3} $$

Questo dimostra la formula della componente x del baricentro sul piano cartesiano.

Per dimostrare anche la componente y seguo un procedimento analogo.

Questa volta proietto i punti A, G, M_BC della mediana AM_BC sull'asse y.

Per il teorema di Talete se il segmento AG è il doppio di GM_BC, allora anche il segmento proiettato sull'asse y A'G' è il doppio di G'M'.

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

Il segmento A'G' sull'asse y misura y_G-y_A mentre il segmento G'M' misura y_M-y_G.

$$ y_G - y_A = 2 \cdot ( y_M - y_G ) $$

$$ y_G - y_A = 2 y_M - 2 y_G $$

$$ y_G + 2 y_G  = y_A + 2 y_M  $$

$$ 3y_G   = y_A + 2 y_M  $$

$$ y_G   = \frac{ y_A + 2 y_M }{3} $$

Sapendo che il punto y_M è la proiezione del punto medio M_BC sull'asse y ovvero $ y_M = \frac{y_B+y_C}{2} $.

$$ y_G   = \frac{ y_A + 2 \cdot \frac{y_B+y_C}{2} }{3} $$

$$ y_G   = \frac{ y_A + y_B+y_C }{3} $$

Questo dimostra la formula della componente y del baricentro dei triangolo sul piano cartesiano.

 

 

 

 

Osservazioni

Alcune osservazioni e proprietà sul baricentro

• Il baricentro è sempre un punto interno del triangolo.
• Esiste un solo punto di intersezione tra le mediane di un triangolo
  Per definizione il baricentro è il punto in cui si intersecano le mediane. Inoltre, è dimostrato che il baricentro divide ogni mediana nel rapporto 2:1. Sapendo che in ogni segmento esiste uno e un solo punto in grado di dividerlo nel rapporto 2:1, una volta noto che il punto E di una mediana AM_CB divide quest'ultima nel rapporto 2:1, lo stesso punto E deve dividere anche le altre mediane del triangolo nello stesso rapporto. Non possono esserci altri punti. In conclusione, esiste solo un punto in cui le mediane sono divisibili nel rapporto 2:1 ed è il punto di intersezione tra le stesse.
  
• Il baricentro è il centro di gravità del triangolo
  In altre parole, è un punto di equilibrio. Ad esempio, se poggiassi il triangolo su un chiodo esattamente nel suo baricentro, il triangolo resterebbe in equilibrio.

  Nota. La conoscenza del baricentro mi permette conoscere il centro di gravità di una forma e mi aiuta a determinare come si distribuiscono le forze.

• Qualsiasi movimento rigido (es. rotazione, traslazione) non modifica la posizione interna del baricentro. Il baricentro si sposta o ruota con il triangolo.
• Nel caso particolare del triangolo equilatero il baricentro coincide con l'incentro, il circocentro e l'ortocentro.
  

E così via.