Il primo teorema di Euclide
In un triangolo rettangolo il quadrato costruito su un cateto è equivalente, ossia ha la stessa area, del rettangolo costruito sulla proiezione dello stesso cateto sull'ipotenusa che ha l'altezza congruente con l'ipotenusa.
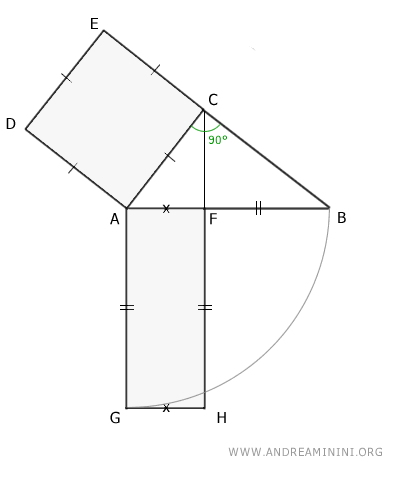
In altre parole, se proietto i cateti AC o BC di un triangolo rettangolo sull'ipotenusa AB, ottengo due segmenti AF e BF, tali che:
$$ \overline{AF} + \overline{BF} = \overline{AB} $$
Il teorema di Euclide afferma che l'area del quadrato costruito su AC che è AC2 è uguale all'area AB·AF del rettangolo formato da AB e AF.
$$ \overline{AC}^2 = \overline{AB} \cdot \overline{AF} $$
Analogamente lo stesso vale per l'altro cateto.
Nota. Il primo teorema di Euclide si concentra sulle relazioni di proporzionalità tra i lati del triangolo rettangolo, le proiezioni dei cateti sull'ipotenusa e l'ipotenusa stessa. Si distingue dal teorema di Pitagora che, invece, stabilisce una relazione di uguaglianza tra le aree: la somma delle aree dei quadrati costruiti sui cateti è uguale all'area del quadrato costruito sull'ipotenusa.
Come corollario si può anche affermare che in un triangolo rettangolo ogni cateto è medio proporzionale fra l'ipotenusa e la sua proiezione sull'ipotenusa
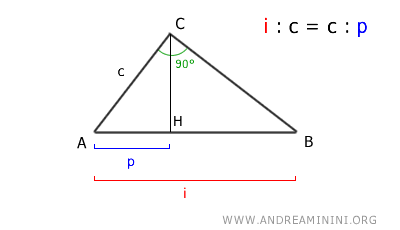
In altre parole, l'ipotenusa (i) sta al cateto (c) come il cateto (c) sta alla sua proiezione (p) sull'ipotenusa.
Nota. La proporzione i:c=c:p è del tutto equivalente al primo teorema di Euclide $$ i : c = c : p \rightarrow c^2 = i \cdot p $$ Sono due modi diversi per dire la stessa cosa.
Un esempio pratico
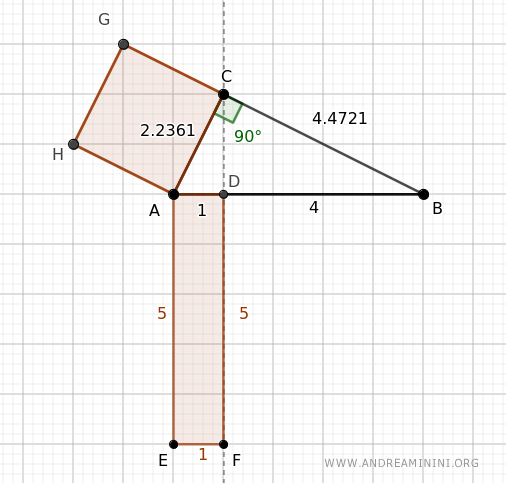
Prendo come esempio un triangolo rettangolo con queste misure AB=5, BC=4.4721 e AC=2.2361
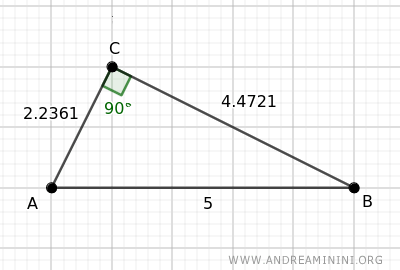
Proietto il cateto AC sull'ipotenusa AB.
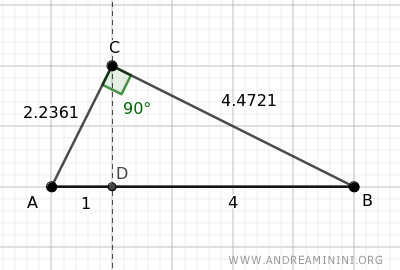
La proiezione ha diviso l'ipotenusa AB=5 in due segmenti AD=1 e BD=4.
A questo punto calcolo l'area del quadrato costruito sul cateto AC
$$ \overline{AC}^2 = 2.2361^2 = 5 $$
Poi calcolo l'area del rettangolo costruito sulla proiezione del cateto AC sull'ipotenusa, ovvero AD=1, che ha una lunghezza pari all'ipotenusa stessa AB=5.
$$ \overline{AD} \cdot \overline{AB} = 1 \cdot 5 = 5 $$
L'area è la stessa, come previsto dal teorema di Euclide.
Esempio 2
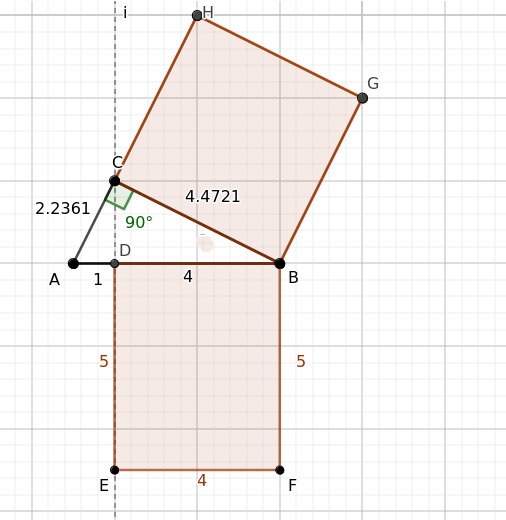
Per ultimare l'esempio calcolo il quadrato anche sull'altro cateto BC.

In questo caso il quadrato costruito sul lato BC=4.4721
$$ \overline{BC}^2 = 4.4721^2 = 20 $$
Poi calcolo l'area del rettangolo che ha per base la proiezione del cateto BC sull'ipotenusa, ovvero BD=4, e per lunghezza l'ipotenusa stessa AB=5.
$$ \overline{BD} \cdot \overline{AB} = 4 \cdot 5 = 20 $$
Anche in questo caso il risultato è lo stesso.
La dimostrazione
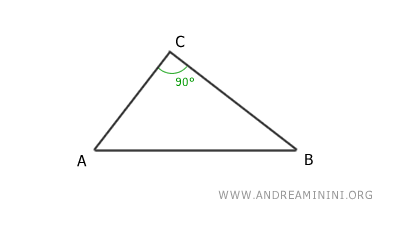
Considero un triangolo rettangolo ABC.
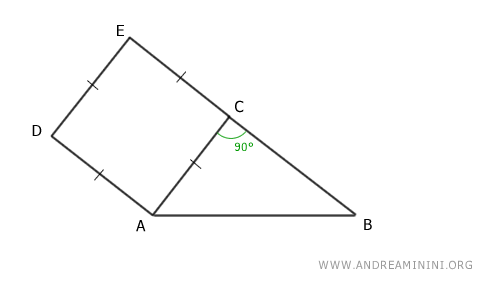
Costruisco un quadrato ACED su un cateto AC.
Proietto il cateto AC sull'ipotenusa AB che viene suddivisa in due segmenti AF e BF.
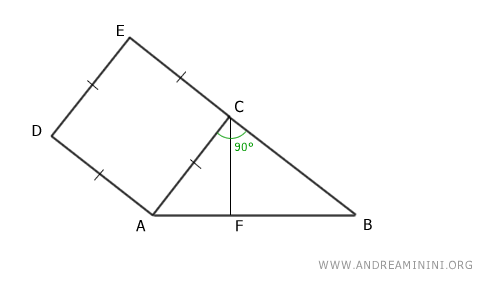
Costruisco un rettangolo sulla proiezione del cateto sull'ipotenusa, con un lato laterale lungo come l'ipotenusa.
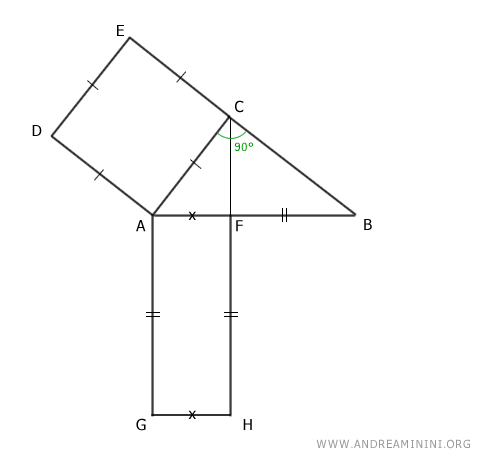
Quindi, questo rettangolo ha i lati laterali congruenti con l'ipotenusa.
$$ \overline{AF} \cong \overline{AG} \cong \overline{FH} $$
Disegno le rette passanti per i lati del rettangolo e la retta passante per il lato del quadrato opposto al cateto.
Indico i punti di intersezione con K e L.
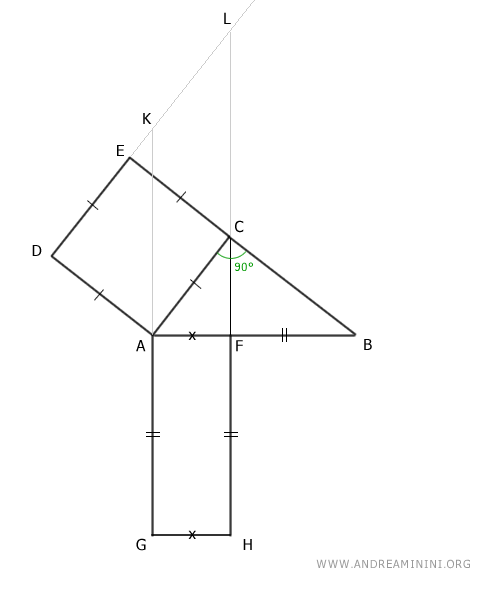
Osservo gli angoli del quadrato sul cateto AC e rispetto all'ipotenusa.
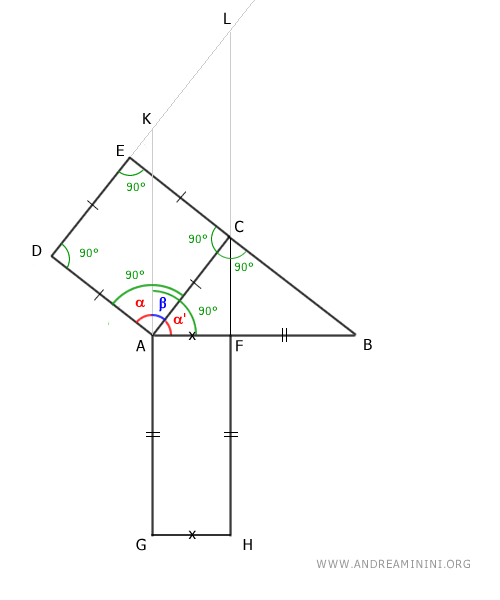
Gli angoli α e α' sono congruenti α≅α' perché sono entrambi complementari dell'angolo β, in quanto il quadrato e il rettangolo hanno tutti gli angoli retti (90°).
$$ \alpha + \beta = 90° $$
$$ \alpha ' + \beta = 90° $$
Quindi, sono congruenti
$$ \alpha + \beta = \alpha ' + \beta $$
$$ \alpha = \alpha ' $$
I triangoli AKD e ABC sono triangoli congruenti per il secondo principio di congruenza dei triangoli perché hanno un lato congruente AC≅AD e gli angoli adiacenti congruenti 90° e α≅α'.
$$ AKD \cong ABC $$
Essendo triangoli congruenti, i triangoli AKD e ABC hanno tutti i lati e gli angoli congruenti.
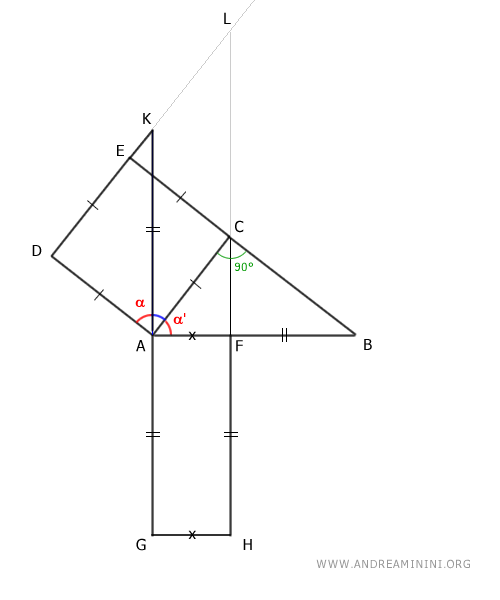
In particolar modo mi interessa sapere che sono congruenti i lati AK e AB
$$ \overline{AK} \cong \overline{AB} $$
Ora, per costruzione il quadrilatero ACLK è un parallelogramma perché ha i lati opposti paralleli.
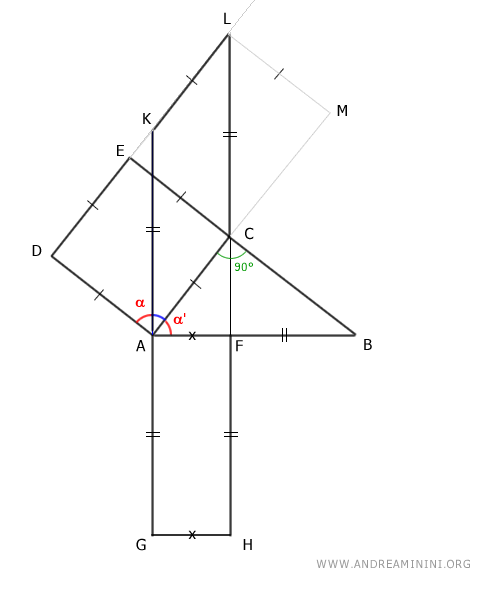
Secondo il principio di equivalenza dei parallelogrammi, il quadrato ACED e il parallelogramma ACLK sono equivalenti, possiedono la stessa area, perché hanno la stessa base AC e l'altezza congruente EA≅LM
$$ ACED \doteq ACLK $$
Per lo stesso motivo sono equivalenti anche il rettangolo AFHG e il parallelogramma ACLK, perché hanno la base congruente AG≅AK e la stessa altezza AH.
$$ AFHG \doteq ACLK $$
Di conseguenza per la proprietà transitiva sono equivalenti anche il quadrato ACED e il rettangolo AFHG.
$$ ACED \doteq ACLK \doteq AFHG $$
$$ ACED \doteq AFHG $$
Pertanto, l'area del quadrato costruito sul cateto AC è uguale all'area del rettangolo costruito sulla proiezione del cateto AC sull'ipotenusa che ha per lato l'ipotenusa stessa.
Questo dimostra il teorema di Euclide dei triangoli rettangoli.
Nota. Allo stesso modo si può dimostrare che la stessa proprietà vale anche per l'altro cateto BC del triangolo rettangolo.
Corollario
In un triangolo rettangolo ogni cateto (c) è il medio proporzionale fra l'ipotenusa (i) e la sua proiezione (p) sull'ipotenusa

In altre parole, l'ipotenusa sta al cateto come il cateto sta alla sua proiezione sull'ipotenusa.
$$ i:c = c:p $$
Questo significa che il quadrato del cateto (c) è uguale al prodotto tra l'ipotenusa (i) e la proiezione (p) del cateto sull'ipotenusa.
$$ \frac{i}{c} = \frac{c}{p} $$
$$ c^2= i \cdot p $$
Si ritorna così al primo teorema di Euclide, in base al quale l'area del quadrato costruito sul cateto del triangolo rettangolo è uguale all'area del rettangolo costruito sulla proiezione del cateto stesso e l'ipotenusa.

Esempio
Riprendo l'esempio precedente del triangolo rettangolo ABC di cui conosco già tutte le misure

Il cateto AC misura approssimativamente 2.2361, la sua proiezione sull'ipotenusa (AD) misura 1 e l'ipotenusa AB misura 5.
In base al corollario, il cateto AC è medio proporzionale tra l'ipotenusa AB e la sua proiezione AD sull'ipotenusa.
$$ \overline{AB} : \overline{AC} = \overline{AC} = \overline{AD} $$
Sostituisco i valori delle lunghezze corrispondenti dei segmenti
$$ 5 : 2.2361 = 2.2361 : 1 $$
Nella proporzione la lunghezza del cateto (2.2361) è il medio proporzionale.
La proporzione è soddisfatta, salvo qualche imprecisione dovuta all'arrotondamento delle cifre decimali del lato AC da parte di Geogebra.
$$ 2.2361 = 2.2361 $$
Lo stesso vale se considero l'altro cateto BC del triangolo rettangolo.
Nonostante le piccole imprecisioni dovute all'arrotondamento, dovute a Geogebra, l'esempio dimostra la validità del corollario usando delle misure reali.
La dimostrazione
Considero il triangolo rettangolo ABC e il cateto AC.
Il segmento AH è la proiezione del cateto AC sull'ipotenusa AB.
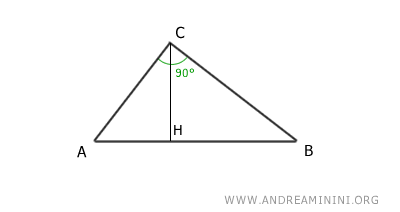
Per il primo criterio di similitudine dei triangoli, i triangoli ABC e AHC sono triangoli simili perché hanno due angoli congruenti nello stesso ordine: un angolo retto (90°) e un angolo coincidente (α).
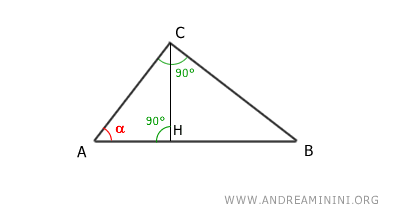
Nota. Se i triangoli hanno due angoli congruenti, di conseguenza anche il terzo angolo è congruente, essendo la somma degli angoli interni di un triangolo sempre uguale a 180°
Pertanto, i triangoli ABC e AHC sono simili.
$$ ABC \approx AHC $$
Essendo due triangoli simili hanno tutti i lati ordinatamente proporzionali.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AH} = \overline{CB} : \overline{CH} $$
Questo dimostra il corollario, ovvero l'ipotenusa (AB) sta al cateto (AC) come quest'ultimo sta alla sua proiezione (AH) sull'ipotenusa.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AH} $$
E così via.
