Tangente
Nella circonferenza goniometrica la tangente di un angolo alfa è il rapporto tra il seno e il coseno dell'angolo alfa. $$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$ Si indica con il simbolo tan o tg.
Il termine "tangente" deriva dal latino "tangere" ossia "toccare".
Dal punto di vista geometrico la tangente è il segmento perpendicolare all'asse x che ha origine nel punto C e interseca il prolungamento del lato OP.
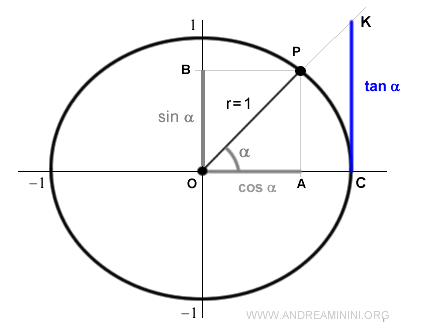
Dimostrazione. Preso un angolo α si formano due triangoli simili OAP e OCK. Quindi, posso scrivere la proporzione tra i segmenti $$ \overline{ KC } \ : \ \overline{ PA } = \overline{ OC } \ : \ \overline{ OA } $$ ossia $$ \frac{ \overline{ KC } }{\ \overline{ PA } } = \frac{ \overline{ OC } } { \overline{ OA } } $$ Poiché una circonferenza goniometrica ha raggio unitario posso sostituire OC=1 $$ \frac{ \overline{ KC } }{\ \overline{ PA } } = \frac{ 1 } { \overline{ OA } } $$ Metto in evidenza il segmento della tangente KC $$ \overline{ KC } = \frac{ \overline{ PA } } { \overline{ OA } } $$ Dove PA è il seno dell'angolo α mentre OA è il coseno dell'angolo α. $$ \overline{ KC } = \frac{ \sin \alpha } { \cos \alpha } $$ Sapendo che anche tan α=sin α/cos α questo dimostra l'equivalenza tra il segmento KC e la tangente dell'angolo α. $$ \overline{ KC } = \frac{ \sin \alpha } { \cos \alpha } = tan \ \alpha$$
La tangente è una funzione periodica con periodo [ 0 ; π ).
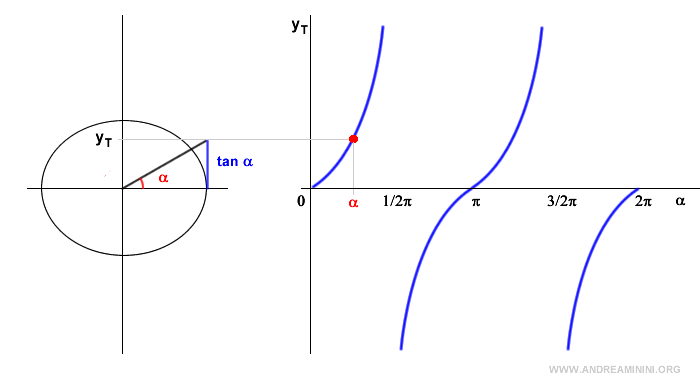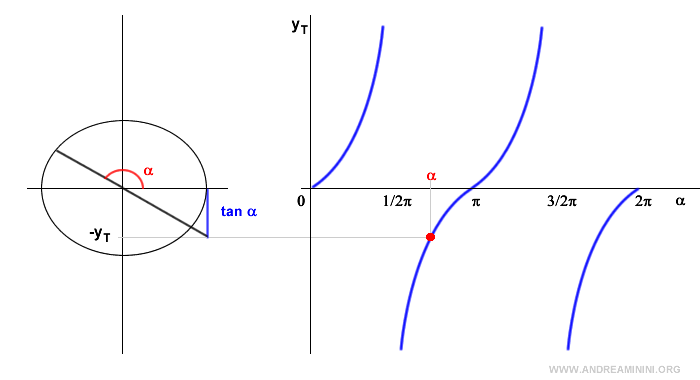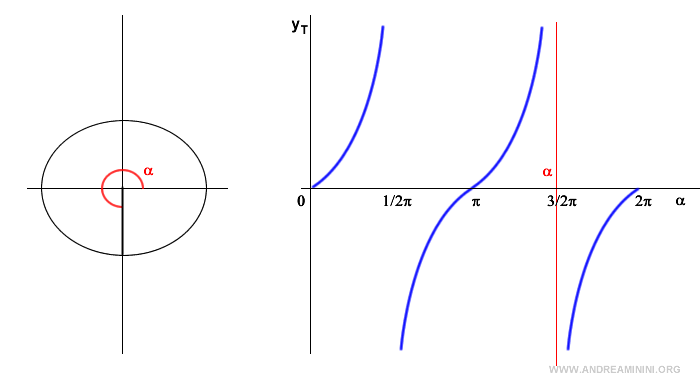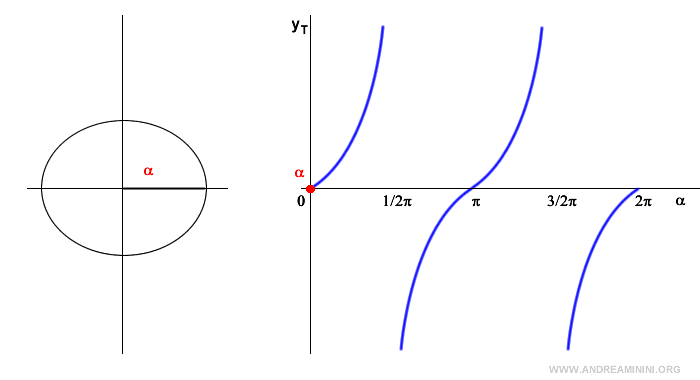
Nota. Nel primo quadrante la tangente è positiva e tende a infinito quando l'angolo orientato tende a 90°. Quando l'angolo è pari a 90° la tangente non esiste perché il coseno è zero. Nel secondo quadrante la tangente è negativa perché il coseno è negativo mentre il seno è positivo. Nel terzo quadrante la tangente è positiva perché sia il seno che il coseno sono valori negativi. Quando l'angolo è pari a 270° la tangente non esiste perché il coseno è zero. Nel quarto quadrante la tangente è negativa perché il seno è negativo mentre il coseno è positivo.
In π/2 (90°) e 3/2π (270°) la tangente non esiste.
In questi punti si formano due asintoti verticali.
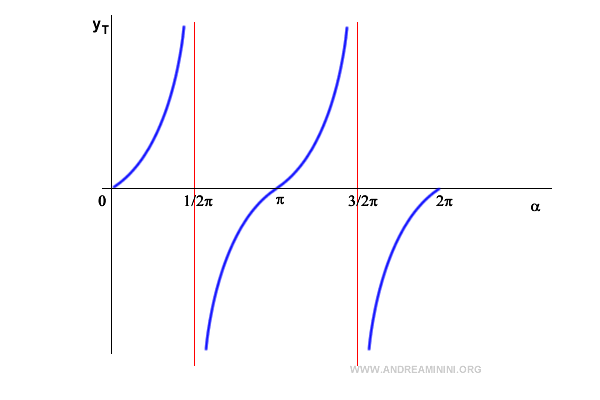
Essendo una funzione periodica la tangente ha infiniti asintoti nei punti
$$ \frac{ \pi }{ 2 } + k \cdot \pi \ \ \ \ k \in Z $$
Pertanto il dominio della funzione tangente è l'insieme dei numeri reali R ridotto dei punti in cui la tangente non è definita.
$$ R - \{ \frac{ \pi }{ 2 } + k \cdot \pi \} $$
Il codominio della tangente, invece, varia da -∞ a +∞. Quindi comprende l'intero insieme dei numeri reali R.
$$ \tan \ \alpha \ \ : \ \ R - \{ \frac{ \pi }{ 2 } + k \cdot \pi \} \longrightarrow (-∞ ; +∞ ) $$
A differenza del seno e del coseno la tangente può assumere qualsiasi valore reale.
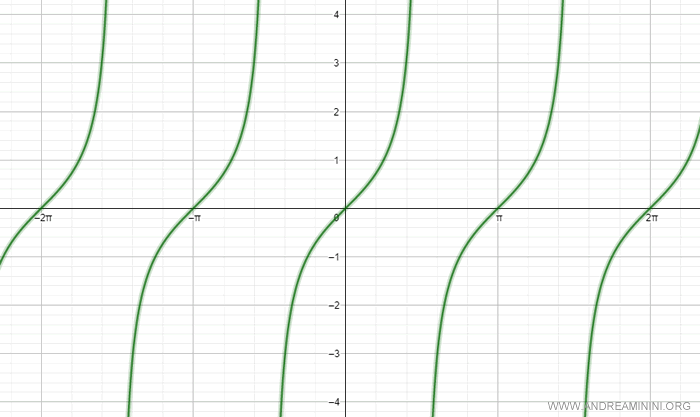
Nota. Il grafico completo della tangente per qualsiasi angolo orientato si chiama tangentoide.
La tangente è una funzione periodica che si ripete dopo ogni periodo π (ossia 180°).
$$ \tan \alpha = \tan( \alpha + n \cdot \pi ) $$
Non è una funzione continua perché nel grafico ci sono infiniti punti di discontinuità in corrispondenza degli asintoti verticali.
La tangente non è definita nell'angolo π/2 (ossa 90°) e in ogni angolo periodico π/2 ± n·π.
$$ \alpha = \frac{\pi}{2} \pm n \cdot \pi $$
Nota. Il rapporto sin/cos non esiste quando il denominatore è nullo, ossia quando il coseno è zero. La funzione coseno è nulla per π/2 ( 90° ) e per ogni altro valore ottenuto aggiungendo a π/2 un multiplo intero k di angolo piatto π ossia π/2+k·π ( ovvero 90°+k·180° ). $$ \cos (\frac{\pi}{2}+k \cdot \pi) \ \ \ \ k \in Z $$
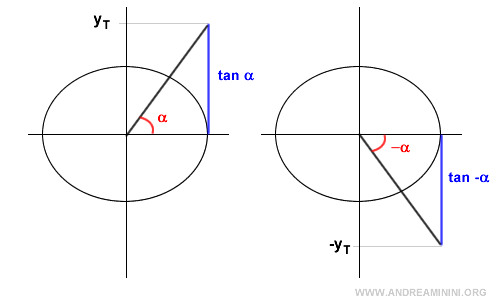
La tangente è una funzione dispari perché tan(-α) = - tan(α)
$$ \tan ( - \alpha ) = - \tan ( \alpha ) $$
Le funzione tangente di un angolo orientato (α) e del suo opposto (-α) hanno lo stesso valore ma segno diverso
Gli angoli fondamentali
Ecco alcuni angoli importanti delle funzioni tangente
| angolo (gradi) | angolo (radianti) | tangente |
|---|---|---|
| $$ 0° $$ | $$ 0 $$ | $$ 0 $$ |
| $$ 30° $$ | $$ \frac{\pi}{6} $$ | $$ \frac{\sqrt{3}}{3} $$ |
| $$ 45° $$ | $$ \frac{\pi}{4} $$ | $$ 1 $$ |
| $$ 60° $$ | $$ \frac{\pi}{3} $$ | $$ \sqrt{3} $$ |
| $$ 90° $$ | $$ \frac{\pi}{2} $$ | $$ \nexists $$ |
| $$ 180° $$ | $$ \pi $$ | $$ 0 $$ |
| $$ 270° $$ | $$ \frac{3 \pi}{2} $$ | $$ \nexists $$ |
La tangente è una funzione periodica di periodo π.
La funzione inversa della tangente
La tangente non è invertibile perché non è una funzione biettiva (biunivoca).

Tuttavia, se considero la riduzione del dominio nell'intervallo [-π/2, π/2] anche la tangente diventa biettiva.
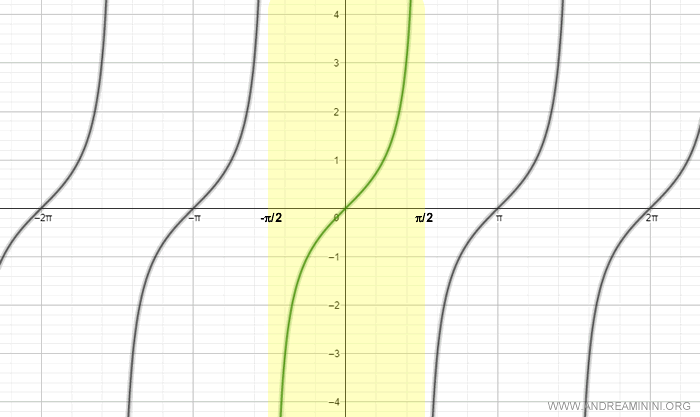
Quindi, nell'intervallo [-π/2, π/2] la tangente è una funzione invertibile.
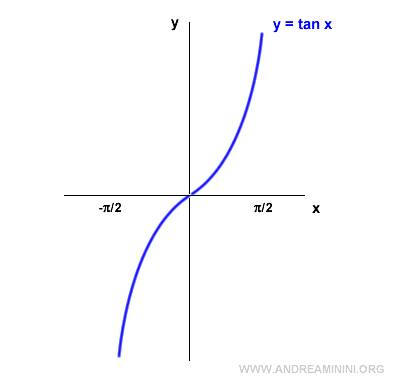
Per trovare il grafico della funzione inversa della tangente, ruoto il grafico di 90° in senso antiorario.
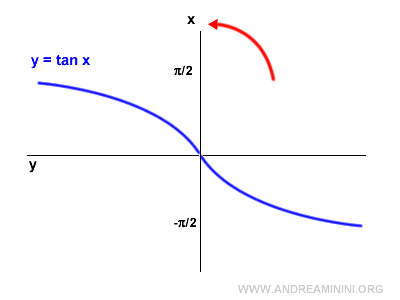
Poi rifletto il grafico in orizzontale.
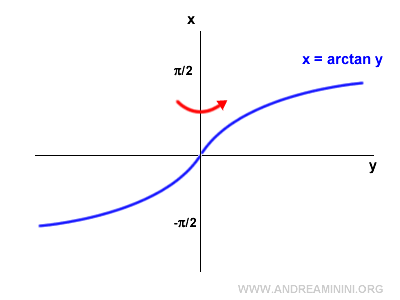
La funzione inversa della tangente è l'arcotangente (arctan).
Nota. Posso invertibile la tangente anche in intervalli diversi da [-π/2,π/2] purché la funzione tangente sia biettiva. Ad esempio, anche nell'intervallo [π/2,3π/2] la tangente è invertibile.
L'origine della parola tangente
Il termine "tangente" venne introdotto dal matematico e fisico danese Thomas Fincke nel XVI secolo in riferimento agli orologi solari.
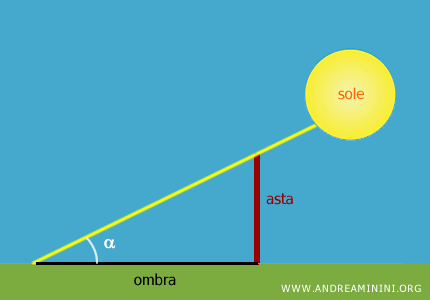
In un orologio solare un'asta (gnomone) proietta l'ombra del sole sul terreno con un angolo alfa.
Il rapporto fra la lunghezza dell'asta e dell'ombra è la tangente dell'angolo alfa.
E così via.
