Triangolo equilatero

Un triangolo è detto triangolo equilatero se ha tutti i tre lati congruenti.

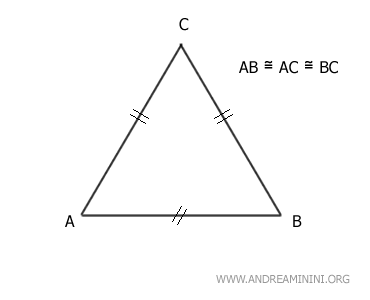
In altre parole, un triangolo equilatero ha tre lati della stessa lunghezza.

Il termine "equilatero" deriva dal latino e significa "lato uguale".

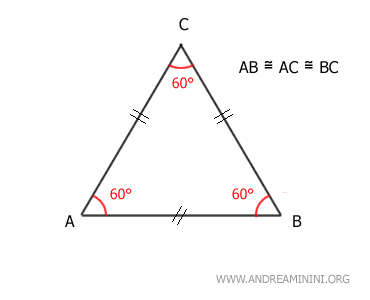
Un'altra caratteristica distintiva dei triangoli equilateri è di avere anche tutti gli angoli congruenti, perché ogni angolo ha un'ampiezza pari a 60°. In ogni triangolo la somma degli angoli è pari a 180° ossia 60°+60°+60°.

Le formule

Le principali formule per calcolare le misure di un triangolo equilatero:

• Perimetro
  Basta moltiplicare per tre la lunghezza di un lato $$ P = 3 l $$
• Area
  Come ogni triangolo si può ottenere moltiplicando la base (b) per l'altezza (h) diviso due. $$ A = \frac{b \cdot h}{2} $$ Nel caso particolare dei triangoli equilateri posso usare anche questa formula $$ A = \frac{l^2 \cdot √3}{4} $$
• Lato
  Posso trovare la lunghezza del lato conoscendo l'altezza (h) del triangolo equilatero tramite la formula seguente ( dimostrazione )  $$ l = \frac{2h}{ \sqrt{3} } $$ In alternativa, il lato di un triangolo equilatero è uguale al raggio (r) del cerchio circoscritto al triangolo per la radice quadrata di tre ( vedi dimostrazione ). $$ l = r \cdot \sqrt{3} $$ Il lato del triangolo equilatero si può ottenere anche a partire dal raggio del cerchio inscritto nel triangolo (dimostrazione) $$ l = 2r \sqrt{3}  $$ 
• Altezza
  La formula per ottenere l'altezza deriva dalla formula del lato ( dimostrazione ) $$ h = \frac{l}{ 2} \sqrt{3} $$

Nota. Il fatto che in un triangolo equilatero i lati sono congruenti permette di calcolare l'area e il perimetro usando delle formule alternative tramite l'applicazione del teorema di Pitagora a una metà del triangolo equilatero.

Come disegnare un triangolo equilatero

Per costruire un triangolo equilatero traccio un segmento AB.

Poi punto il compasso nell'estremo A e con raggio AB traccio un primo arco.

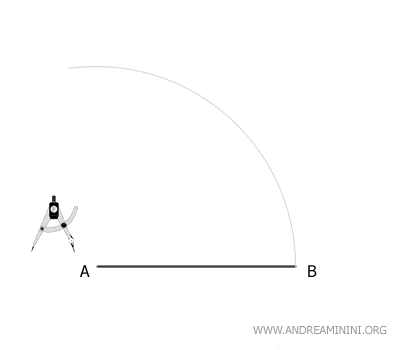
Mantenendo la stessa apertura del compasso (raggio AB) centro il compasso sul secondo estremo e traccio un secondo arco.

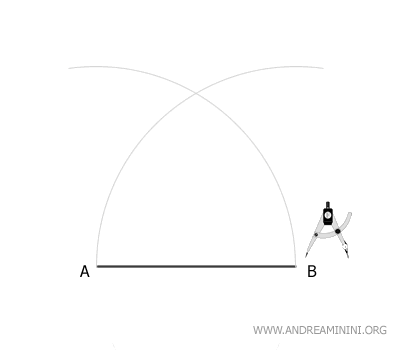
I due archi si intersecano nel punto C.

Ho così individuato il terzo vertice del triangolo equilatero.

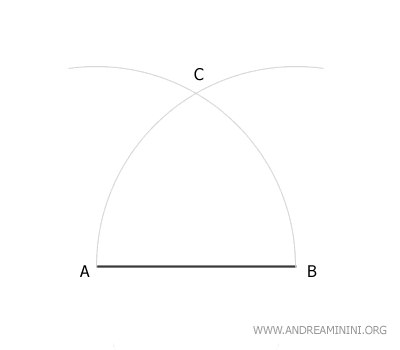
Traccio due segmenti AC e BC.

Il risultato finale è un triangolo equilatero.

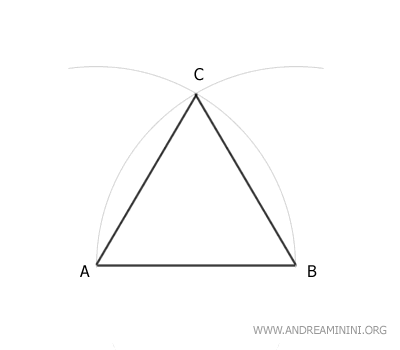
Tutti i lati del triangolo sono congruenti ossia hanno la stessa lunghezza.

Per vedere altre tecniche di costruzione del triangolo equilatero clicca qui.

Osservazioni sui triangoli equilateri

I triangoli equilateri hanno le seguenti caratteristiche

• Un triangolo equilatero è un triangolo isoscele con tre basi
  Un triangolo è isoscele se ha due lati congruenti (AC≅BC). Il lato rimanente (AB) è la base e ha due angoli congruenti (α≅β).
  
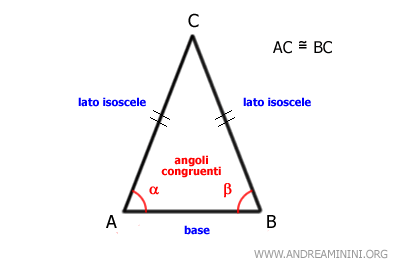
  Il triangolo equilatero ha tre lati congruenti (AC≅BC≅AB).. Quindi, tutti i lati possono essere considerati come base e i restanti due come lati isoscele.
  
  Pertanto, i triangoli equilateri sono un sottoinsieme dei triangoli isoscele in cui la base è congruente ai lati isoscele.

  Questo aspetto è molto importante perché mi permette di dimostrare molte caratteristiche del triangolo equilatero usando gli stessi teoremi del triangolo isoscele.

• Gli angoli del triangolo equilatero sono congruenti
  In un triangolo equilatero tutti e tre gli angoli sono congruenti.
  

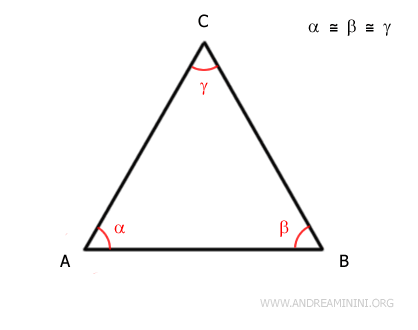
  Dimostrazione. Un triangolo equilatero posso considerarlo come un triangolo isoscele con tre basi. In un triangolo isoscele gli angoli alla base sono congruenti (teorema del triangolo isoscele).
  
  In un triangolo equilatero ci sono tre basi.
  
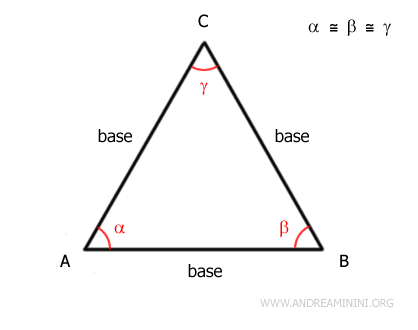
  Quindi, sapendo che gli angoli alle basi sono congruenti $$ \alpha = \beta $$ $$ \beta = \gamma $$ $$ \alpha = \gamma $$ Per la proprietà transitiva deduco che $$ \alpha = \beta = \gamma $$ Pertanto, in un triangolo equilatero tutti gli angoli sono congruenti.

• Gli angoli del triangolo equilatero misurano 60°
  In un triangolo equilatero ogni angolo ha un'ampiezza di 60 gradi
  

  Dimostrazione. La somma degli angoli di un triangolo è sempre uguale a 180°. Sapendo che in un triangolo equilatero tutti e tre gli angoli sono congruenti, basta dividere 180° per tre. $$ 180° \ : \ 3 = 60° $$

• In un triangolo equilatero ogni bisettrice è anche mediana e altezza
  Le altezze, le mediane, le bisettrici e le bisettrici perpendicolari tracciate da un vertice qualsiasi al centro del lato opposto coincidono tutte nello stesso segmento, chiamato asse del triangolo.
  
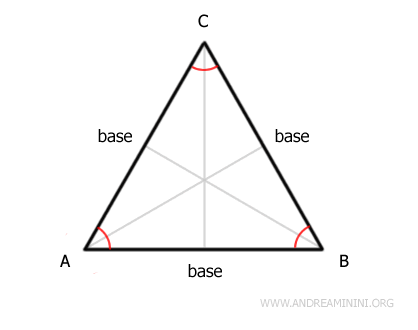
  Pertanto, in un triangolo equilatero il baricentro coincide con l'incentro, il circocentro e l'ortocentro.

  Dimostrazione. Un triangolo equilatero è un triangolo isoscele con tre basi diverse. Quindi, posso applicare al triangolo equilatero gli stessi teoremi di quello isoscele. In particolar modo, mi basta ricordare che in un triangolo isoscele la bisettrice di un triangolo isoscele è anche l'altezza e la mediana rispetto alla base.
  
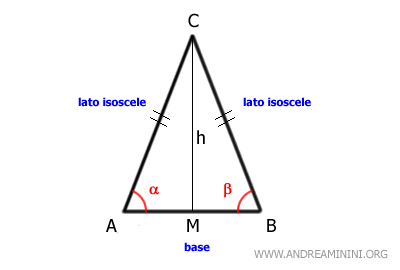
  In un triangolo equilatero ci sono tre basi, quindi tutte le bisettrici sono anche altezza e mediana rispetto alla propria base.
  

• Ogni angolo di un triangolo equilatero è la terza parte di un angolo piatto

  Dimostrazione. Per il teorema della somma degli angoli interni, in un triangolo la somma degli angoli interni è congruente a un angolo piatto (180°) $$ \alpha + \beta + \gamma = 180° $$ Sapendo che gli angoli interni di un triangolo interno sono congruenti, ogni angolo è la terza parte di un angolo piatto (180°). $$ \alpha = \beta = \gamma = \frac{180°}{3} = 60° $$

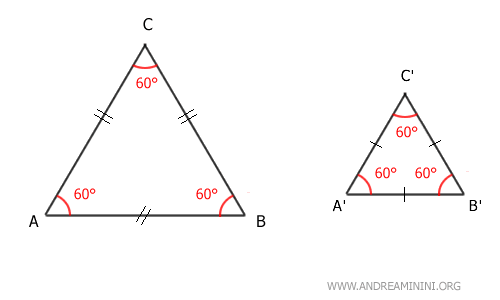
• Due triangoli equilateri sono triangoli simili
  Due triangoli equilateri, anche di dimensioni differenti, hanno sempre gli angoli corrispondenti congruenti. Pertanto, in base al primo principio di similitudine dei triangoli, i due triangoli equilateri sono triangoli simili.
  
• Nel caso del triangolo equilatero non posso tracciare la retta di Eulero perché il baricentro, il circocentro e l'ortocentro un unico punto, quindi non sono allineati. Al suo posto esiste un fascio di infinite rette passanti per lo stesso punto.
• L'area di un triangolo equilatero può essere calcolata utilizzando la formula:
  $$ A = \frac{l^2 \cdot √3}{4} $$ dove l è la lunghezza di un lato.
• Il lato del triangolo equilatero è uguale al raggio del cerchio circoscritto per √3 $$ l = r \cdot \sqrt{3} $$

  Il raggio del cerchio circoscritto che tocca tutti e tre i vertici del triangolo è uguale a (l/√3), dove l è la lunghezza di un lato del triangolo. $$ r = \frac{l}{\sqrt{3}} $$
  
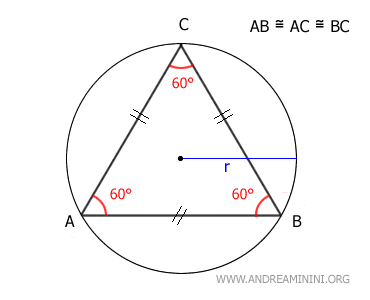
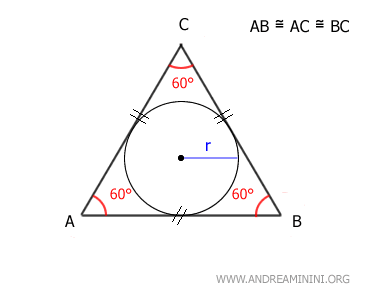
  Pertanto, il lato del triangolo equilatero è uguale al raggio del cerchio circoscritto per √3 $$ l = r \cdot \sqrt{3} $$

• Il raggio del cerchio inscritto che tocca tutti e tre i lati del triangolo è uguale a (l/2√3), dove l è la lunghezza di un lato del triangolo. $$ r = \frac{l}{2 \cdot \sqrt{3}} $$ Di conseguenza, il lato del triangolo equilatero si può ottenere anche a partire dal raggio del cerchio inscritto. $$ l = 2 \sqrt{3}  \cdot r $$
  
• La relazione tra la circonferenza inscritta e circoscritta
  In un triangolo equilatero c'è una relazione costante tra il raggio della circonferenza inscritta (indicata con \(r\)) e quello della circonferenza circoscritta (indicata con \(R\)). Questa relazione è espressa dalla formula: $$ r = \frac{1}{2} \cdot R $$ Questo accade perché in un triangolo equilatero tutti i punti notevoli ( baricentro, ortocentro, circocentro e incentro ) coincidono in un unico punto (O).
  
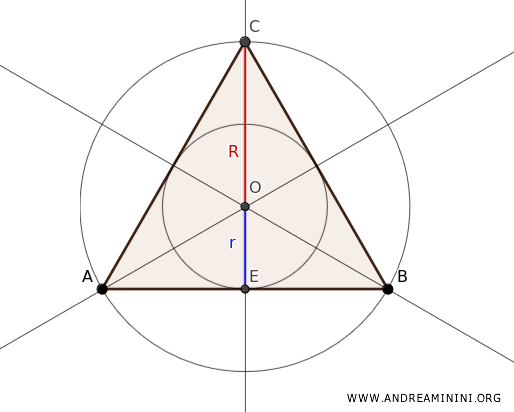
  In particolar modo il circocentro e l'incentro sono situati nello stesso punto, quindi il cerchio inscritto e quello circoscritto hanno lo stesso centro ma raggio differente. Sapendo che il baricentro divide ogni mediana (es, EC) in due segmenti, uno doppio rispetto all'altro, da questo posso dedurre che il raggio della circonferenza circoscritta \(R\) è il doppio del raggio della circonferenza inscritta \(r\), ovvero $ R = 2r $ L'altezza del triangolo equilatero \(ABC\) posso esprimerla come somma dei due raggi $ h = r + R $ Sostituendo \(R = 2r\) nella formula precedente, ottengo $ h = r + 2r = 3r $. Quindi, sapendo che $ h = r + R $ e $ h=3r $ si deduce che $ 3r = r + R $ ovvero $ 2r = R $. Questo conferma che \(r = \frac{1}{2}R\).

Queste proprietà valgono solo per i triangoli equilateri.

E così via.