I criteri di congruenza dei triangoli
I tre criteri di congruenza dei triangoli permettono di stabilire se due triangoli sono congruenti, conoscendo solo alcune informazioni su di essi.
In generale, secondo la definizione di congruenza, due figure geometriche sono congruenti quando sono sovrapponibili punto a punto tramite un movimento rigido.
Questa semplice regola di congruenza vale anche per i triangoli ma è molto impegnativa, perché richiede la conoscenza di tutte le informazioni.
Nel caso dei triangoli esistono anche tre criteri di congruenza per verificare se due triangoli sono congruenti, usando soltanto tre informazioni su di essi.
Perché usare i criteri di congruenza? I criteri di congruenza dei triangoli confrontano coppie di lati e di angoli, evitando così di dover confrontare tutte le coppie di punti. Quindi, sono più rapidi e si basano solo su alcune informazioni disponibili.
Il primo criterio di congruenza dei triangoli
Due triangoli sono congruenti se hanno congruenti nello stesso ordine due lati e l'angolo compreso tra di essi.
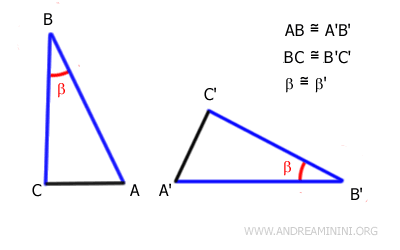
In pratica, i triangoli sono congruenti se hanno due lati della stessa lunghezza e l'angolo tra di essi della stessa ampiezza.
E' anche conosciuto come criterio LAL (Lato-Angolo-Lato)
Tuttavia, il termine LAL non va preso alla lettera perché è necessario che l'angolo sia compreso tra i lati.
Se l'angolo congruente non è quello compreso tra i due lati, non è detto che il triangolo sia congruente.
Ad esempio, considero il triangolo ABC. Traccio un cerchio con raggio AC e centro A. L'arco interseca il prolungamento del segmento AC nel puntoi D. Questo mi permette di ottenere un altro triangolo ACD.
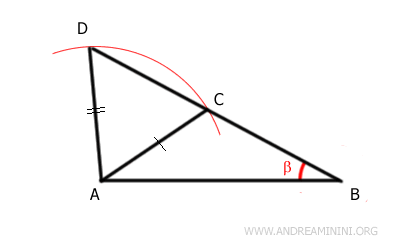
I due triangoli ABC e ABD non sono congruenti. Tuttavia, hanno due lati congruenti AB≅AB eAC≅AD e l'angolo β congruente. Quest'ultimo però non è compreso tra i due lati. Quindi, la presenza di due lati congruenti e di un angolo non compreso tra di essi non è sufficiente a dichiarare la congruenza dei triangoli.
Il primo criterio di congruenza è da considerarsi un postulato.
Il secondo criterio di congruenza dei triangoli
Due triangoli sono congruenti se hanno congruenti nello stesso ordine due angoli e il lato adiacente tra di essi.
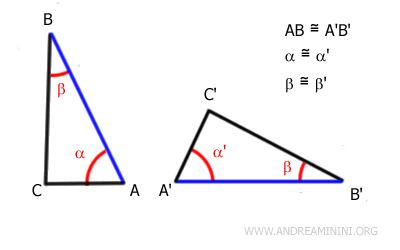
In altre parole, i triangoli sono congruenti quando hanno due angoli della stessa ampiezza e il lato adiacente tra i due angoli della stessa lunghezza.
E' anche conosciuto come criterio ALA (Angolo-Lato-Angolo)
In questo caso si tratta di un teorema perché è dimostrabile.
Secondo il V postulato di Euclide la somma degli angoli interni di un triangolo è sempre uguale a un angolo piatto (180°). Pertanto, se si conoscono due angoli, è conosciuta l'ampiezza anche del terzo angolo per differenza.
Il secondo criterio di congruenza ha anche una forma generalizzata detta "secondo criterio generalizzato" o "quarto criterio di congruenza" dei triangoli.
Due triangoli sono congruenti se hanno due angoli e un lato congruenti nello stesso ordine, con il lato non necessariamente compreso tra i due angoli.
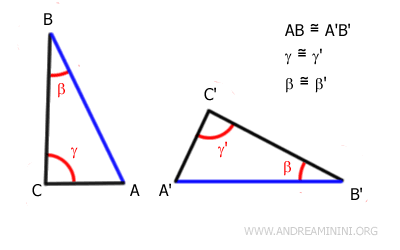
In questo caso il lato congruente può essere uno qualsiasi, non occorre che sia il lato compreso tra gli angoli.
Il terzo criterio di congruenza dei triangoli
Due triangoli sono congruenti se hanno tutti i lati congruenti.
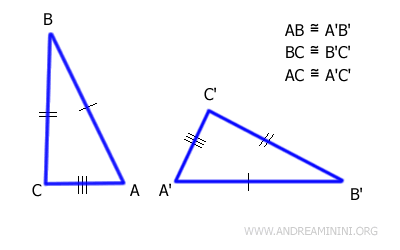
In pratica, i triangoli sono congruenti se hanno i lati della stessa lunghezza.
E' anche conosciuto come criterio LLL (Lato-Lato-Lato)
Anche in questo caso su tratta di un teorema perché è dimostrabile.
Nota. La congruenza di tutti gli angoli AAA, invece, è una condizione necessaria ma non sufficiente per la congruenza dei triangoli. Due triangoli potrebbero avere gli angoli congruenti ma lati di lunghezza diversa. In questo caso i due triangoli non sono congruenti perché non sono sovrapponibili. I due triangoli hanno la stessa forma ma uno è più grande dell'altro. Viceversa, due triangoli con i lati congruenti (LLL) hanno sempre gli angoli congruenti. Pertanto, il criterio AAA non è un criterio di congruenza dei triangoli.
E così via.
