Calcolo area del triangolo con la trigonometria
L'area del triangolo è uguale al semi prodotto di due lati l1, l2 per il seno dell'angolo (α) compreso tra i due lati. $$ Area = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$
Dove l1 e l2 sono due lati adiacenti del triangolo mentre α è l'angolo compreso tra i due lati.
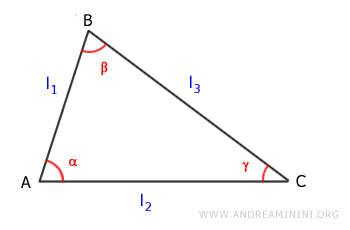
Allo stesso modo sono valide anche le formule
$$ Area = \frac{1}{2} \cdot (l_1 \cdot l_3) \cdot \sin \beta $$
$$ Area = \frac{1}{2} \cdot (l_2 \cdot l_3) \cdot \sin \gamma $$
Le formule sono applicabili a qualsiasi tipo di rettangolo (isoscele, rettangolo, scaleno).
Un esempio pratico
Prendo in considerazione un triangolo rettangolo
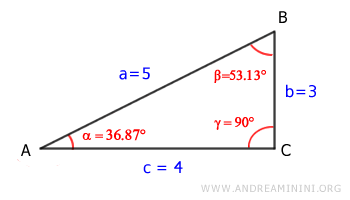
L'area del triangolo è base (c) per altezza (b) diviso due.
$$ Area = \frac{1}{2} (c \cdot b ) = \frac{1}{2} (4 \cdot 3 ) = 6 $$
Provo a calcolare l'area usando la trigonometria.
Prendo in considerazione i lati adiacenti a=5, c=4 e l'angolo alfa α=36,87° compreso tra di essi.
$$ Area = \frac{1}{2} (a \cdot c ) \sin \alpha $$
$$ Area = \frac{1}{2} (5 \cdot 4 ) \sin 36,87° $$
$$ Area = \frac{1}{2} (20 ) \cdot 0,6 $$
$$ Area = 6 $$
Il risultato è sempre lo stesso.
Inoltre, se considero i lati adiacenti a=5, b=3 e l'angolo beta β=53,13° tra di essi, giungo allo stesso risultato.
$$ Area = \frac{1}{2} (a \cdot b ) \sin \beta $$
$$ Area = \frac{1}{2} (5 \cdot 3 ) \sin 53,13° $$
$$ Area = \frac{1}{2} (15 ) \cdot 0.8 $$
$$ Area = 6 $$
Allo stesso modo, se considero i lati adiacenti c=4, b=3 e l'angolo gamma γ=90° tra di essi, il risultato è sempre lo stesso.
$$ Area = \frac{1}{2} (c \cdot b ) \sin \gamma $$
$$ Area = \frac{1}{2} (4 \cdot 3 ) \sin 90° $$
$$ Area = \frac{1}{2} (12) \cdot 1 $$
$$ Area = 6 $$
In ogni caso l'area del triangolo è 6.
Esempio 2
In questo esempio considero un triangolo isoscele
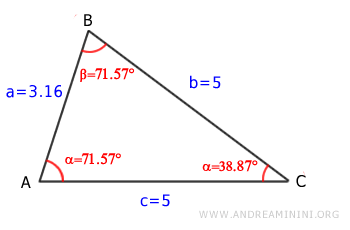
Calcolo l'area usando i lati b=5 e c=5 e l'angolo compreso γ=36,87°
$$ Area = \frac{1}{2} (b \cdot c ) \sin \gamma $$
$$ Area = \frac{1}{2} (5 \cdot 5 ) \sin 36,87° $$
$$ Area = \frac{1}{2} (25 ) \cdot 0,6 $$
$$ Area = 7,5 $$
In alternativa, calcolo l'area usando i lati a=3,16 e c=5 e l'angolo compreso α=71,57°
$$ Area = \frac{1}{2} (a \cdot c ) \sin \alpha $$
$$ Area = \frac{1}{2} (3,16 \cdot 5 ) \sin 71,57° $$
$$ Area = 7,5 $$
oppure i lati a=3,16 e b=5 el'angolo compreso β=71,57°
$$ Area = \frac{1}{2} (3,16 \cdot 5 ) \sin 71,57° $$
$$ Area = 7,5 $$
In ogni caso il risultato è sempre lo stesso.
L'area del triangolo è 7,5.
La dimostrazione
Caso 1
Prendo in considerazione un triangolo rettangolo
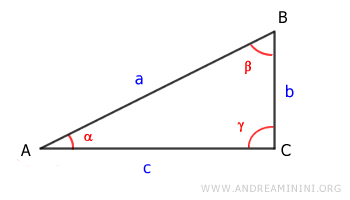
L'area di un triangolo è base (c) per altezza (b) diviso due.
$$ Area = \frac{1}{2} \cdot c \cdot b $$
Secondo il primo teorema del triangolo rettangolo la lunghezza del cateto b (altezza) è uguale all'ipotenusa (a) per seno dell'angolo opposto (alfa) ossia b=a sin α
$$ Area = \frac{1}{2} \cdot c \cdot (a \cdot \sin \alpha) $$
$$ Area = \frac{1}{2} \cdot ( c \cdot a ) \cdot \sin \alpha $$
Dove l'angolo alfa è l'angolo compreso tra i lati a e c del triangolo.
In questo modo ottengo la formula che volevo dimostrare.
Caso 2
Prendo in considerazione un triangolo isoscele con i lati b = c e gli angoli α = β congruenti
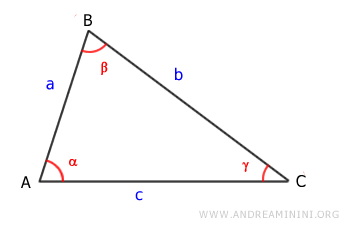
Traccio l'altezza (h) del triangolo. E' il segmento BD.
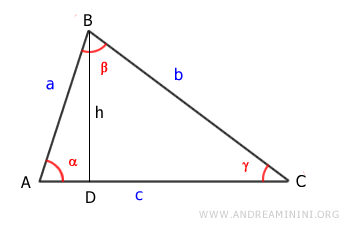
L'area del triangolo è la base (c) per l'altezza (h) diviso due.
$$ Area = \frac{1}{2} \cdot c \cdot h $$
L'altezza (h) è il cateto del triangolo rettangolo ABD.
Secondo il primo teorema del triangolo rettangolo la lunghezza del segmento BD (l'altezza h) è uguale all'ipotenusa (AB) per il seno dell'angolo opposto (α) ossia h = a · sin(α)
$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin \alpha $$
Dove l'angolo acuto alfa è l'angolo compreso tra i lati a e c del triangolo isoscele.
E ottengo di nuovo la formula che volevo dimostrare.
Caso 3
Prendo in considerazione un triangolo scaleno con un angolo ottuso (α)
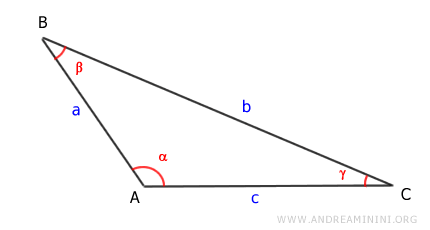
Traccio l'altezza (h) del triangolo. E' il segmento AD.
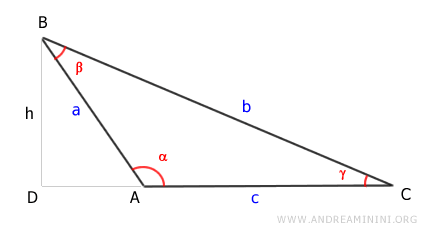
L'area del triangolo è la base (c) per l'altezza (h) diviso due.
$$ Area = \frac{1}{2} \cdot c \cdot h $$
L'altezza h è il lato AD del triangolo rettangolo ADB
Secondo il primo teorema del triangolo rettangolo la lunghezza del segmento BD (l'altezza h) è uguale all'ipotenusa (AB) per il seno dell'angolo opposto (π-α) ossia h = a · sin(π-α)
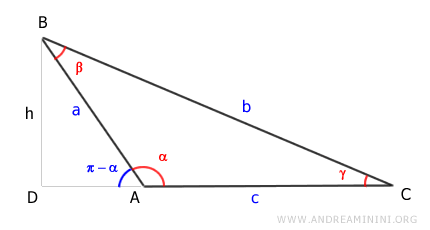
Sostituisco h con a · sin(π-α)
$$ Area = \frac{1}{2} \cdot c \cdot h $$
$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin ( \pi - \alpha ) $$
L'angolo opposto (π-α) è l'angolo supplementare dell'angolo ottuso α.
Sapendo che per la proprietà degli angoli associati vale l'uguaglianza sin(π-α) = sin(α) posso riscrivere la formula in questa forma equivalente
$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin ( \alpha ) $$
Dove l'angolo ottuso α è l'angolo compreso tra i lati a e c del triangolo scaleno.
Così facendo ottengo nuovamente la formula che volevo dimostrare.
In conclusione, la formula per calcolare l'area è valida per qualsiasi tipo di triangolo.
E così via
