Il teorema delle disuguaglianze triangolari

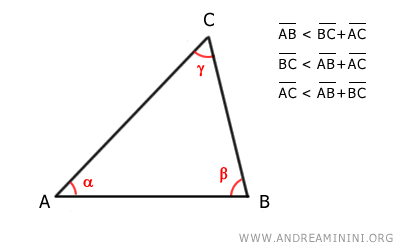
In un triangolo ciascun lato è minore della somma degli altri due lati.

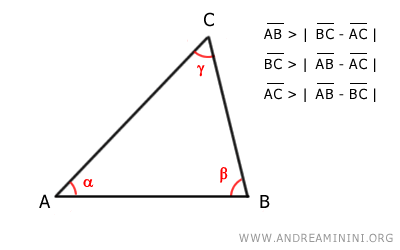
Inoltre ciascun lato è maggiore della differenza degli altri due lati.

Ad esempio, dato il triangolo ABC.

Il lato AB è minore della somma dei lati BC+AC.

$$ \overline{AB} < \overline{BC}+\overline{AC} $$

Lo stesso vale per gli altri due lati

$$ \overline{BC} < \overline{AB}+\overline{AC} $$

$$ \overline{AC} < \overline{AB}+\overline{BC} $$

Un esempio pratico

Considero un triangolo ABC

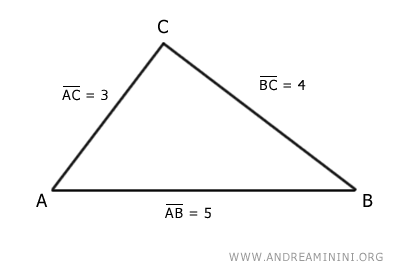
I lati del triangolo hanno queste misure

$$ \overline{AB} = 5 $$

$$ \overline{BC} = 4 $$

$$ \overline{AC} = 3 $$

Il lato AB di lunghezza pari a 5 è minore della somma degli altri due AC+BC

$$ 5 < 4 + 3 = 7 $$

Il lato AB è maggiore della differenza degli altri due lati AC-BC

$$ 5 > 4 - 3 = 1 $$

Il lato BC di lunghezza pari a 4 è minore della somma degli altri due AB+AC

$$ 4 < 5 + 3 = 8 $$

Il lato BC è maggiore della differenza degli altri due lati AB-AC

$$ 4 > 5 - 3 = 2 $$

Il lato AC di lunghezza pari a 3 è minore della somma degli altri due AB+BC

$$ 3 < 5 + 4 = 9 $$

Il lato AC è maggiore della differenza degli altri due lati AB-BC

$$ 3 > 5 - 4 = 1 $$

Tutte le relazioni della disuguaglianza triangolare sono soddisfatte.

La dimostrazione

Prendo in considerazione un triangolo ABC in cui il lato maggiore è AC.

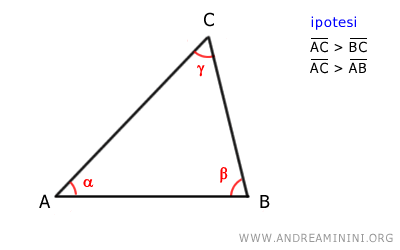
Le ipotesi iniziali sono le seguenti:

$$ \overline{AC} > \overline{BC} $$

$$ \overline{AC} > \overline{AB} $$

Devo dimostrare che il lato AC è minore della somma degli altri due.

$$ \overline{AC} < \overline{BC} + \overline{AB} $$

Inoltre, devo dimostrare che il lato BC è maggiore della differenza degli altri due.

$$ \overline{AC} - \overline{AB} < \overline{BC} $$

Prolungo il lato AB con un segmento BD congruente con BC.

 

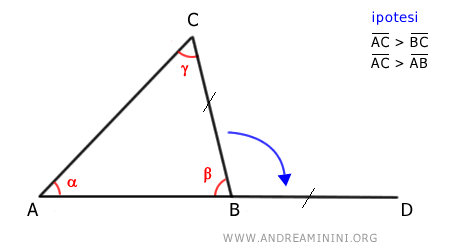
Poi traccio un segmento CD che congiuge i punti C e D.

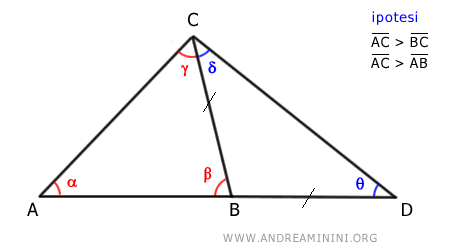
Il triangolo BDC è un triangolo isoscele perché ha due lati congruenti (BD≅BC) per costruzione.

Quindi, essendo un triangolo isoscele, gli angoli alla base sono tra loro congruenti (δ≅θ).

$$ \delta \cong θ $$

E subito evidente che l'angolo γ + δ è maggiore di δ

$$ \gamma + \delta > \delta $$

Sapendo che gli angoli δ≅θ sono congruenti, deduco che l'angolo γ + δ è anche maggiore di θ

$$ \gamma + \delta > θ $$

Ora considero il triangolo ADC

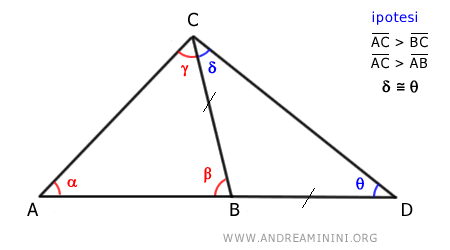
Secondo il teorema dell'angolo maggiore, nel triangolo ADC il lato AC opposto all'angolo θ è minore del lato AD opposto all'angolo γ + δ

$$ \overline{AC} < \overline{AD} $$

Sapendo che il lato AD è la somma dei segmenti AB+BD

$$ \overline{AC} < \overline{AB} + \overline{BD} $$

Inoltre, sapendo che i lati BC e BD sono congruenti (BC≅BD)

$$ \overline{AC} < \overline{AB} + \overline{BC} $$

Ho così dimostrato che il lato AC è minore della somma dei lati AB e BC del triangolo ABC.

A questo punto, applico la proprietà invariantiva e sottraggo a entrambi i membri della diseguaglianza il lato AB

$$ \overline{AC} - \overline{AB} < \overline{AB} + \overline{BC} - \overline{AB} $$

$$ \overline{AC} - \overline{AB} < \overline{BC} $$

In questo modo ho anche dimostrato che il lato BC è maggiore della differenza degli altri due lati del triangolo ABC.

La distanza tra tre punti nello spazio

In generale, il teorema della disuguaglianza triangolare è alla base di un altro teorema della distanza.

In uno spazio metrico dati tre punti qualsiasi dello spazio A, B e C, la distanza tra due punti d(A,B) è minore o uguale della somma delle distanze tra gli altri due punti d(B,C)+d(A,C). $$ d(A,B) \le d(B,C) + d(A,C) $$

In questo caso devo considerare anche il caso dell'uguaglianza che si verifica quando i punti A,B e C sono coincidenti.

Osservazioni

Alcune osservazioni sul teorema delle disuguaglianze triangolari

• Dati tre segmenti a,b,c la costruzione di un triangolo con i tre segmenti è possibile solo se ciascun segmento è minore della somma degli altri due segmenti. $$ a < b+c $$ $$ b < a+c $$ $$ c < a+b $$

E così via.