Teorema della bisettrice di un angolo interno di un triangolo
La bisettrice di un angolo interno di un triangolo divide il lato opposto in due parti direttamente proporzionali agli altri due lati del triangolo. $$ \overline{BD} : \overline{CD} = \overline{AB} : \overline{AC} $$ 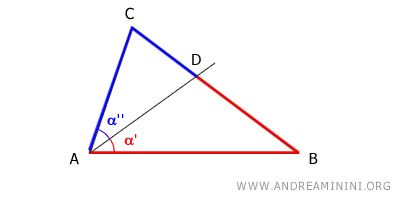
In altre parole, se ho un triangolo ABC con una bisettrice che parte da un angolo A e interseca il lato opposto BC in un punto D, allora la lunghezza del segmento BD è proporzionale alla lunghezza del segmento CD, e questa proporzione è uguale alla proporzione delle lunghezze dei lati adiacenti al triangolo, cioè AB/AC.
Matematicamente, posso esprimerlo con la seguente proporzione:
$$ \overline{AB}:\overline{AC} = \overline{BD}:\overline{CD} $$
che può essere scritta anche in forma frazionaria
$$ \frac{ \overline{AB} }{ \overline{AC} } = \frac{ \overline{BD} }{ \overline{CD} } $$
Questo teorema è utile in molte applicazioni geometriche e posso utilizzarlo per risolvere problemi relativi ai triangoli quando conosco alcune delle loro lunghezze o angoli.
Vale anche il teorema inverso. Se un punto divide un lato del triangolo in due segmenti proporzionali agli altri due lati del triangolo, allora il segmento che congiunge il punto con il vertice opposto del triangolo è la bisettrice del suo angolo.
Un esempio pratico
Prendo come esempio un triangolo con i lati di lunghezza predefinita AB=4, BC=5, AC=3.
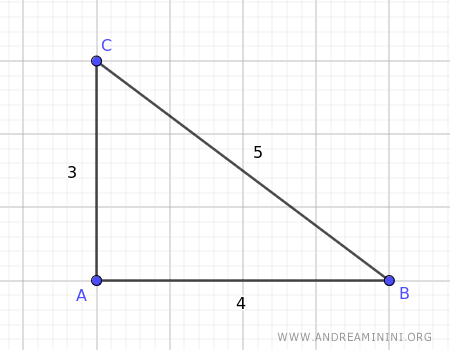
Traccio la bisettrice dell'angolo al vertice A.
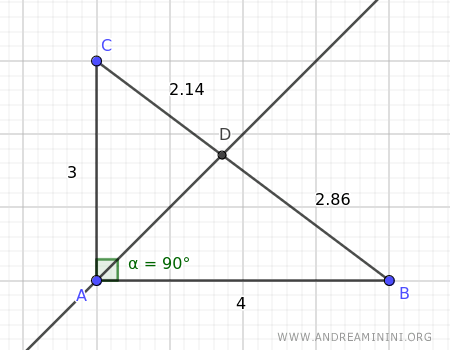
La bisettrice dell'angolo $ \hat{A} $ taglia il lato opposto del triangolo $ \overline{BC} $ in due segmenti BD=2.86 e CD=2.14.
Il rapporto tra i segmenti BD e CD è circa 1.34
$$ \frac{ \overline{BD} }{ \overline{CD} } = \frac{ 2.86 }{ 2.14 } = 1.33 $$
A questo punto verifico se questi due segmenti sono proporzionali agli altri due lati AB e AC del triangolo.
$$ \frac{ \overline{AB} }{ \overline{AC} } = \frac{ 4 }{ 3 } = 1.33 $$
Il rapporto è lo stesso, quindi i segmenti BD e CD sono direttamente proporzionali ai lati AB e AC del triangolo ABC.
La dimostrazione
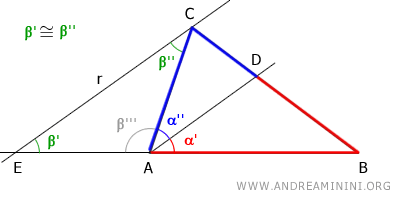
Considero un triangolo ABC qualsiasi.
Traccio la bisettrice dell'angolo $ \hat{A} $ che interseca il lato opposto BC nel punto D, dividendolo in due segmenti BD e CD.
La bisettrice divide l'angolo al vertice A in due angoli di pari ampiezza α'≅α'' (congruenti).
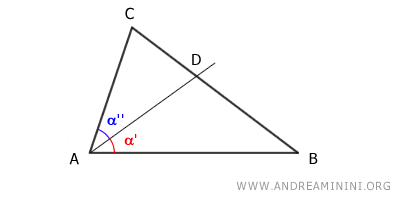
Devo dimostrare che il segmento BD sta a CD come AB sta a AC
$$ BD : CD = AB : AC $$
In altre parole devo dimostre che BD e CD sono direttamente proporzionali ad AB e AC.
Traccio la retta r parallela alla bisettrice che passa per il vertice C.
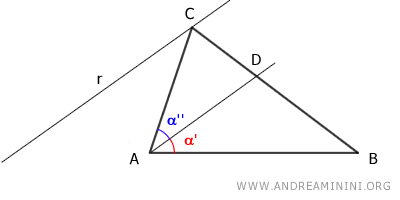
Poi prolungo la il lato BA fino all'intersezione con la retta r nel punto E.
Si forma così un triangolo EAC con gli angoli β', β'', β''' e un triangolo più grande EBC.
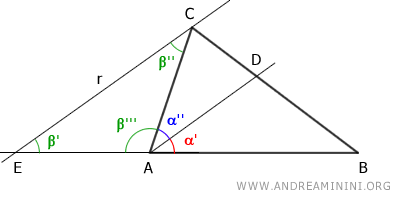
La retta AD è parallela al lato EC del triangolo EBC, quindi divide gli altri due lati del triangolo EBC in segmenti proporzionali secondo il teorema della retta parallela al lato di un triangolo.
$$ BD:CD = AB:AE $$
Gli angoli α'' e β'' sono angoli alterni interni di due rette parallele tagliate da una trasversale AC, quindi per il teorema delle rette parallele sono angoli congruenti α''≡β''
$$ \alpha '' \cong \beta '' $$
Gli angoli α' e β' sono angoli corrispondenti di due rette parallele tagliate da una trasversale AC, quindi sempre per il teorema delle rette parallele sono angoli congruenti α'≡β'
$$ \alpha ' \cong \beta ' $$
Sapendo che la bisettrice AC del triangolo ABC divide l'angolo al vertice A in due angoli congruenti α'≅α'', deduco per la triangolarità che anche β'≅β'' sono congruenti.
$$ \beta ' \cong \beta '' $$
Pertanto il triangolo EAC è un triangolo isoscele sulla base EC, perché ha due angoli congruenti β'≅β''.
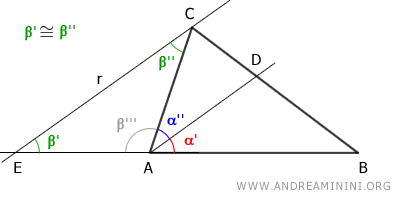
Sapendo che EAC è un triangolo isoscele, deduco che ha i lati obliqui congruenti EA≅AC.
$$ \overline{EA} \cong \overline{AC} $$
A questo punto torno alla proporzione del triangolo EAC
$$ BD:CD = AB:AE $$
Poiché EA≅AC sostituisco AE con AC
$$ BD : CD = AB : AC $$
E questo dimostra la proporzione iniziale.
Quindi i segmenti BD e CD ottenuti tagliando il lato BC con la bisettrice dell'angolo al vertice A, sono direttamente proporzionali agli altri lati AB e AC del triangolo ABC.
Nota. Poiché il teorema della retta parallela al lato di un triangolo deriva dal teorema di Talete, deduco che anche questo teorema della bisettrice è un corollario del teorema di Talete.
E così via.
