Il secondo criterio di congruenza dei triangoli
Due triangoli sono congruenti se due angoli corrispondenti sono congruenti e il lato adiacente a questi angoli è anch'esso congruente nei due triangoli.
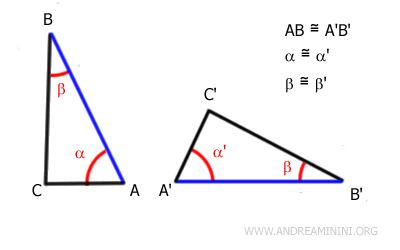
In altri termini, i triangoli sono congruenti quando presentano due angoli di uguale misura e il lato compreso tra questi due angoli ha la stessa lunghezza negli entrambi i triangoli.
Questo criterio è anche noto come ALA (Angolo-Lato-Angolo)
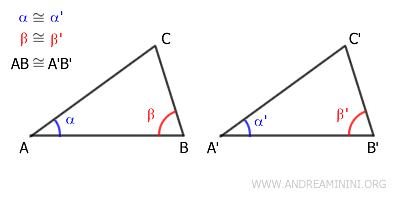
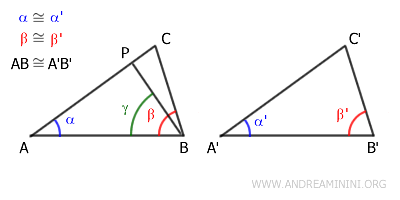
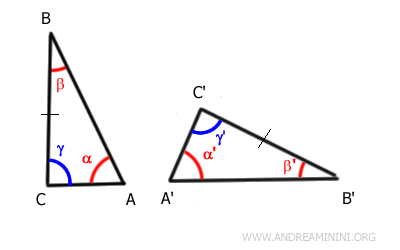
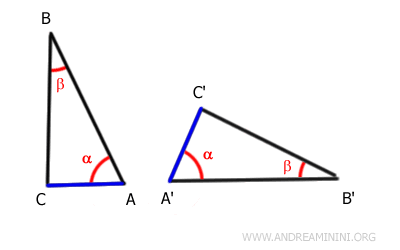
Ad esempio, considero questi due triangoli ABC e A'B'C'.
Gli angoli α≅α' e β≅β' sono congruenti tra loro ossia hanno la stessa ampiezza.
Anche i lati adiacenti agli angoli AB≅A'B' sono congruenti, ossia hanno la stessa lunghezza.

Da questo deduco che anche gli altri lati e angoli sono congruenti.
Pertanto, i due triangoli sono congruenti tra loro. In altre parole, secondo la definizione di congruenza, sono sovrapponibili punto a punto dopo un movimento rigido.
La dimostrazione
Il secondo criterio di congruenza è un teorema perché è dimostrabile.
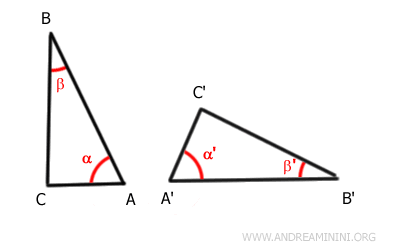
Prendo come esempio due triangoli ABC e A'B'C'

Per ipotesi gli angoli α≅α' e β≅β' sono congruenti e il lato adiacente agli angoli AB≅A'B' è congruente.
Se i lati AB≅A'B' sono congruenti, allora sono sovrapponibili.
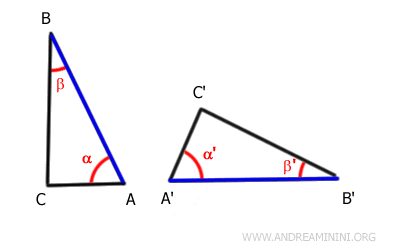
Questo vuol dire che anche gli estremi dei segmenti AB e A'B' sono sovrapponibili.
In altre parole, i punti A e A' e i punti B e B' sono coincidenti.
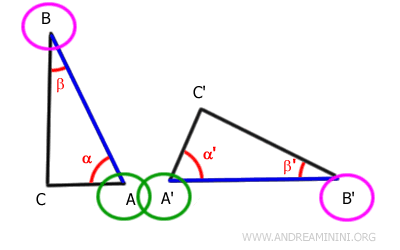
Essendo congruenti anche gli angoli α≅α', anche le semirette che contengono i lati AC e A'C' sono sovrapponibili.
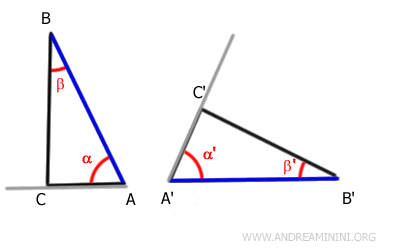
In modo analogo, essendo congruenti gli angoli β≅β', anche le semirette che contengono i lati BC e B'C' sono sovrapponibili.
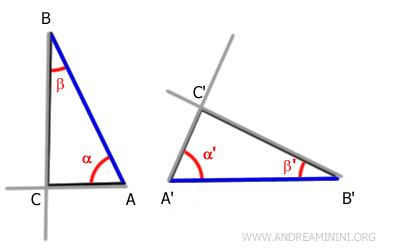
Pertanto, le semirette si intersecano nello stesso punto.
Questo vuol dire che anche i punti C è C' sono sovrapponibili.
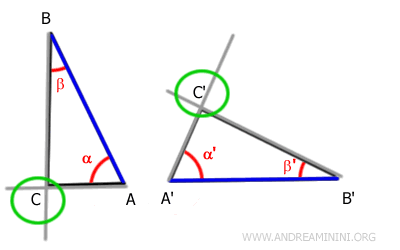
In conclusione, tutti i vertici dei due triangoli sono ordinatamente sovrapponibili.
Questo significa che tutti i lati sono congruenti AB≅A'B' , BC≅B'C' , AC≅A'C'.
Di conseguenza anche tutti gli angoli compresi tra i lati sono congruenti.
Quindi, i due triangoli sono congruenti.
Dimostrazione alternativa
In questo caso seguo una dimostrazione per assurdo.
Considero due triangoli ABC e A'B'C' che hanno due angoli congruenti \( \alpha \cong \alpha' \) e \( \beta \cong \beta' \) e un lato \( AB \cong A'B' \) congruente.
Per assurdo, ipotizzo che due triangoli non siano congruenti (tesi).
$$ ABC \not \cong A'B'C' $$
Non essendo congruenti, il lato AC può essere maggiore o minore del lato A'C'
Se il lato è maggiore $ AC > A'C' $, allora posso trovare un punto P all'interno del lato AC tale che $ AP \cong A'B' $
I due triangoli ABP e A'B'C hanno un angolo congruente per ipotesi \( \alpha \cong \alpha' \), un lato congruente per ipotesi \( AB \cong A'B' \) e un lato congruente \( AP \cong A'C' \) per costruzione.
Per il primo criterio di congruenza i due triangoli ABP e A'B'C' sono congruenti, quindi hanno tutti gli angoli e i lati congruenti nello stesso ordine.
$$ ABP \cong A'B'C' $$
In particolar modo, mi interessa sapere che gli angoli corrispondenti \( \gamma \cong \beta' \) dovrebbero essere congruenti.

Tuttavia, per ipotesi iniziale gli angoli \( \beta \cong \beta' \) sono congruenti. Questo significa che, per la proprietà transitiva, anche gli angoli \( \gamma \cong \beta \) sono congruenti.
$$ \gamma \cong \beta' \cong \beta' $$
Questo però è assurdo perché il punto \( P \) è un punto interno del segmento \( AC \), quindi l'angolo \( \gamma \) dovrebbe essere minore dell'angolo \( \beta \).
Si giunge così a una contraddizione e devo concludere che la tesi "i due triangoli non sono congruenti" è falsa.
Di conseguenza è vera la tesi contraria, ossia i due triangoli sono congruenti.
Nota. Allo stesso risultato posso giungere considerando AC<A'C'. Quindi, i lati AC e A'C' devono necessariamente essere congruenti.
Il secondo criterio di congruenza generalizzato
Il secondo criterio di congruenza dei triangoli possiede anche una forma estesa, conosciuta come 'secondo criterio generalizzato' o 'quarto criterio di congruenza'.
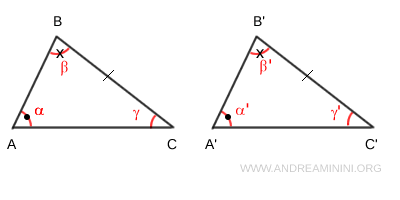
Due triangoli sono congruenti se possiedono due angoli congruenti e un lato congruente, anche se il lato non è necessariamente compreso tra i due angoli.
In questo caso il lato congruente del triangolo può essere uno qualsiasi, può anche non essere il lato compreso tra i due angoli.
Per dirla diversamente, gli angoli congruenti possono anche non essere adiacenti al lato congruente dei triangoli.
E' però importante che gli angoli e il lato siano ordinatamente congruenti ossia nello stesso ordine in entrambi i triangoli.
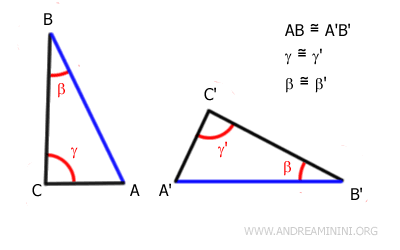
Esempio. Questi due triangoli hanno gli angoli $ \alpha \cong \alpha' $ e $ \beta \cong \beta' $ congruenti e il lato $ BC \cong BC' $ congruente. Gli angoli e il lato sono congruenti nello stesso ordine. Quindi, applico il secondo teorema generalizzato di congruenza e affermo che i trangoli $ ABC \cong A'B'C' $ sono congruenti.
Fin qui tutto chiaro... Ora prendo il triangolo ABC e con un compasso centrato in A traccio un arco con apertura AB individuando il punto C' sul segmento AC. Poi traccio un segmento B'C' parallelo a BC. In questo modo ottengo un secondo triangolo AB'C'. Per costruzione anche questi due triangoli hanno due angoli congruenti $ \alpha $ e $ \beta \cong \beta' $ e un lato congruente $ AB \cong B'C' $ ma non sono triangoli congruenti $ ABC \not \cong AB'C' $ perché il lato e gli angoli non sono congruenti nello stesso ordine.
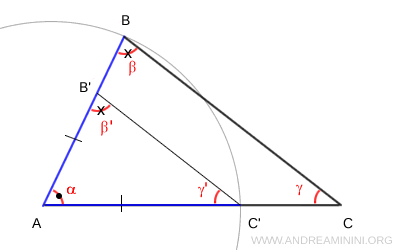
Questo dimostra che, per applicare il secondo teorema generalizzato di congruenza, è molto importante che gli angoli e il lato siano "ordinatamente congruenti".
Dimostrazione
Secondo il teorema della somma degli angoli interni di un triangolo, la somma degli angoli interni di un triangolo è congruente a un angolo piatto (180°)
$$ \alpha + \beta + \gamma = 180° $$
Quindi, se in due triangoli ABC e A'B'C' sono congruenti due angoli α≅α' e β≅β' anche il terzo angolo è congruente γ≅γ' per differenza

L'angolo gamma restante in entrambi i triangoli posso ricavarlo per differenza.
$$ \gamma = 180° - \alpha -\beta $$
$$ \gamma' = 180° - \alpha' -\beta' $$
Sapendo che α≅α' e β≅β' deduco che anche l'angolo γ≅γ' è congruente
$$ \gamma \cong \gamma' $$
Ora, per ipotesi, considero che i due triangoli ABC e A'B'C' abbiano anche un lato congruente $ BC \cong B'C' $ nello stesso ordine.
In questo caso, sapendo che anche gli angoli $ gamma \cong \gamma' $ sono congruenti, posso affermare che i triangoli $ ABC \cong A'B'C' $ sono congruenti per il secondo criterio di congruenza, perché hanno un lato congruente $ BC \cong B'C' $ e gli angoli adiacenti congruenti $ \gamma \cong \gamma' $ e $ \beta \cong \beta' $ nello stesso ordine.
Pertanto, due triangoli sono congruenti se hanno due angoli e un lato congruente nello stesso ordine, anche se il lato non è adiacente agli angoli.
Dimostrazione alternativa
ll secondo criterio di congruenza dei triangoli si può dimostrare per assurdo.
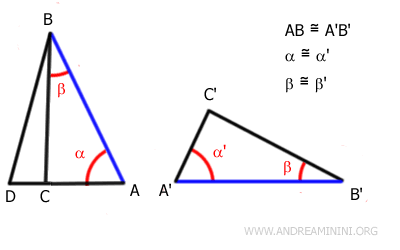
Considero due triangoli ABC e A'B'C'

Per ipotesi gli angoli α≅α' e β≅β' sono congruenti e il lato adiacente agli angoli AB≅A'B' è congruente.
Pertanto, per il secondo criterio di congruenza i due triangoli sono congruenti.
Per assurdo, cerco di dimostrare la tesi per la quale i lati non adiacenti agli angoli AC e A'C' non sono congruenti ossia AC≠A'C' hanno una lunghezza differente.
Per il postulato del trasporto dei segmenti, questo vuol dire che esiste un estremo D su AC tale che AD=A'C'
Traccio il segmento DB e considero il triangolo ADB.
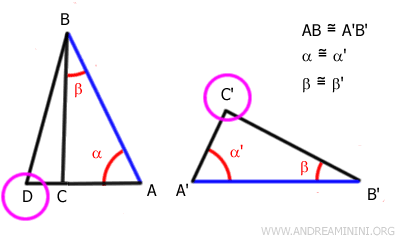
Per il primo criterio di congruenza i due triangoli ABD e A'B'C' sono congruenti.
Perché? Se il lato AD≅A'C' è congruente, dall'ipotesi iniziale so già che anche il lato AB≅A'B' è congruente e l'angolo α≅α' tra di essi congruente. Quindi, due lati e l'angolo tra di essi sono congruenti. Per il primo principio di congruenza i due triangoli ABD e A'B'C' sono congruenti.
Se i due triangoli ABD e A'B'C' sono congruenti, allora anche l'angolo nei vertici D=C' è congruente.
Tuttavia, per l'ipotesi inziale l'angolo nei vertici C'=C è congruente perché sono congruenti i due restanti angoli α≅α' e β≅β'.
Secondo il V postulato di Euclide, la somma degli angoli interni di un triangolo è sempre uguale a un angolo piatto (180°) nella geometria euclidea. $$ \alpha + \beta + \gamma = 180° $$ Pertanto, se si conoscono due angoli, non importa quali siano, è conosciuta l'ampiezza anche del terzo angolo per differenza. Quindi se due angoli hanno la stessa ampiezza α≅α' e β≅β', anche l'ampiezza del terzo angolo è la stessa $$ 180°-α-β≅180°-α'-β' $$
Quindi, per proprietà transitiva l'angolo nel vertice D è congruente all'angolo nel vertice C.
Pertanto i lati AD e AC devono essere congruenti AD≅AC.
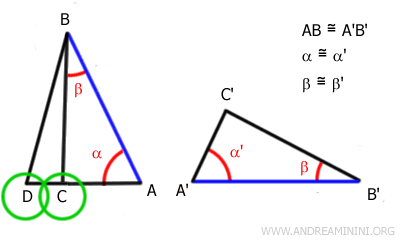
Sapendo che AD≅A'C', se AD≅AC allora anche AC≅A'C'
$$ \overline{AC} \cong \overline{AD} \cong \overline{A'C'} $$
Questo vuol dire che i lati AC e A'C' non possono avere una lunghezza diversa. La tesi AC≠A'C' è falsa.
Di conseguenza è vera l'ipotesi contraria alla tesi AC≅A'C' ossia i lati AC e A'C' sono congruenti.
Quindi, per stabilire la congruenza di due triangoli è sufficiente che due angoli e un lato qualsiasi siano congruenti.
E così via.
