L'altezza di un triangolo
L'altezza (h) di un triangolo è un segmento perpendicolare che congiunge un vertice con il lato opposto o il suo prolungamento.
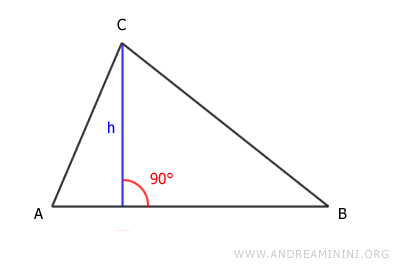
In altri termini, è la distanza perpendicolare dal vertice al lato opposto scelto come base.
L'altezza forma due angoli retti sulla base.
Poiché il triangolo ha tre lati e qualsiasi lato può essere scelto come base, deduco che il triangolo ha sempre tre altezze.
Ad esempio, se scelgo il lato CB come base l'altezza è la seguente
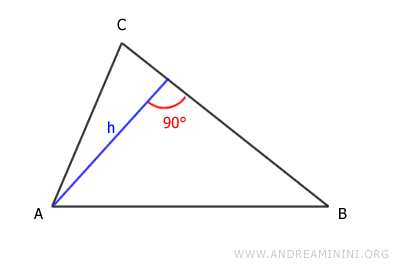
Infine, se scelgo come base il lato AC l'altezza è la seguente:
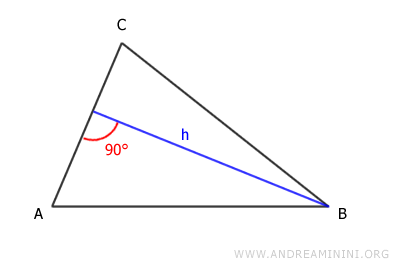
L'altezza (h) può essere anche un segmento esterno al triangolo perché in alcuni casi è perpendicolare a un prolungamento della base.
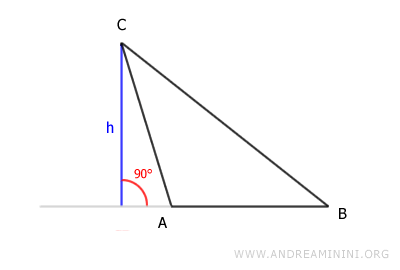
Questo aspetto distingue l'altezza dalla bisettrice e dalla mediana che, invece, sono sempre segmenti interni al triangolo.
Come si calcola l'altezza di un triangolo
La formula per ottenere l'altezza di un triangolo è la seguente
$$ h = \frac{2A}{b} $$
Dove A è l'area del triangolo e b la lunghezza della base.
Quindi, per calcolare l'altezza del triangolo, basta dividere il doppio dell'area per la lunghezza della base.
Nota. Questa formula si ottiene sapendo che l'area (A) del triangolo è uguale alla base per l'altezza diviso due. $$ A = \frac{b \cdot h}{2} $$ Riorganizzando la formula per trovare h (l'altezza). Moltiplico per due entrambi i membri. $$ 2 \cdot A = 2 \cdot \frac{b \cdot h}{2} $$ $$ 2 \cdot A = b \cdot h $$ Divido per la base entrambi i membri e semplifico $$ \frac{1}{b} \cdot 2 \cdot A = \frac{1}{b} \cdot b \cdot h $$ $$ \frac{2A}{b} = h $$
Un esempio pratico
Considero un triangolo ABC
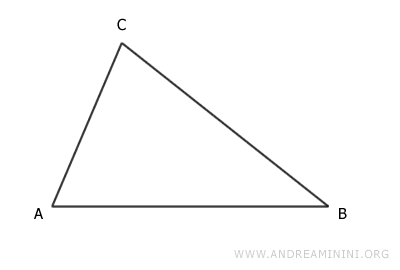
Considero come base il segmento AB
Quindi, traccio un segmento perpendicolare alla base AB che passa per il vertice opposto C.

Questo segmento è l'altezza del triangolo.
Come trovare l'altezza del triangolo. Dal punto di vista geometrico, per trovare l'altezza rispetto alla base AB punto il compasso sul vertice opposto C e con raggio AC traccio un arco che individua il punto D.
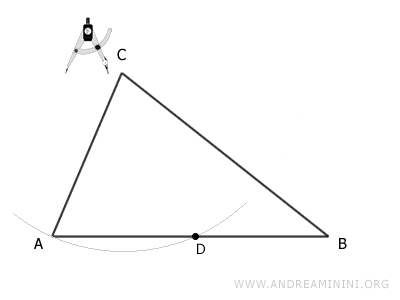
Mantenendo la stessa apertura del compasso traccio un arco con centro A e un altro arco con centro D. L'intersezione tra questi due archi individua un punto E esterno al triangolo.
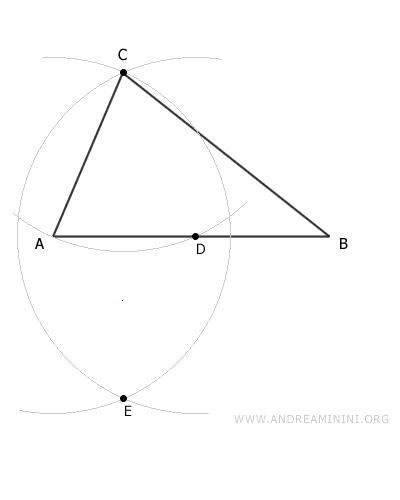
Traccio un segmento EC che individua sulla base il punto F. Il segmento EC è perpendicolare alla base ossia forma un angolo di 90°- L'altezza del triangolo è il segmento CF. Per vedere tutti i passaggi in modo dettagliato clicca qui.
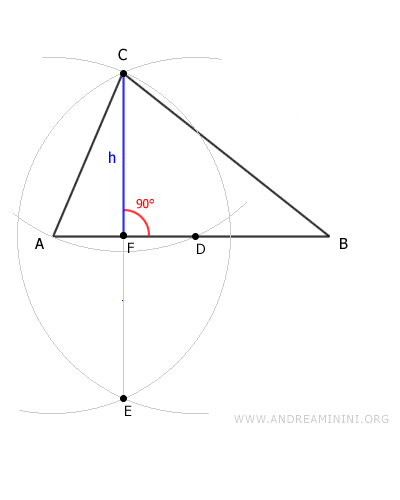
Altezza di un triangolo equilatero
L'altezza di un triangolo equilatero può essere calcolata usando la seguente formula: \[ h = \frac{\sqrt{3}}{2} \cdot l \] dove \( h \) è l'altezza e \( l \) è la lunghezza del lato del triangolo equilatero.
La formula per calcolare l'altezza di un triangolo equilatero deriva dalle proprietà geometriche di questo tipo di triangolo.
In questo caso basta conoscere la misura di un lato per determinare l'altezza del triangolo.
Esempio
Un triangolo equilatero ABC ha tutti i lati di lunghezza 6.
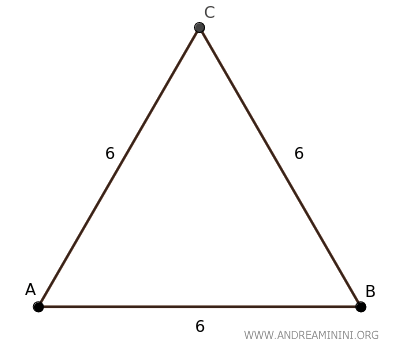
Per conoscere l'altezza del triangolo equilatero applico la formula:
$$ h = \frac{\sqrt{3}}{2} \cdot l $$
In questo caso $ l = 6 $
$$ h = \frac{\sqrt{3}}{2} \cdot 6 $$
$$ h = 3 \cdot \sqrt{3} $$
$$ h \approx 5.1962 $$
Quindi, l'altezza del triangolo equilatero è approssimativamente 5.1962
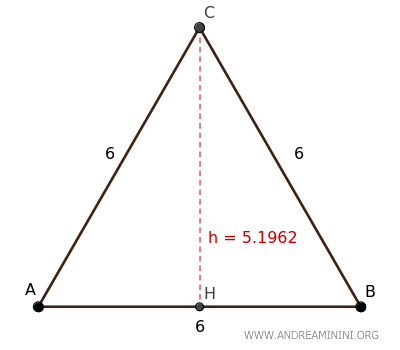
Dimostrazione
Un triangolo equilatero ha tutti e tre i lati di uguale lunghezza.
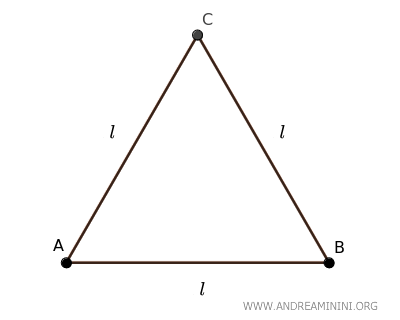
Se traccio un'altezza da uno dei vertici al lato opposto, divido il triangolo equilatero in due triangoli rettangoli congruenti $ ACH \cong BCH $.
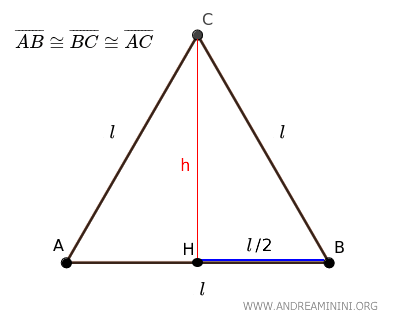
In ogni triangolo rettangolo, l'altezza \( h \) è uno dei cateti, la metà della base \( l/2 \) è l'altro cateto, e il lato del triangolo equilatero \( l \) è l'ipotenusa.
Per conoscere la lunghezza del cateto del triangolo rettangolo, posso applicare il teorema di Pitagora.
$$ l^2 = h^2 + \left(\frac{l}{2}\right)^2 $$
$$ l^2 = h^2 + \frac{l^2}{4} $$
Quindi, ricavo l'altezza \( h \):
$$ h^2 = l^2 - \frac{l^2}{4} $$
$$ h^2 = \frac{3l^2}{4} $$
Applico la proprietà invariantiva delle equazioni e calcolo la radice quadrata di entrambi i lati dell'equazione.
$$ \sqrt{ h^2 } = \sqrt{ \frac{3l^2}{4} } $$
$$ h = \sqrt{\frac{3l^2}{2^2}} $$
$$ h = \frac{\sqrt{3}}{2} l $$
Quindi, l'altezza \( h \) di un triangolo equilatero con lato \( l \) è \(\frac{\sqrt{3}}{2} \times l\).
L'ortocentro
L'ortocentro è il punto di incontro delle tre altezze del triangolo
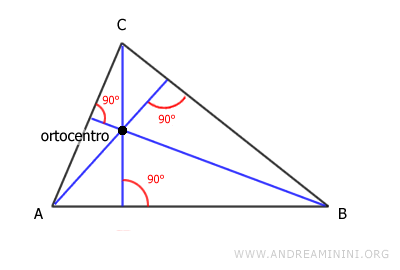
Può trovarsi all'interno o all'esterno del triangolo, oppure su uno dei suoi vertici, a seconda degli angoli:
- All'interno del triangolo
Se il triangolo è acutangolo, ossia se tutti e tre gli angoli del triangolo sono acuti, l'ortocentro si trova all'interno del triangolo.
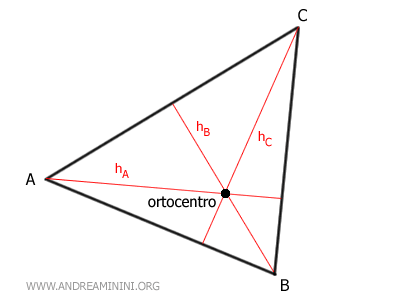
- All'esterno del triangolo
Se il triangolo è ottusangolo, ossia see uno solo degli angoli del triangolo è ottuso, l'ortocentro si trova al di fuori del triangolo.
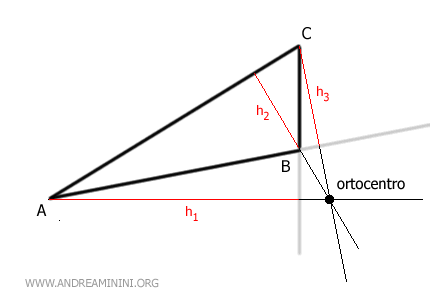
- Su uno dei vertici del triangolo
Se il triangolo è rettangolo, ossia se uno degli angoli misura 90°, l'ortocentro si trova sul vertice corrispondente all'angolo retto.
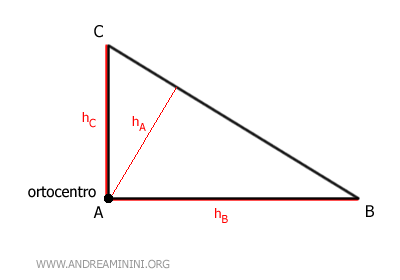
E così via.
