Ortocentro
In un triangolo l'ortocentro è il punto di incontro delle sue tre altezze.
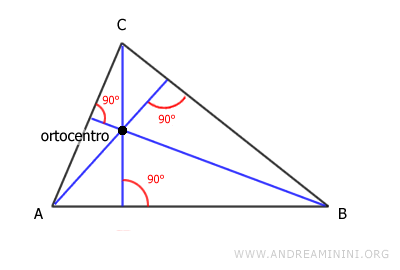
L'altezza è una retta perpendicolare a un lato del triangolo, o alla sua estensione, e che interseca il vertice opposto.
Ogni triangolo ha tre altezze, perché ha tre vertici e tre lati.
Il punto di intersezione di queste tre linee è l'ortocentro.
La posizione dell'ortocentro
La posizione dell'ortocentro dipende dall'ampiezza degli angoli del triangolo.
L'ortocentro di un triangolo può trovarsi:
- All'interno del triangolo se è acutangolo. Se tutti e tre gli angoli del triangolo sono acuti (<90°), l'ortocentro si trova all'interno del triangolo.
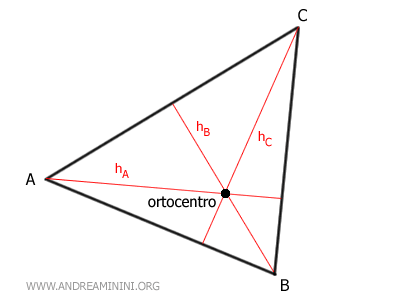
- All'esterno del triangolo se è ottusangolo. Se uno solo degli angoli del triangolo è ottuso (>90°), l'ortocentro si trova all'esterno del triangolo.
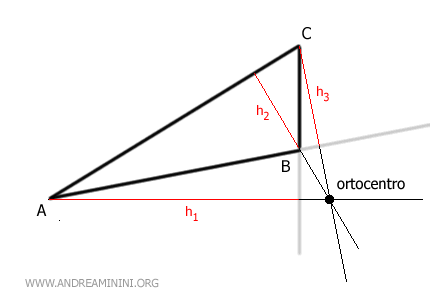
- Su uno dei vertici del triangolo se il triangolo è rettangolo. Nel caso del triangolo rettangolo l'ortocentro si trova su uno dei vertici del triangolo, quello corrispondente all'angolo retto (90°).
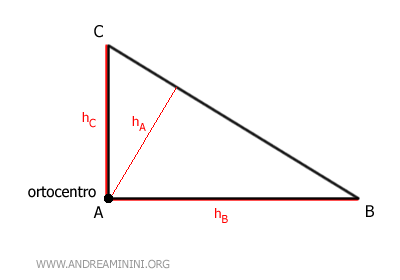
La dimostrazione
Per dimostrare che le altezze si intersecano in un punto comune, considero un triangolo ABC.
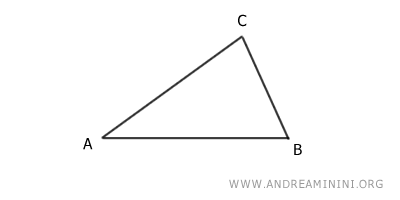
Traccio le rette parallele ai lati del triangolo che passano per il vertice opposto.BC
Le rette parallele a rette incidenti, sono a loro volta rette incidenti che si intersecano nei punti D, E, F.
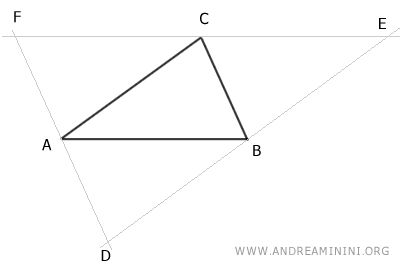
Per costruzione osservo che:
- I segmenti AD||BC e AC||DB sono paralleli e formano un parallelogramma ADBC.
- I segmenti AF||BC e AB||CF sono paralleli e formano un parallelogramma ABCF
Essendo parallelogrammi hanno i lati opposti congruenti AD≅BC, AB≅DB, AF≅BC, AB≅CF
Per la proprietà transitiva sapendo che AD≅BC e AF≅BC deduco che AD≅AF
$$ \overline{AD} \cong \overline{AF} $$
Pertanto, il punto A è il punto medio del lato DF.
Ora traccio l'altezza AG del triangolo ABC perpendicolare al lato BC che passa per il vertice opposto A.
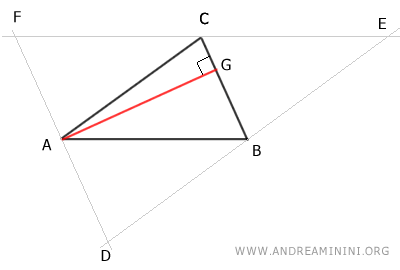
La retta che contiene il segmento AG è perpendicolare anche al lato DF perché DF è un segmento parallelo per costruzione al lato BC.
Quindi, la retta che contiene il segmento AG (altezza del triangolo ABC) è l'asse del triangolo DEF in quanto è perpendicolare al lato DF e passa per il suo punto medio A.
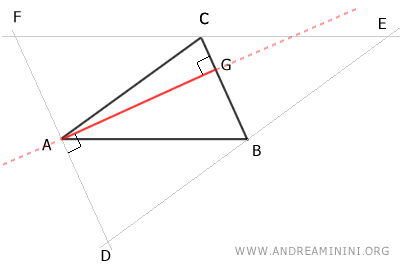
Allo stesso modo posso dimostrare che il punto B è il punto medio del segmento DE.
Per costruzione ci sono due parallelogrammi ADBC e ABEC con i lati opposti congruenti.
Per la proprietà transitiva se DB≅AC e BE≅AC deduco che DB≅BE sono congruenti.
$$ \overline{DB} \cong \overline{BE} $$
Pertanto il punto B è il punto medio del segmento DE.
Ora traccio l'altezza BH del triangolo ABC che è perpendicolare al lato AC e ha per estremo il vertice B.
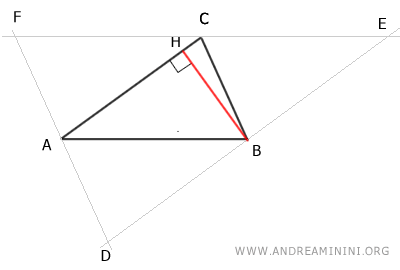
Sapendo che AC||DE sono parallele per costruzione, la retta che comprende il segmento BH è perpendicolare anche al lato DE.
Quindi, l'altezza BH del triangolo ABC coincide con l'asse del lato DE del triangolo DEF.
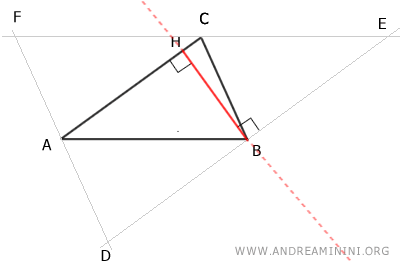
Infine, seguendo la stessa procedura, dimostro che il punto C è il punto medio del segmento EF.
Per costruzione ci sono due parallelogrammi ABCF e ABEC con i lati opposti congruenti.
Per la proprietà transitiva se AB≅CF e AB≅CE deduco che CF≅CE sono segmenti congruenti.
$$ \overline{CF} \cong \overline{CE} $$
Pertanto, se CF≅CE allora il punto C è il punto medio del segmento EF.
A questo punto traccio l'altezza IC del triangolo ABC che è perpendicolare al lato AB e ha per estremo il vertice C.
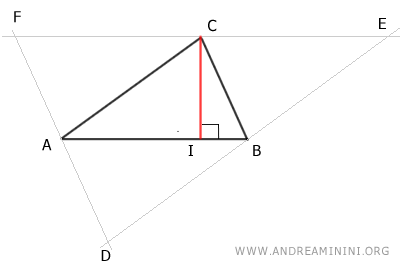
Sapendo che AB||EF sono segmenti paralleli per costruzione, deduco che la retta che comprende il segmento IC è perpendicolare anche al lato EF.
Quindi, l'altezza IC del triangolo ABC coincide con l'asse del lato EF del triangolo DEF.
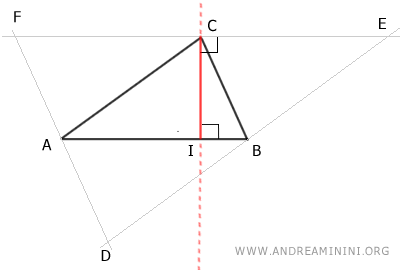
Fin qui ho dimostrato che le altezze del triangolo ABC sono segmenti compresi negli assi del triangolo DEF.
In conclusione, sapendo che gli assi di un triangolo si intersecano sempre in punto comune (vedi dimostrazione del circocentro), deduco che anche le rette che comprendono le altezze di un triangolo si incontrano in punto comune.
In altre parole, le rette che includono le altezze di un triangolo sono parallele agli assi dello stesso triangolo, perché sono perpendicolari allo stesso lato.
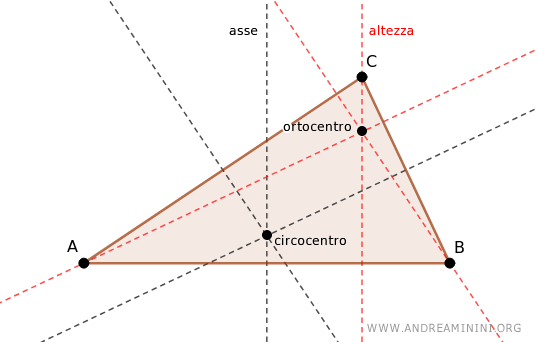
Le rette parallele a rette incidenti sono a loro volta delle rette incidenti.
Quindi, una volta dimostrato che gli assi del triangolo si incontrano sempre in un punto comune (circocentro), posso dedurre che anche le rette che comprendono le altezze del triangolo si intersecano in punto comune (ortocentro).
E così via.
