Il secondo criterio di similitudine dei triangoli
Due triangoli sono simili se hanno due lati corrispondenti in proporzione e l'angolo tra questi congruente.
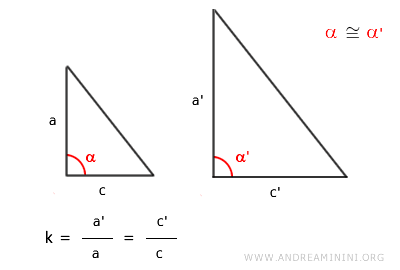
Se due triangoli hanno due lati proporzionali nello stesso ordine e l'angolo adiacente ai lati è congruente, allora i due triangoli sono figure simili.
Questo criterio di similitudine dei triangoli è anche conosciuto come LAL (Lato Angolo Lato).
Un esempio pratico
Prendo come esempio due triangoli ABC e A'B'C'
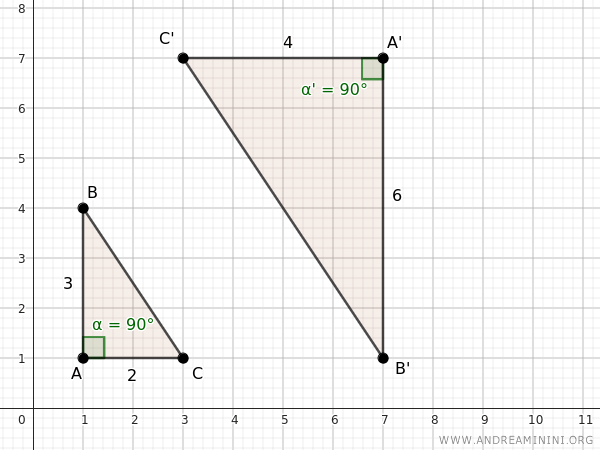
I due triangoli hanno i lati AB e A'B' e i lati AC e A'C' proporzionali
$$ \overline{AB} : \overline{A'B'} = \overline{AC}:\overline{A'C'} $$
che sotto forma di frazione diventa
$$ \frac{ \overline{AB} }{ \overline{A'B'}} = \frac{ \overline{AC} }{ \overline{A'C'}} $$
Sapendo che AB=3, AC=2. A'B'=6, A'C'=5
$$ \frac{ 3 }{ 6} = \frac{ 2 }{ 4} $$
$$ \frac{ 1 }{ 2} = \frac{ 1 }{ 2} $$
Inoltre, hanno l'angolo tra di essi congruente α≅α' in quanto è un angolo retto in entrambi i casi.
$$ \alpha \cong \alpha' $$
In base al secondo criterio di similitudine, i triangoli ABC e A'B'C' sono triangoli simili.
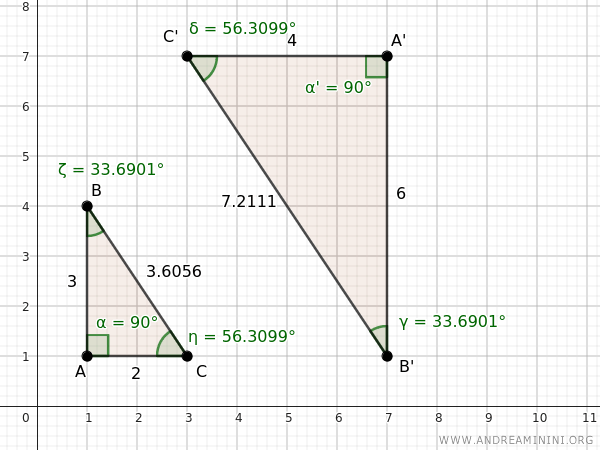
In effetti sono simili perché hanno tutti gli angoli ordinatamente congruenti e tutti i lati corrispondenti proporzionali.
La dimostrazione
Considero due triangoli ABC e A'B'C'
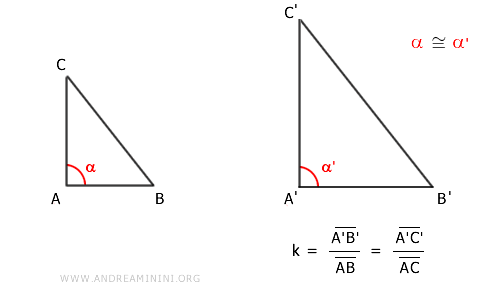
Per ipotesi iniziale, i lati AB e AC del primo triangolo ABC sono proporzionali con i lati A'B' e A'C' del secondo triangolo A'B'C'.
$$ \overline{A'B'} : \overline{AB} = \overline{A'C'} : \overline{AC} $$
ovvero
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{A'C'}}{\overline{AC}} = k $$
Inoltre, per ipotesi iniziale, l'angolo α tra i lati AB e AC è congruente con l'angolo α' tra i lati A'B' e A'C'
$$ \alpha \cong \alpha' $$
Devo dimostrare che i due triangoli sono simili
$$ ABC \approx A'B'C' $$
Per farlo considero due ipotesi che i lati AB e A'B' siano congruenti o non congruenti.
1) I lati AB e A'B' sono congruenti
Se i lati AB≅A'B' sono congruenti, allora per l'ipotesi iniziale anche i lati AC=A'C' sono congruenti
$$ \overline{AB} : \overline{A'B'} = \overline{AC} : \overline{A'C'} $$
Nota. La congruenza AB≅A'B' implica che il rapporto AB/A'B' sia pari a uno. $$ 1 = \overline{AC} : \overline{A'C'} $$ Pertanto, moltiplicando entrambi i membri dell'equazione per A'C' ottengo $$ \overline{A'C'} = \overline{AC} $$ Pertanto, i lati AC e A'C' hanno la stessa lunghezza, ovvero sono congruenti AC≅A'C'
Una volta stabilito che i lati AB≅A'B' e AC≅A'C' sono congruenti, per il primo criterio di congruenza dei triangoli deduco che anche i triangoli ABC e A'B'C' sono congruenti.
$$ ABC \cong A'B'C' $$
Due figure congruenti sono anche figure simili con un rapporto di similitudine pari a 1.
Quindi, i due triangoli sono simili.
$$ ABC \approx A'B'C' $$
2) I lati AB e A'B' non sono congruenti
Se i lati AB e A'B' non sono congruenti, calcolo il rapporto tra i lati
$$ k = \frac{\overline{A'B'}}{AB} $$
Poi costruisco una omotetia con centro A e un rapporto k e ottengo un nuovo triangolo AB"C".
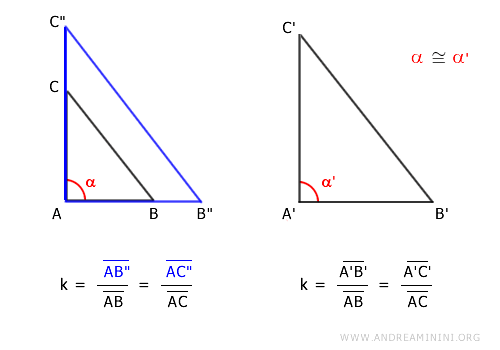
Nota. Ho scelto appositamente il punto A come centro dell'omotetia per semplificare la dimostrazione. In questo modo l'angolo α è una proprietà invariante della trasformazione geometrica. Mi farà comodo nel resto della dimostrazione. Avrei potuto scegliere qualsiasi altro punto, il risultato finale sarebbe stato lo stesso ma la dimostrazione un po' più lunga.
Nel nuovo triangolo il punto A è un punto fisso della trasformazione geometrica perché non cambia.
Per costruzione dell'omotetia i lati AB e AB" e i lati AC e AC" sono proporzionali con un rapporto k
$$ \frac{\overline{AB"}}{\overline{AB}} = \frac{\overline{AC"}}{\overline{AC}} = k $$
Sapendo per ipotesi iniziale che vale questa proporzione
$$ \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{A'C'}}{\overline{AC}} = k $$
Deduco che A'B'≅AB" e A'C'=AC" sono segmenti congruenti.
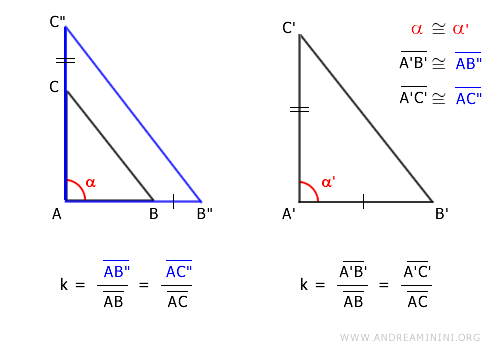
Per l'ipotesi iniziale anche l'angolo α≅α' è congruente.
Quindi, i due triangoli A'B'C'≅AB"C" sono congruenti per il primo criterio di congruenza dei triangoli, in quanto hanno due lati congruenti A'B'≅AB" e A'C'=AC" e l'angolo α≅α' tra questi congruente.
$$ A'B'C' \cong AB"C" $$
Sapendo che il triangolo AB"C" è simile al triangolo ABC perché ogni trasformazione omotetica è anche una similitudine.
$$ AB"C" \approx ABC $$
Spiegazione. Una similitudine è una composizione tra una omotetia e una isometria o viceversa. Quindi, posso vedere la similitudine come la composizione di un'omotetia e di una identità (isometria). Ne consegue che la trasformata omotetica di una figura è simile alla figura iniziale ovvero il triangolo AB"C" è simile al triangolo ABC. $$ AB"C" \approx ABC $$
Poiché A'B'C'≅AB"C" deduco che il triangolo A'B'C' è simile al triangolo ABC.
$$ A'B'C' \approx ABC $$
3) Conclusione
In entrambe le ipotesi, i lati AB e A'B' congruenti e non congruenti, i triangoli ABC e A'B'C' sono figure simili.
Questo dimostra il secondo criterio di similitudine dei triangoli.
E così via.
