Criteri di similitudine dei triangoli
I criteri di similitudine del triangolo forniscono le condizioni sufficienti affinché due triangoli siano simili.
Sono molto utili perché mi permettono di verificare la similitudine tra due triangoli senza dover analizzare tutte le loro caratteristiche.
Esistono tre diversi criteri di similitudine.
Il primo criterio di similitudine
Due triangoli sono simili se due angoli corrispondenti sono congruenti.
Se i triangoli hanno due angoli interni congruenti nello stesso ordine, allora anche il terzo angolo interno è congruente.
Pertanto, i due triangoli hanno la stessa forma nel piano ma possono differire per dimensione.
E' anche detto criterio di similitudine AAA dei triangoli ovvero Angolo-Angolo-Angolo
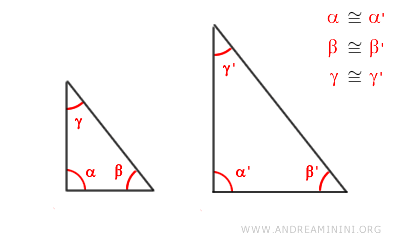
Ad esempio, se i due triangoli hanno due angoli corrispondenti α≅α' e β≅β' congruenti
$$ \alpha \cong \alpha ' $$
$$ \beta \cong \beta ' $$
Allora i due triangoli soddisfano il criterio di similitudine e sono triangoli simili.
Nota. In un triangolo è sufficiente verificare che qualsiasi coppia di angoli corrispondenti siano congruenti, perché la somma degli angoli interni di un triangolo è sempre uguale a 180°. Quindi, se due triangoli hanno due angoli congruenti α≅β, anche il terzo angolo sarà congruente per differenza da 180° ossia γ≅180°-α-β. Lo stesso vale per qualsiasi coppia di angoli interni corrispondenti.
Il secondo criterio di similitudine
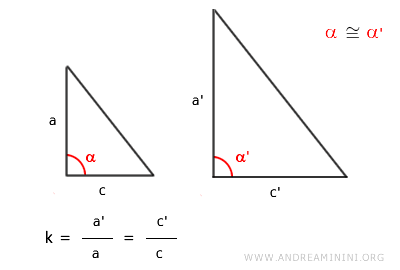
Due triangoli sono simili se hanno due lati corrispondenti in proporzione e l'angolo tra di essi congruente.
Se due triangoli hanno due lati ordinatamente proporzionali, nella stessa proporzione k, e l'angolo tra i due lati è congruente, allora sono due triangoli simili.
E' anche indicato come criterio di similitudine LAL (Lato-Angolo-Lato) dei triangoli.
Il terzo criterio di similitudine
Due triangoli sono simili se hanno tutti i lati corrispondenti nella stessa proporzione.
Se due triangoli hanno tutti i lati ordinatamente proporzionali, nella stessa proporzione k, allora sono due triangoli simili.
E' anche conosciuto come il criterio di similitudine LLL (Lato-Lato-Lato) dei triangoli.
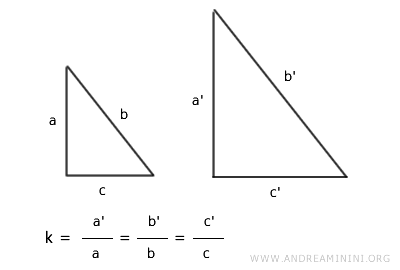
E così via.
