La distanza di un punto da una retta

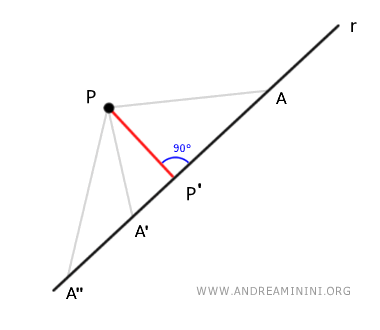
La distanza di un punto P da una retta è la lunghezza del segmento che ha per estremi il punto P e il piede della perpendicolare (P').

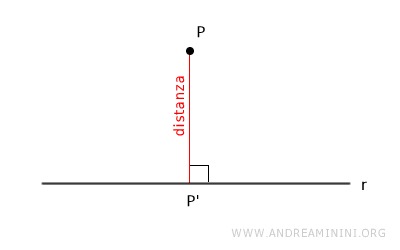
In altre parole, la distanza è uguale alla lunghezza della proiezione ortogonale del punto sulla retta.

Qualsiasi altro segmento obliquo tra il punto P e un punto della retta ha una lunghezza maggiore rispetto alla distanza.

La dimostrazione

Per dimostrarlo basta prendere un qualsiasi altro punto della retta diverso da P'. Ad esempio, il punto A.

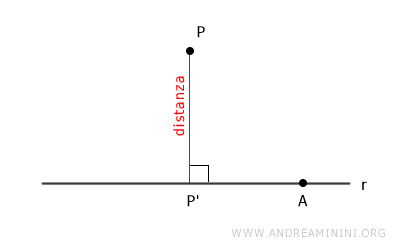
Il segmento AP che congiunge i punti P e A è obliquo rispetto alla perpendicolare.

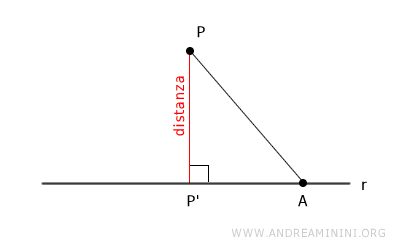
La lunghezza del segmento AP è sicuramente inferiore rispetto al segmento PP' (distanza) perché i punti PP'A formano un triangolo rettangolo.

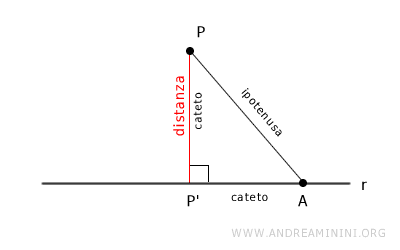
Secondo il teorema di Pitagora, in un triangolo rettangolo ogni singolo cateto ha una lunghezza inferiore rispetto all'ipotenusa.

Pertanto, il segmento AP non può essere la distanza del punto P e la retta r, perché la lunghezza del segmento PP' è sempre minore.

In generale, lo stesso discorso vale per qualsiasi segmento AP, ovvero per qualunque punto A sulla retta r diverso da P'.

Per un approfondimento della distanza tra un punto e la retta usando le equazioni vettoriali, rimando alla lettura di un altro mio appunto universitario: come calcolare la distanza tra un punto e una retta con i vettori. Il resto di questo appunto è limitato al piano e alle conoscenze della geometria analitica liceale.

Il calcolo della distanza tra un punto e una retta sul piano

In geometria analitica la distanza tra un punto P(x₀;y₀) e una retta r sul piano si ottiene usando questa formula: $$ d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

Dove $ ax+by+c=0 $ è l'equazione generale della retta r mentre (x₀;y₀) sono le coordinate del punto P.

Un esempio pratico

Considero questa retta sul piano cartesiano:

$$ 2x + 4y -6 = 0 $$

e un punto A che si trova alle seguenti coordinate:

$$ A \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

Per semplicità rappresento sia il punto A che la retta sul piano cartesiano.

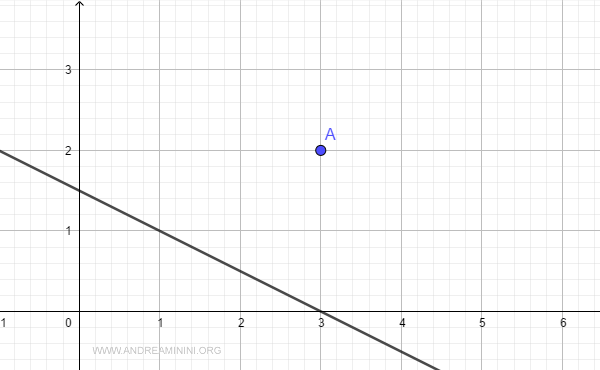
Qual è la distanza tra il punto e la retta?

Per trovare la distanza tra il punto A e la retta r applico la formula iniziale

$$ d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$

Nella formula sostituisco le coordinate del punto A(x₀;y₀)=(3;2) ovvero x₀=3 e y₀=2.

$$ d = \frac{|a(3)+b(2)+c|}{\sqrt{a^2+b^2}} $$

Sostituisco nella formula anche i coefficienti dell'equazione generale della retta $ 2x + 4y -6 = 0 $ che in questo caso sono a=2, b=4 e il termine noto c=-6.

$$ d = \frac{|2 \cdot (3)+4 \cdot (2)-6|}{\sqrt{2^2+4^2}} $$

Infine, svolgo i calcoli algebrici

$$ d = \frac{|6+8-6|}{\sqrt{4+16}} $$

$$ d = \frac{8}{\sqrt{20}} $$

$$ d = 1.78 $$

Quindi la distanza minima tra il punto A e la retta è 1,78.

Faccio una rapida verifica su Geogebra e il risultato è corretto. La distanza d è il segmento AH perpendicolare (90°) alla retta che ha come estremo il punto A(3;2) ed è lungo circa 1.78.

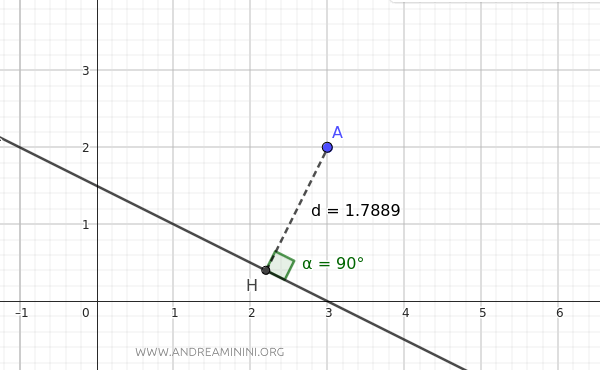
Dimostrazione

Per dimostrare la formula della distanza considero una retta $ ax+by+c=0 $ e un punto qualsiasi del piano $ P(x_0;y_0) $

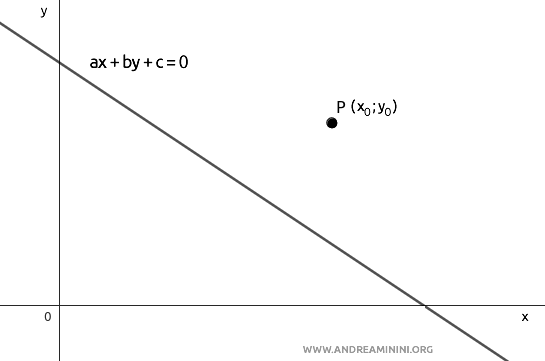
So già che geometricamente la distanza è il segmento $ \overline{PH} $ perpendicolare alla retta che ha per estremi il punto P e un punto $ H $ della retta.

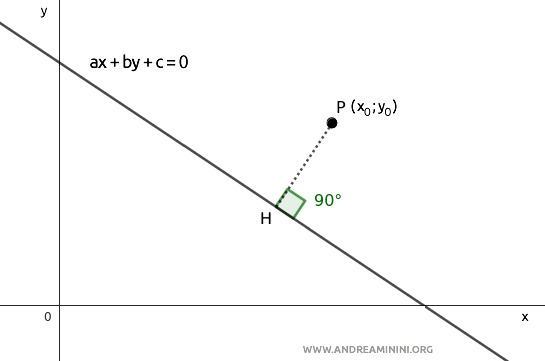
Traccio due rette parallele agli assi cartesiani che passano per il punto P.

In questo modo individuo due punti di intersezione A e B con la retta.

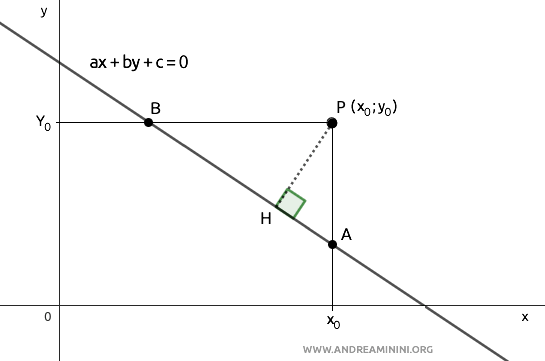
Il punto A appartiene alla retta $ ax+by+c=0 $ e ha la stessa componente x₀ del punto P.

Quindi, posso sostituire x con x₀ nell'equazione generale della retta.

$ ax_0+by+c=0 $

Questo mi permette di ricavare il valore della y.

$$ y =  \frac{-ax_0-c}{b} = - \frac{ax_0+c}{b} $$

In questo modo ottengo le coordinate del punto A.

$$ A = ( x_0 ; - \frac{ax_0+c}{b} ) $$

Faccio un ragionamento analogo per il punto B.

Anche il punto B appartiene alla retta $ ax+by+c=0 $ e ha la stessa componente y₀ del punto P.

Quindi, sostituisco y con y₀ nell'equazione generale della retta.

$ ax+by_0+c=0 $

E ricavo il valore della x.

$$ x =  \frac{-by_0-c}{a} = - \frac{by_0+c}{a} $$

In questo modo ottengo anche le coordinate del punto B.

$$ B = (  - \frac{by_0+c}{a} ; y_0 ) $$

Nel piano i punti A, B e P formano un triangolo ABP

Il triangolo ABP è un triangolo rettangolo perché i suoi cateti sono coincidenti con le rette parallele agli assi cartesiani che formano un angolo di 90°.

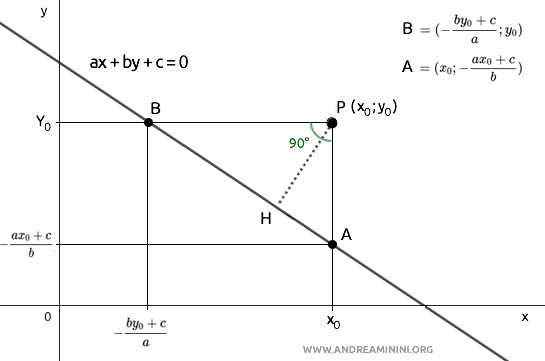
In un triangolo rettangolo l'altezza $ \overline{PH} $ rispetto all'ipotenusa è uguale al rapporto tra il prodotto dei cateti $ \overline{AP} \cdot \overline{BP}  $ e l'ipotenusa $ \overline{AB}  $.

$$ \overline{PH} = \frac{\overline{AP} \cdot \overline{BP} }{ \overline{AB} } $$

Spiegazione. Questa formula deriva dal fatto in un triangolo qualsiasi l'altezza è uguale al rapporto tra il doppio dell'area e la lunghezza della base. $$ h = \frac{2 \times \text{area}}{ \text{base} } $$ Nel caso del triangolo rettangolo l'area posso calcolarla tramite il semiprodotto dei cateti e indicando come base l'ipotenusa $$ h = \frac{2 \times ( \frac{ \overline{AP} \cdot \overline{BP} }{2} ) }{  \overline{AB} } $$ $$ h = \frac{ \overline{AP} \cdot \overline{BP} }{  \overline{AB} } $$

A questo punto, per conoscere la distanza PH devo prima calcolare le lunghezze dei segmenti AP, BP, AB.

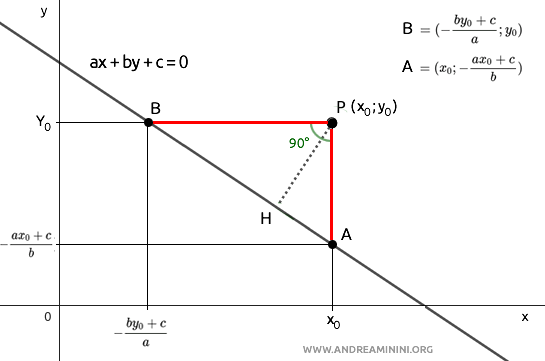
E' abbastanza semplice per i cateti AP e BP poiché conosco le coordinate dei punti A e B.

$$ \overline{AP} = | y_0 - (  - \frac{ax_0+c}{b} ) | = | \frac{ax_0+by_0+c}{b} |  $$

$$ \overline{BP} =|  x_0 - ( - \frac{by_0+c}{a} ) | = | \frac{ax_0+by_0+c}{a}  | $$

Per calcolare l'potenusa AB utilizzo, invece, il teorema di Pitagora e svolgo qualche passaggio algebrico.

$$ \overline{AB} = \sqrt{ \overline{AP}^2 + \overline{BP}^2} $$

$$ \overline{AB} = \sqrt{ (  | \frac{ax_0+by_0+c}{b} |  )^2 + ( | \frac{ax_0+by_0+c}{a}  | ) ^2} $$

$$ \overline{AB} = \sqrt{  \frac{(ax_0+by_0+c)^2}{b^2}  +  \frac{(ax_0+by_0+c)^2}{a^2} }  $$

$$ \overline{AB} = \sqrt{  (ax_0+by_0+c)^2  \cdot ( \frac{1}{b^2}  +  \frac{1}{a^2} ) }  $$

$$ \overline{AB} = |ax_0+by_0+c|  \cdot \sqrt{  \frac{a^2+b^2}{a^2b^2}  }  $$

$$ \overline{AB} = \frac{ |ax_0+by_0+c| }{ |ab| }  \cdot \sqrt{  a^2+b^2  }  $$

Una volta trovate le lunghezze dei segmenti AP, BP e AB li sostituisco nell'equazione per calcolare la distanza PH

$$ \overline{PH} = \frac{\overline{AP} \cdot \overline{BP} }{ \overline{AB} } $$

$$ \overline{PH} = \frac{ | \frac{ax_0+by_0+c}{b} |  \cdot | \frac{ax_0+by_0+c}{a}  | }{  \frac{ |ax_0+by_0+c| }{ |ab| }  \cdot \sqrt{  a^2+b^2  } } $$

$$ \overline{PH} = \frac{ | \frac{ax_0+by_0+c}{b} |  \cdot | \frac{ax_0+by_0+c}{a}  | }{  \frac{ |ax_0+by_0+c| }{ |ab| }  \cdot \sqrt{  a^2+b^2  } } \cdot \frac{ |ab|  }{ } $$

$$ \overline{PH} =  | \frac{ax_0+by_0+c}{b} |  \cdot | \frac{ax_0+by_0+c}{a}  |  \cdot \frac{ |ab|  }{  |ax_0+by_0+c| \cdot \sqrt{  a^2+b^2  } } $$ 

Sapendo che il modulo di un prodotto |ab| è uguale al prodotto dei moduli |a|·|b|

$$ \overline{PH} =  | \frac{ax_0+by_0+c}{b} |  \cdot | \frac{ax_0+by_0+c}{a}  |  \cdot \frac{ |a| \cdot |b|  }{  |ax_0+by_0+c| \cdot \sqrt{  a^2+b^2  } } $$

Inoltre, il modulo di un rapporto è uguale al rapporto dei moduli.

$$ \overline{PH} =   \frac{|ax_0+by_0+c|}{|b|}  \cdot  \frac{|ax_0+by_0+c|}{|a|}   \cdot \frac{ |a| \cdot |b|  }{  |ax_0+by_0+c| \cdot \sqrt{  a^2+b^2  } } $$

A questo punto semplifico

$$ \require{cancel} \overline{PH} =   \frac{|ax_0+by_0+c|}{\cancel{ |b| }}  \cdot  \frac{ \cancel{ |ax_0+by_0+c| } }{ \cancel{ |a| }}   \cdot \frac{ \cancel{|a|} \cdot \cancel{|b|}  }{  \cancel{|ax_0+by_0+c|} \cdot \sqrt{  a^2+b^2  } } $$

E ottengo la formula della distanza tra il punto e la retta che volevo dimostrare

$$ \require{cancel} \overline{PH} =    \frac{|ax_0+by_0+c|  }{      \sqrt{  a^2+b^2  } } $$

E così via.