Relazione tra lati e angoli opposti di un triangolo
In un triangolo c'è una stretta relazione tra i lati e gli angoli opposti.
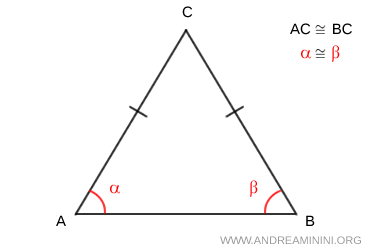
- Se in un triangolo due lati sono congruenti anche gli angoli opposti sono congruenti. Ad esempio, un triangolo isoscele ha due lati congruenti e gli angoli opposti agli stessi lati congruenti tra loro.
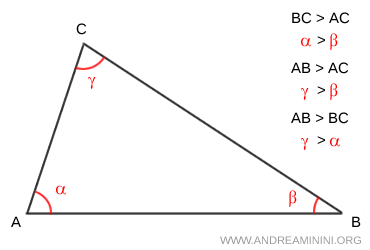
- Se in un triangolo due lati non sono congruenti, allora anche gli angoli opposti non sono congruenti e al lato maggiore sta opposto l'angolo maggiore.
La dimostrazione
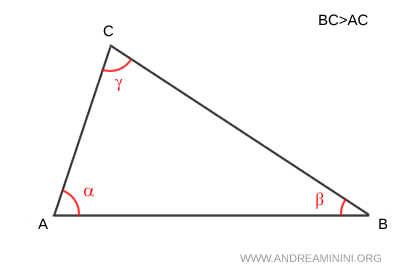
Considero per ipotesi che il triangolo abbia un lato maggiore di un altro.
$$ BC>AC $$
Devo dimostrare che l'angolo $ \alpha $ opposto a $ BC $ ha un'ampiezza maggiore dell'angolo $ \beta $ opposto ad $ AC $.
Poiché $ BC>AC $, deve esistere sul lato BC un punto P tale che $ AB \cong CP $.
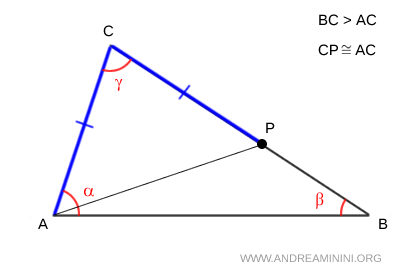
Ora per costruzione il triangolo ACP è un triangolo isoscele perché ha due lati congruenti $ AB \cong CP $, quindi ha gli angoli $ \theta $ alla base congruenti.
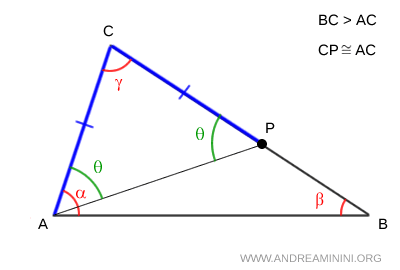
Poiché il segmento $ AP $ taglia l'angolo $ \alpha $, posso dedurre che ha un'ampiezza maggiore dell'angolo $ \theta $.
$$ \alpha > \theta $$
Guardando il triangolo $ APC $ noto che l'angolo $ \theta $ è anche un angolo esterno.
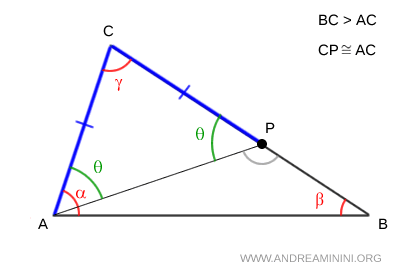
Per il teorema degli angoli esterni, in un triangolo un angolo esterno è sempre maggiore degli agli altri due angoli interni non adiacenti.
Quindi, l'angolo $ \theta $ ha un'ampiezza maggiore di $ \beta $.
$$ \theta > \beta $$
Ricapitolando, ho dimostrato che sussiste questa relazione tra gli angoli
$$ \alpha > \theta > \beta $$
Dove $ \alpha $ è l'angolo opposto al lato $ BC $ che per ipotesi è maggiore di $ AC $, mentre $ \beta $ è l'angolo opposto di $ AC $.
Ho dimostrato che l'angolo opposto al lato maggiore ( $ BC>AC $ ) ha un'ampiezza maggiore ( $ \alpha > \beta $ ).
Il teorema inverso
In un triangolo, se due angoli non sono congruenti, allora il lato opposto all'angolo maggiore è più lungo del lato opposto all'angolo minore.
Come conseguenza di questo principio:
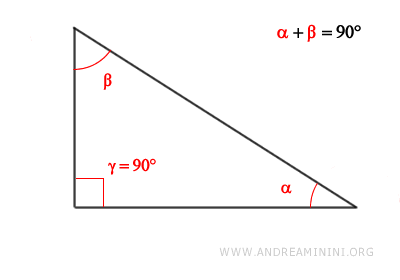
- In un triangolo rettangolo, l'ipotenusa è sempre il lato più lungo, poiché è opposta all'angolo retto (90°), che è il più grande del triangolo.
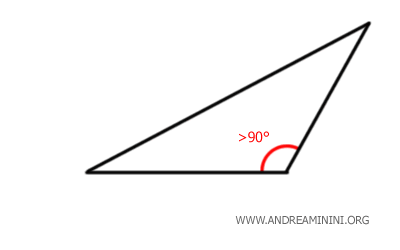
- In un triangolo ottusangolo, il lato opposto all'angolo ottuso (maggiore di 90°) è sempre più lungo di ciascuno degli altri due lati.
E così via.
