Il teorema dell'angolo esterno di un triangolo
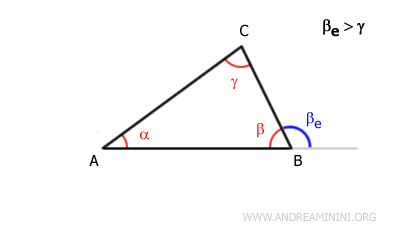
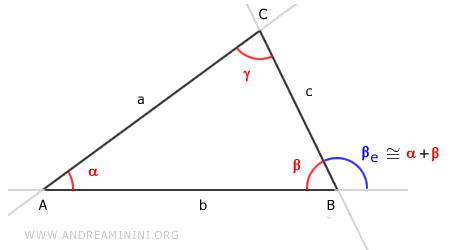
In un triangolo ogni angolo esterno (βe) ha un'ampiezza maggiore rispetto agli angoli interni non adiacenti (α e γ)
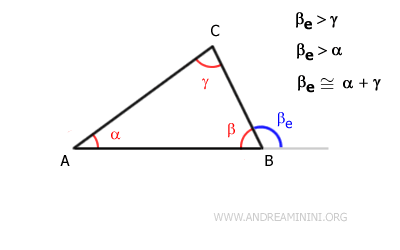
perché ogni angolo esterno di un triangolo è congruente alla somma degli angoli interni non adiacenti $$ \beta_e \cong \alpha + \gamma $$
E' un teorema generale che vale per qualsiasi triangolo.
Ad esempio, nel triangolo ABC l'angolo esterno del vertice B, ossia βe, è maggiore sia dell'angolo interno α che dell'angolo interno γ.

Quindi, nel triangolo ABC l'angolo esterno βe ha un'ampiezza maggiore rispetto a ogni altro angolo interno diverso dall'angolo β.
Dimostrazione
Considero un triangolo ABC.
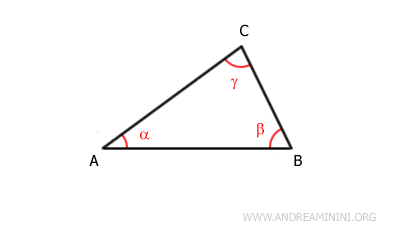
Prolungo il segmento AB e individuo l'angolo esterno $ \beta_e $ rispetto all'angolo interno $ \beta $.
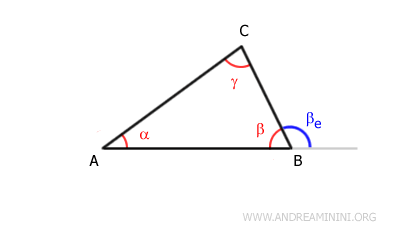
Traccio un segmento $ BE $ parallelo al segmento $ AC $ passante per il vertice $ B $.
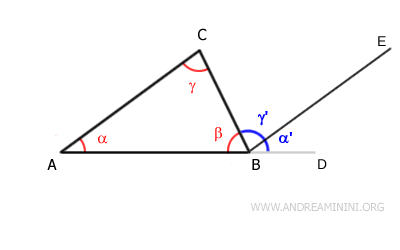
Per costruzione, l'angolo esterno $ \beta_e $ è la somma degli angoli $ \alpha'$ e $ \gamma' $.
$$ \beta_e = \alpha' + \gamma' $$
In base al teorema delle rette parallele, poiché le rette passanti per $ BE $ e per $ AC $ sono parallele con una trasversale $ CB $, gli angoli alterni interni sono congruenti
$$ \gamma = \gamma' $$
Le rette parallele passanti per $ BE $ e per $ AC $ sono intersecate anche dalla trasversale $ AB $ e sempre in base al teorema delle rette parallele gli angoli corrispondenti sono congruenti
$$ \alpha = \alpha' $$
Nota. Ho applicato lo stesso teorema sulle rette parallele passanti per $ BE $ e $ AC $ ma utilizzando una diversa trasversale. Nel primo caso la trasversale passa per il segmento $ CB $ mentre nel secondo caso la trasversale passa per $ AB $.
Questo vuol dire che l'angolo esterno $ \beta_e $ è pari alla somma degli angoli interni del triangolo non adiacenti con $ \beta $.
$$ \beta_e = \alpha' + \gamma' = \alpha + \gamma $$
Poiché $\beta_e = \alpha + \gamma$, allora l'angolo esterno $ \beta_e $ è necessariamente maggiore sia di $\alpha$ che di $\gamma$ presi singolarmente."
$$ \beta_e > \alpha $$
$$ \beta_e > \gamma $$
Questo dimostra che l'angolo esterno è maggiore degli angoli interni non adiacenti ed è congruente alla loro somma.
Dimostrazione alternativa
A] L'angolo esterno è maggiore degli angoli interni non adiacenti
Considero un generico triangolo ABC

Prendo in considerazione l'angolo esterno del vertice B che da adesso in poi chiamo βe

Devo dimostrare che l'angolo esterno βe è maggiore degli angoli interni non adiacenti α e γ.
Prima parte
Individuo il punto medio M nel lato BC adiacente all'angolo β e traccio la mediana AM.
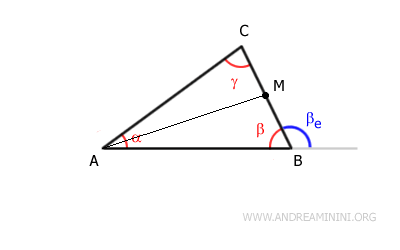
In questo modo ottengo due segmenti congruenti BM e CM
$$ BM \cong CM $$
Prolungo il segmento AM aggiungendo un altro segmento ME congruente, AM=ME. In pratica lo raddoppio
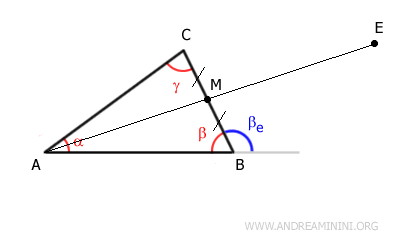
Ricapitolando, i seguenti lati sono congruenti
$$ BM \cong CM $$
$$ AM \cong ME $$
Unisco i punti B ed E aggiungendo il segmento BE alla costruzione.
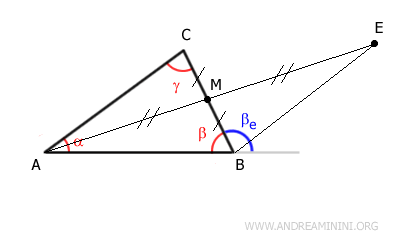
Nel punto M si intersecano due segmenti formando due angoli opposti al vertice congruenti θ1≅θ2
$$ \ θ_1 \cong θ_2 $$
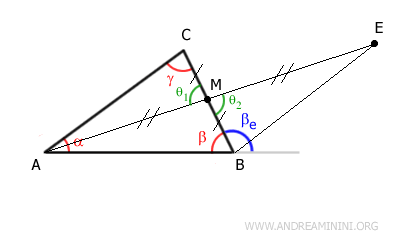
Pertanto, in base al primo teorema della congruenza i due triangoli AMC e BME sono congruenti, perché hanno due lati congruenti BM≅CM e AM≅ME e l'angolo tra di essi congruente θ1≅θ2.
$$ AMC \cong BME $$
Quindi, i due triangoli AMC e BME hanno i lati e gli angoli congruenti nello stesso ordine.
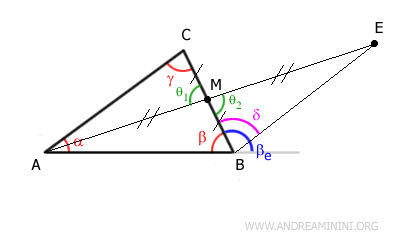
In particolar modo, per concludere la dimostrazione mi interessa sapere che siano congruenti gli angoli γ e δ
$$ \gamma \cong \delta $$
L'angolo δ è minore rispetto all'angolo esterno βe, perché il segmento BE taglia l'angolo βe
$$ \delta < \beta_e $$
Sapendo che gli angoli γ e δ sono congruenti (γ≅δ) , deduco che anche l'angolo γ è minore rispetto all'angolo esterno βe
$$ \gamma < \beta_e $$
Pertanto, l'angolo esterno βe è maggiore rispetto all'angolo interno γ
Seconda parte
A questo punto devo ripetere la stessa operazione per dimostrare che anche l'angolo esterno βe è maggiore anche dell'altro angolo interno non adiacente, ossia dell'angolo α.
Individuo il punto medio M nel segmento AB adiacente all'angolo β e traccio la mediana CM
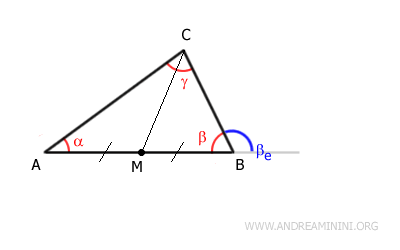
Di conseguenza i due segmenti AM e BM sono congruenti
$$ \overline{AM} \cong \overline{BM} $$
Prolungo il segmento CM aggiungendo un altro segmento MF della stessa lunghezza
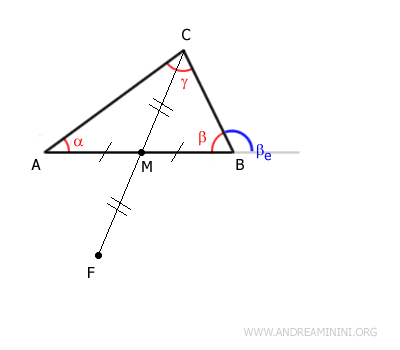
Pertanto, i due segmenti CM e MF sono congruenti
$$ \overline{CM} \cong \overline{MF} $$
Ricapitolando, i seguenti lati sono congruenti
$$ \overline{AM} \cong \overline{BM} $$
$$ \overline{CM} \cong \overline{MF} $$
Unisco i punti B e F aggiungendo il segmento BF alla costruzione.
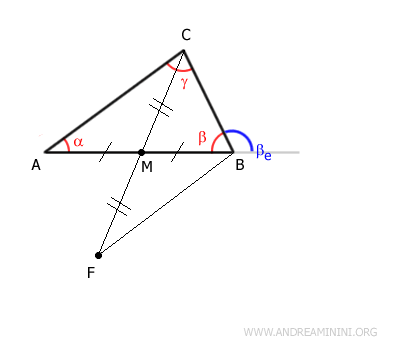
Nel punto M si intersecano due segmenti AB e CF formando due angoli opposti al vertice congruenti θ1≅θ2
$$ θ_1 \cong θ_2 $$
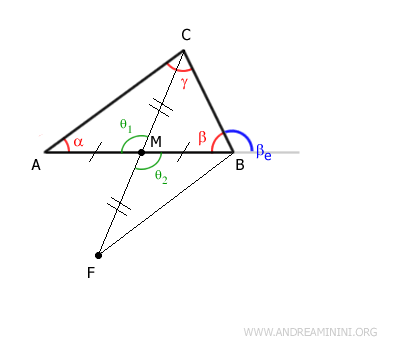
Di conseguenza, in base al primo teorema di congruenza, i triangoli AMC e BMF sono congruenti, perché hanno due lati congruenti CM≅FM e AM≅BM e l'angolo tra di essi congruente θ1≅θ2
$$ AMC \cong BMF $$
Quindi, triangoli AMC e BMF hanno gli stessi angoli e lati congruenti nello stesso ordine.
In particolar modo, mi interessa sapere che l'angolo α è congruente con l'angolo δ (viola)
$$ \alpha \cong \delta $$
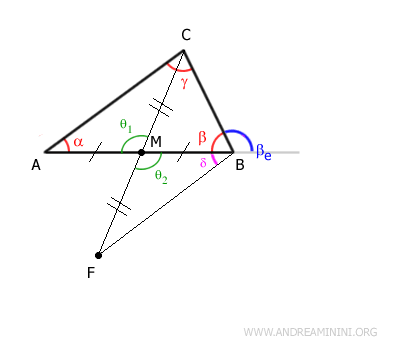
Per confrontare l'angolo βe con l'angolo δ, prolungo il segmento BC
Poi sapendo che gli angoli opposti al vertice sono uguali, proietto un angolo congruente a βe
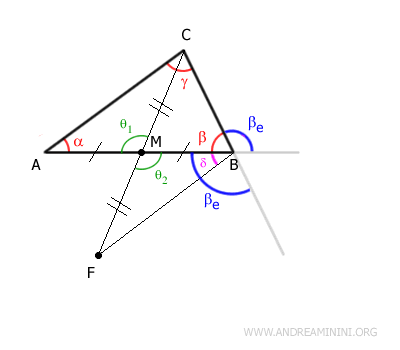
In questo modo è subito evidente che l'angolo esterno βe è maggiore dell'angolo δ, perché il segmento BF taglia l'angolo βe
$$ \delta < \beta_e $$
Sapendo che l'angolo δ è congruente con l'angolo interno α ( δ≅α ), deduco che l'angolo esterno βe è maggiore dell'angolo interno α.

In conclusione
Nel triangolo l'angolo esterno βe ha un'ampiezza maggiore rispetto agli angoli interni non adiacenti α e γ.
Questo dimostra il teorema dell'angolo esterno di un triangolo.
B] L'angolo esterno è congruente alla somma degli angoli interni non adiacenti
A questo punto devo dimostrare che l'angolo esterno è congruente alla somma degli angoli interni non adiacenti.
Considero il triangolo ABC e l'angolo esterno βe
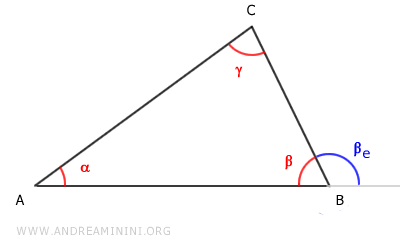
Traccio delle rette passanti per i segmenti del triangolo e le chiamo a, b, c
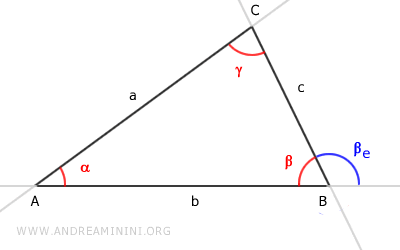
Traccio la retta d parallela al segmento AC che passa per il vertice B del triangolo.
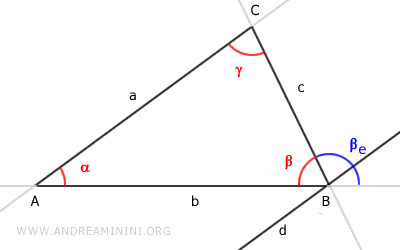
A questo punto posso considerare l'angolo esterno come la somma di due angoli βe=βe'+βe''
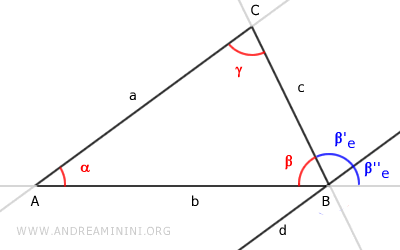
L'angolo β'e è un angolo alterno interno delle rette parallele a||d tagliate dalla retta c.
Per il teorema delle rette parallele gli angoli alterni interni γ e β'e sono congruenti ossia γ≅β'e.

L'angolo β''e è un angolo corrispondente delle rette parallele a||d tagliate dalla retta b.
Per il teorema delle rette parallele gli angoli corrispondenti α e β''e sono congruenti ossia α≅β''e.
Sapendo che l'angolo esterno è la somma βe=βe'+βe'' e gli angoli γ≅β'e e α≅β''e sono congruenti
$$ \begin{cases} \beta_e \cong \beta'_e + \beta''_e \\ \\ \gamma \cong \beta'_e \\ \\ \alpha \cong \beta''_e \end{cases} $$
Deduco che l'angolo esterno βe è congruente alla somma degli angoli interni non adiacenti α+β del triangolo.
$$ \beta_e \cong \beta'_e + \beta''_e $$
$$ \beta_e \cong \beta + \alpha $$
Pertanto, l'angolo esterno βe=α+β ha un'ampiezza pari alla somma degli angoli interni non adiacenti del triangolo.
Note
Alcune note aggiuntive e corollari sull'argomento.
- La somma degli angoli interni di un triangolo è 180°
La somma delle ampiezze degli angoli interni di un triangolo è sempre pari a 180°, cioè a un angolo piatto. In altre parole, è un invariante geometrico, qualcosa che non cambia mai, indipendentemente dal tipo e dalla forma del triangolo.
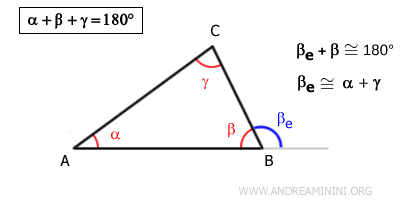
Dimostrazione. Questo risultato si ricava osservando che ciascun angolo interno e il suo angolo esterno corrispondente formano insieme un angolo piatto. Ad esempio $$ \beta + \beta' = 180° $$.Poiché l'angolo esterno è congruente alla somma degli angoli interni non adiacenti, cioè: $ \beta' = \alpha + \gamma $ Deduco che la somma degli angoli interni è sempre congruente a un angolo piatto. $$ \beta + (\alpha + \gamma)= 180° $$ $$ \alpha + \beta + \gamma= 180° $$
- La somma di due angoli interni è sempre minore di un angolo piatto
Questo importante corollario si deduce dal fatto che un angolo esterno del triangolo è maggiore rispetto a ogni angolo interno non adiacente. Ad esempio, $ \alpha + \gamma < 180° $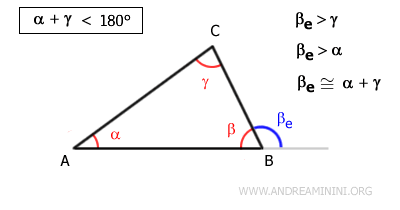
Dimostrazione. Dal teorema dell'angolo esterno so già che l'angolo esterno \( \beta_e \) è maggiore dell'angolo interno non adiacente \( \gamma \) $$ \gamma < \beta_e $$ Aggiungo l'angolo \( \beta \) a ciascun membro della disuguaglianza. $$ \gamma + \beta < \beta_e + \beta $$ Gli angoli \( \beta \) e \( \beta_e \) sono supplementari, quindi la loro somma $ \beta + \beta_e = 180° $ è un angolo piatto $$ \gamma + \beta < 180° $$ Questo dimostra che la somma di due angoli interni qualsiasi di un triangolo è inferiore a un angolo piatto. Con la stessa procedura si dimostra che anche le somme degli altri angoli interni $ \alpha + \gamma $ e $ \alpha + \beta $ sono inferiori a 180°.
- Un triangolo può avere al massimo un angolo retto o un angolo ottuso
Un triangolo può avere al massimo un angolo retto o un angolo ottuso si basa sul fatto che la somma degli angoli interni di un triangolo è sempre 180°.Nota. Se un triangolo avesse due angoli retti (90° + 90° = 180°), non resterebbe spazio per un terzo angolo, il che è impossibile. Se un triangolo avesse due angoli ottusi (cioè ciascuno maggiore di 90°), la loro somma supererebbe i 180°, il che è anch'esso impossibile. Quindi, un triangolo può avere al massimo un solo angolo retto o un solo angolo ottuso. Gli altri due angoli, per completare i 180°, saranno sempre acuti (minori di 90°).
- Altri corollari
Il teorema dell'angolo esterno è alla base di molti utili corollari sui triangoli:- In un triangolo rettangolo gli angoli acuti sono angoli complementari
Sapendo che la somma degli angoli interni è 180°, se un angolo è 90° allora anche la somma degli altri due angoli interni deve essere un angolo retto (90°) - In un triangolo equilatero ogni angolo ha un'ampiezza di 60°
Un triangolo equilatero ha tutti i lati e gli angoli congruenti. Sapendo che la somma degli angoli interni di un triangolo è un angolo piatto (180°), dividendo 180° tra i tre angoli si ottiene che ogni angolo interno deve avere un'ampiezza di 60°. - Se due triangoli hanno due angoli interni congruenti, allora anche l'angolo interno rimanente è congruente. Poiché la somma degli angoli interni di un triangolo è sempre 180°. Quindi, se due triangoli hanno due angoli congruenti, anche il terzo angolo deve esserlo.
Nota. Questo corollario è alla base del secondo criterio generalizzato di congruenza dei triangoli. Se due triangoli hanno due angoli congruenti $ \alpha \cong \alpha' $ e $ \beta \cong \beta' $ e un lato congruente $ BC \cong B'C' $ nello stesso ordine, allora sono triangoli congruenti $ ABC \cong A'B'C' $ anche se gli angoli non sono adiacenti al lato in questione. Questo accade perché anche il terzo angolo $ \gamma \cong \gamma ' $ è congruente, essendo la somma degli angoli interni sempre pari a 180°. Quindi, esistono due angoli congruenti ( $ \beta \cong \beta' $ e $ \gamma \cong \gamma' $ ) e adiacenti al lato congruente ( $ BC \cong B'C' $ ) e si può applicare il secondo criterio di congruenza (ALA) dei triangoli.
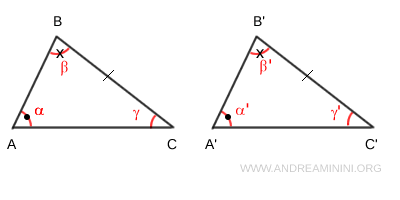
- In un triangolo rettangolo gli angoli acuti sono angoli complementari
E così via.
