Il teorema di Talete

Quando un fascio di rette parallele interseca due trasversali r e s, i segmenti corrispondenti su queste trasversali sono direttamente proporzionali.  $$ AB:CD = A'B':C'D' $$

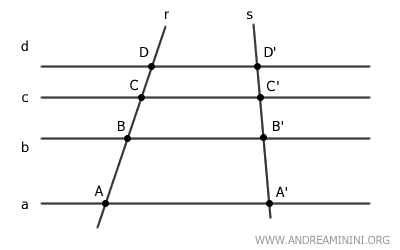
Ad esempio, se ho due segmenti AB e CD sulla trasversale r, allora esistono due segmenti corrispondenti A'B' e C'D' sull'altra trasversale s che hanno la stessa proporzione, ovvero tali che AB sta a CD come A'B' sta a C'D'

$$ AB:CD = A'B':C'D' $$

Quest'ultima formula esprime la relazione di proporzionalità diretta tra le due coppie di segmenti.

Vale anche il teorema inverso di Talete.

Se per ogni coppia di segmenti AB e CD sulla trasversale r esiste una coppia corrispondente di segmenti A'B' e C'D' sull'altra trasversale s tali che la proporzione AB:CD=A'B':C'D' è soddisfatta, allora il fascio di rette che le interseca è un fascio di rette parallele.

Il teorema di Talete e la sua forma inversa stabiliscono le condizioni necessarie e sufficienti perché due o più rette siano tra loro parallele (parallelismo tra due rette) in base alla relazione della proporzionalità diretta.

Il teorema di Talete (o corrispondenza di Talete) è un principio fondamentale della geometria piana. Va detto che la scoperta del teorema è tradizionalmente attribuita a Talete di Mileto, un matematico e filosofo greco antico, anche se è molto probabile che il concetto fosse già noto prima di lui.

Un esempio pratico

Considero un fascio di rette parallele che interseca due rette trasversali r e s in vari punti corrispondenti.

In questo caso tra i segmenti corrispondenti AB e CD sulla retta r e i segmenti corrispondenti A'B' e C'D' sulla retta s, si verifica la seguente proporzione diretta:

$$ AB:CD = A'B':C'D' $$

In altre parole, il segmento AB sta al segmento CD come il segmento A'B' sta al segmento C'D'.

I due segmenti sulle rette trasversali sono direttamente proporzionali.

Il teorema inverso di Talete

Se due coppie di segmenti AB e CD su una retta r e due coppie di segmenti A'B' e C'D' su una retta s sono direttamente proporzionali $$ AB:CD = A'B':C'D' $$ e i segmenti AA' e BB' sono paralleli, allora anche i segmenti CC' e DD' sono paralleli.

In altre parole, se ho due segmenti su una retta e altri due su un'altra retta, e il rapporto tra le lunghezze dei segmenti è lo stesso per entrambe le rette, allora se le linee che collegano gli estremi di una coppia di segmenti sono parallele, anche le linee che collegano gli estremi dell'altra coppia saranno parallele.

Esempio

Ad esempio, considero i segmenti AB e CD sulla retta r e i segmenti A'B' e C'D' sulla retta s

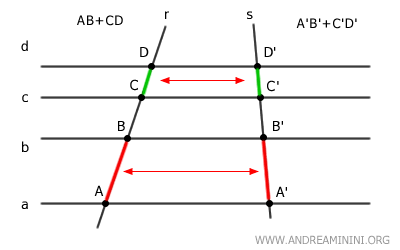
Il rapporto tra le due lunghezze è lo stesso

$$ AB:CD = A'B':C'D' $$

Inoltre, i segmenti che uniscono gli estremi della prima coppia di segmenti sono paralleli.

$$ AA' \ || \ BB' $$

In base al teorema inverso di Talete, se tutte queste condizioni si verificano, allora devono essere paralleli anche i segmenti che collegano gli estremi della seconda coppia.

$$ CC' \ || \ DD' $$

La dimostrazione

Per ipotesi iniziale considero un fascio di rette a, b, c, d parallele tra loro.

$$ a \ || \ b \ || \ c \ || \ d $$

Considero anche due rette trasversali r e s che intersecano il fascio di rette

 

Devo dimostrare la tesi in base al quale, presi due segmenti AB e CD sulla trasversale r, esistono due segmenti A'B' e C'D' sulla trasversale s direttamente proporzionali

$$ AB:CD = A'B':C'D' $$

Indico con R l'insieme di tutti i segmenti sulla trasversale r e con S l'insieme dei segmenti sulla trasversale s.

$$ R = \{ \ \text{segmenti di r} \ \} $$

$$ S = \{ \ \text{segmenti di s} \ \} $$

In base al principio fondamentale della geometria, ogni punto su una retta trasversale r che interseca un fascio di rette parallele corrisponde esattamente a un punto su un'altra trasversale s che interseca lo stesso fascio di rette.

In altre parole, ogni punto sulla trasversale r è associato esattamente a un punto sulla trasversale s.

Ad esempio, al punto A corrisponde il punto A', al punto B corrisponde il punto B', ecc.

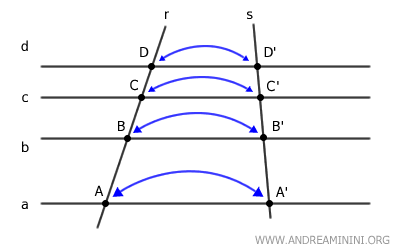
Se esiste una corrispondenza uno-a-uno tra i punti delle rette trasversali r e s, allora esiste anche una corrispondenza biunivoca tra i segmenti delle trasversali r e s.

Ad esempio, il segmento AB corrisponde a A'B', il segmento BC corrisponde a B'C, ecc. 

Da questo deduco l'esistenza di una corrispondenza biunivoca tra gli elementi degli insiemi R e S, ovvero per ogni segmento sulla trasversale r esiste uno e un solo segmento sulla trasversale s.

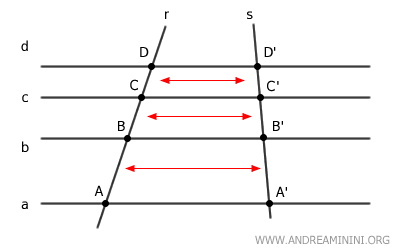
Nota. In sostanza, la corrispondenza uno-a-uno dei segmenti si basa sul fatto che ogni punto di intersezione su una trasversale ha un corrispondente diretto sull'altra trasversale, a causa della natura delle rette parallele che le intersecano.

Secondo il criterio della proporzionalità diretta, due grandezze sono direttamente proporzionali se sono soddisfatte queste condizioni

1. Per ogni coppia di segmenti congruenti sulla trasversale r esiste una coppia di segmenti congruenti sulla trasversale s.
   
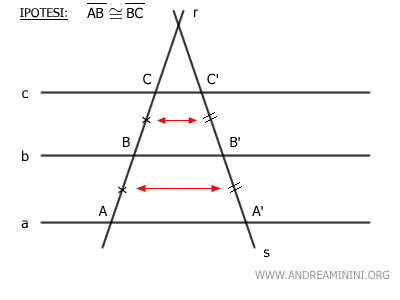
2. Alla somma di due segmenti AB+CD sulla trasversale r corrisponde la somma dei segmenti corrispondenti A'B'+C'D' sulla trasversale s.
   

Queste due condizioni sono soddisfatte grazie alla corrispondenza biunivoca tra i segmenti delle trasversali r e s.

Pertanto, i segmenti corrispondenti sulle trasversali sono direttamente proporzionali.

Osservazioni

Alcune osservazioni, corollari e note a margine sul teorema di Talete

• Teorema della retta parallela a un lato del triangolo
  Se una retta è parallela a un lato del triangolo e interseca gli altri due lati, allora divide questi ultimi in due coppie di segmenti direttamenti proporzionali e viceversa. E' un corollario del teorema di Talete.

  Esempio. La retta r è parallela al lato AB del triangolo e interseca gli altri due lati AC e BC.
  
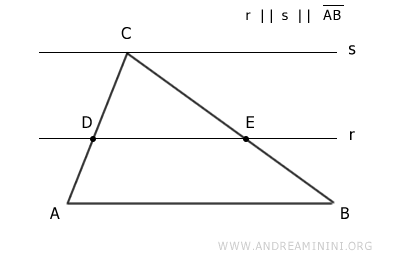
  Secondo il Teorema di Talete il rapporto tra i segmenti AD/DC e BE/EC è lo stesso. $$ \overline{AD} : \overline{DC} = \overline{BE} : \overline{EC} $$ Quindi, i segmenti AD/DC e  BE/EC sono direttamente proporzionali.

• Il teorema della bisettrice
  La bisettrice di un angolo del triangolo taglia il lato opposto in due segmenti direttamente proporzionali agli altri due lati del triangolo. $$ \overline{BD} : \overline{CD} = \overline{AB} : \overline{AC} $$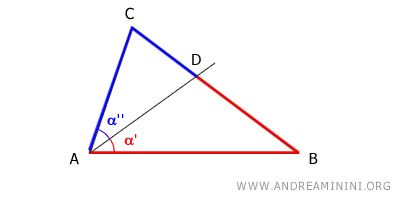

E così via.