Il teorema di Pitagora
Il teorema di Pitagora si applica ai triangoli rettangoli, cioè ai triangoli che hanno un angolo di 90 gradi. L'enunciato del teorema è il seguente:
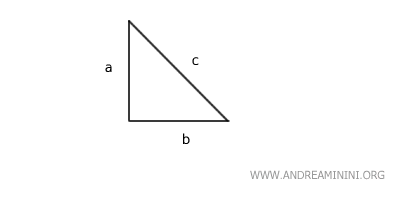
In un triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma delle aree dei quadrati costruiti sugli altri due lati. $$ a^2 + b^2 = c^2 $$ Dove "c" è l'ipotenusa mentre "a" e "b" sono gli altri due lati detti "cateti".
Il teorema prende il nome dal matematico greco Pitagora che, per tradizione, fu il primo ad elaborarlo.
A cosa serve?
Fornisce un modo per calcolare le lunghezze in un triangolo rettangolo.
Ad esempio, conoscendo le misure di due lati del triangolo rettangolo, mi permette di determinare la misura del lato mancante.
Applicazioni del Teorema. Il teorema di Pitagora ha una vasta gamma di applicazioni in vari campi della matematica, della geometria e della fisica. Ad esempio, è usato per calcolare le distanze tra punti nello spazio. In trigonometria, è alla base delle definizioni delle funzioni seno, coseno e tangente.
Nonostante sia un teorema formulato migliaia di anni fa, è ancora oggi un elemento importante della scienza moderna, perché è presente in moltissime dimostrazioni di altri concetti e teoremi di geometria, matematica e fisica.
Un esempio pratico
Considero un triangolo rettangolo.
I due lati adiacenti all'angolo retto misurano 4 e 3.
$$ a=4 \\ b=3 $$
Non conosco però la lunghezza del lato opposto all'angolo retto ossia dell'ipotenusa (lato c).
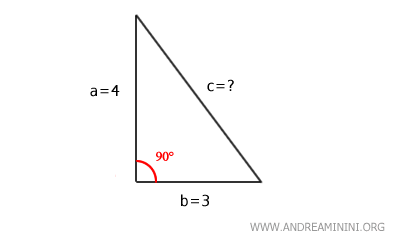
Le misure dei due lati adiacenti mi permettono di calcolare la lunghezza del lato opposto all'angolo retto, usando il teorema di Pitagora.
Il quadrato dell'ipotenusa (c2) è uguale alla somma dei quadrati costruiti sui cateti (a2+b2).
$$ c^2 = a^2 + b^2 $$
Sapendo che le misure note dei lati sono a=4 e b=3, sostituisco i valori.
$$ c^2 = 4^2 + 3^2 $$
$$ c^2 = 16 + 9 $$
$$ c^2 = 25 $$
A questo punto, applico la proprietà invariantiva delle equazioni e calcolo la radice quadrata in entrambi i membri.
$$ \sqrt{c^2} = \sqrt{25} $$
$$ c = 5 $$
Ho così trovato la lunghezza dell'ipotenusa c=5.
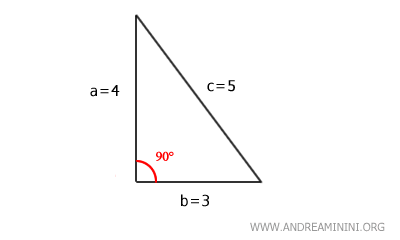
Allo stesso modo conoscendo un cateto e l'ipotenusa, posso ricavare la misura dell'altro cateto. $$ a^2 = c^2 - b^2 $$ $$ b^2 = c^2 - a^2 $$ Per ricordare tutte le formule basta ricordarsi la formula principale del teorema di Pitagora, ossia c2=a2+b2, e poi spostare il lato di cui non si conosce la lunghezza su un membro dell'equazione e gli altri due lati noti sull'altro membro dell'equazione.
La dimostrazione
Esistono molte dimostrazioni del teorema di Pitagora, alcune delle quali risalgono a migliaia di anni fa.
Una delle dimostrazioni più semplici e famose utilizza un approccio geometrico.
Considero un triangolo rettangolo.
Sui tre lati del triangolo rettangolo, disegno tre quadrati.
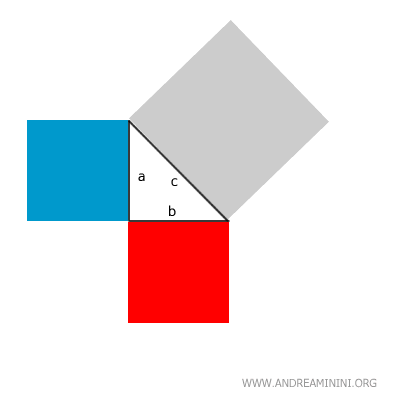
Il quadrato più grande (grigio) è costruito sull'ipotenusa, il lato più lungo del triangolo, mentre gli altri due quadrati (rosso e blu) sono costruiti sui lati più corti ossia sui cateti.
Divido ciascun quadrato piccolo in due triangoli rettangoli.
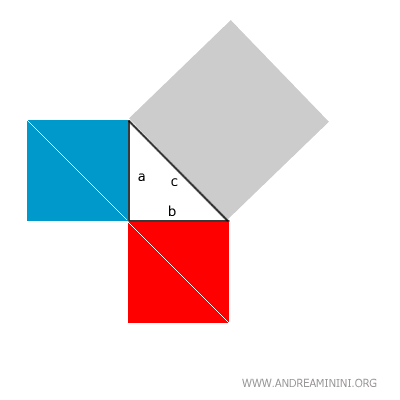
Quindi, riorganizzo i pezzi in modo da coprire esattamente l'area del quadrato più grande.
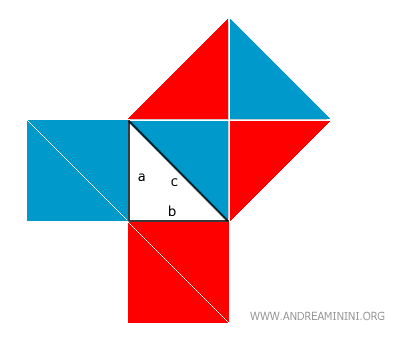
Questo dimostra che l'area del grande quadrato è uguale alla somma delle aree dei due quadrati più piccoli, dimostrando così il teorema.
Dimostrazione alternativa
Un altro modo per dimostrare il teorema di Pitagora utilizza il teorerema di Euclide.
Per prima cosa costruisco i quadrati sui cateti e sull'ipotenusa.
Traccio l'altezza (h) del triangolo considerando l'ipotenusa (c) come base.
L'altezza è la proiezione dei cateti sull'ipotenusa tramite una retta perpendicolare.
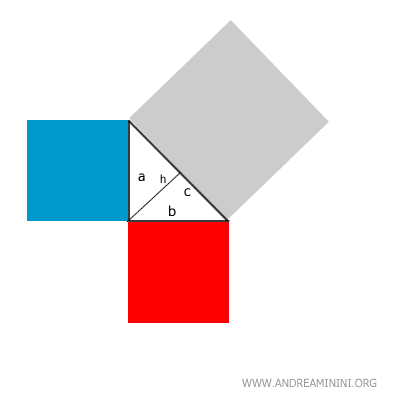
Prolungo l'altezza in modo da tagliare in due parti il quadrato costruito sull'ipotenusa.
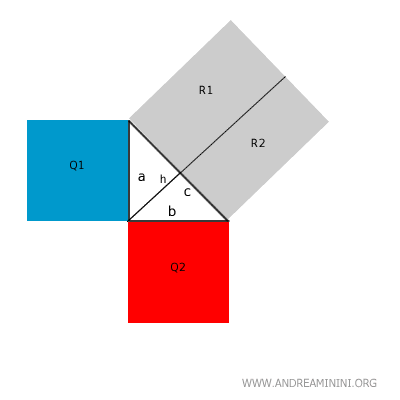
La superficie del quadrato costruito sull'ipotenusa è la somma delle aree R1+R2.
In base al primo teorema di Euclide, il rettangolo costruito utilizzando la proiezione del cateto "a" sull'ipotenusa ha la stessa area del quadrato sul cateto "a" ossia Q1=R1.
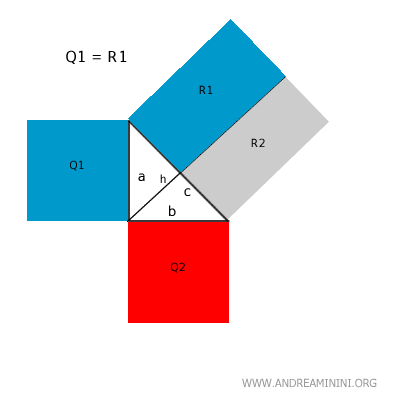
Per la stessa ragione (primo teorema di Euclide) anche il rettangolo costruito tramite la proiezione del cateto "b" ha la stessa area del quadrato sul cateto "b" ossia Q2=R2.
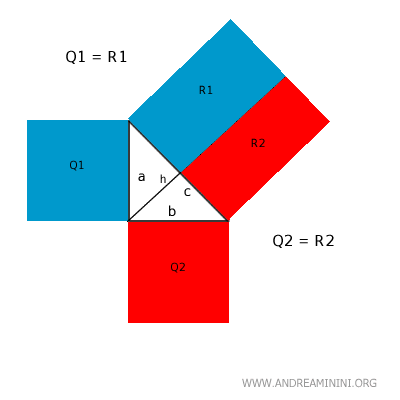
Sapendo che il quadrato costruito sull'ipotenusa è la somma dei due rettangoli R1+R2 e che R1=Q1 e R2=Q2, deduco che il quadrato dell'ipotenusa è uguale alla somma dei quadrati dei cateti.
$$ R1+R2 \doteq Q1+Q2 $$
Questo dimostra il teorema di Pitagora.
Nota. Esistono moltissime altre dimostrazioni del teorema di Pitagora. Queste sono solo due dimostrazioni tra tante. Ne esistono centinaia.
Osservazioni
Alcune osservazioni e note aggiuntive sul teorema di Pitagora
- L'inverso del teorema di Pitagora
Se in un triangolo la somma dei quadrati costruiti su due lati è equivalente (stessa area) al quadrato costruito sul terzo lato restante, allora il triangolo è un triangolo rettangolo.
- Il teorema di Pitagora generalizzato o esteso
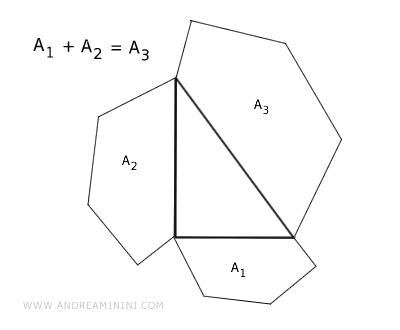
In un triangolo rettangolo, se costruisco tre poligoni simili sui tre lati del triangolo, allora l'area del poligono costruito sull'ipotenusa (A3) è uguale alla somma delle aree (A1+A2) dei due poligoni costruiti sui cateti.
- L'origine del teorema di Pitagora
Una leggenda narra che Pitagora abbia formulato il suo teorema mentre aspettava un'udienza dal tiranno Policrate nel palazzo di Samo, osservando le piastrelle quadrate del pavimento della sala d'attesa. Una piastrella era rotta in diagonale, formando due triangoli isosceli. Pitagora immaginò di costruire un quadrato sulla diagonale della mezza piastrella e notò che la sua superficie era perfettamente uguale alla somma delle aree dei quadrati costruiti sugli altri due lati del triangolo rettangolo. Questo dimostra anche che le grandi intuizioni, spesso derivano da piccoli fatti sotto gli occhi di tutti. Una piastrella rotta o una mela che cade da un albero.
E così via.
