Il terzo criterio di congruenza dei triangoli
Due triangoli sono congruenti se hanno tutti i lati congruenti nello stesso ordine.
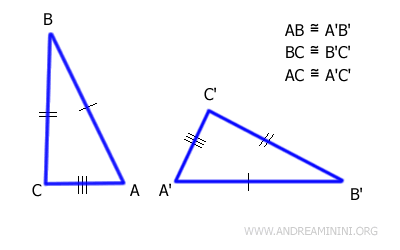
In altre parole, due triangoli sono considerati congruenti quando tutti i loro lati corrispondono in lunghezza nella stessa sequenza.
Questo criterio è noto anche come LLL (Lato-Lato-Lato)
Ad esempio, considero due triangoli ABC e A'B'C'
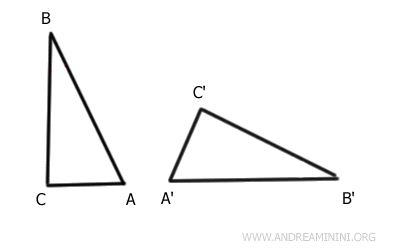
Dopo un movimento rigido (traslazione+rotazione) il lato AB del primo triangolo è sovrapponibile punto a punto al lato A'B' del secondo triangolo.
Quindi, i lati AB e A'B' hanno la stessa lunghezza ossia sono congruenti.
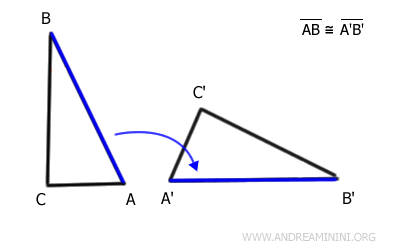
Ora considero i segmenti successivi ad AB e A'B' ossia BC e B'C'
Dopo un'altra trasformazione rigida, che comprende traslazione e rotazione, il segmento BC del primo triangolo coincide perfettamente con il segmento B'C' del secondo triangolo.
Pertanto, i segmenti BC e B'C' presentano la stessa misura e sono, di conseguenza, congruenti.
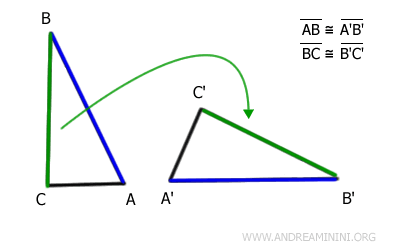
Infine, prendo in considerazione i segmenti successivi ad BC e B'C', ovvero AC e A'C'.
A seguito di un'ulteriore trasformazione rigida, che combina traslazione e rotazione, il segmento AC del primo triangolo si sovrappone esattamente al segmento A'C' del secondo triangolo.
Di conseguenza, i segmenti AC e A'C' hanno la stessa lunghezza e sono pertanto congruenti.
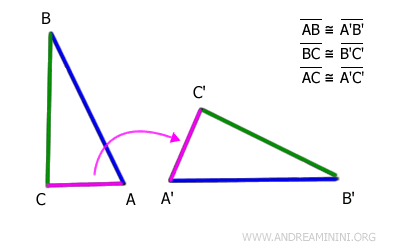
Tutti i segmenti dei due triangoli sono congruenti tra loro nello stesso ordine.
Pertanto, i due triangoli sono congruenti.
La dimostrazione
Anche in questo caso su tratta di un teorema perché è dimostrabile.
Considero i due triangoli ABC e A'B'C' già visti nell'esempio precedente.

I due triangoli hanno tutti i lati congruenti nello stesso ordine.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
Devo dimostrare i due triangoli ABC e A'B'C' siano effettivamente congruenti.
Con un movimento rigido (traslazione+rotazione+riflessione) faccio coincidere i lati AB=A'B' dei due triangoli
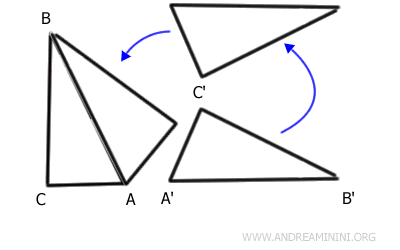
Al nuovo vertice associo l'etichetta C''
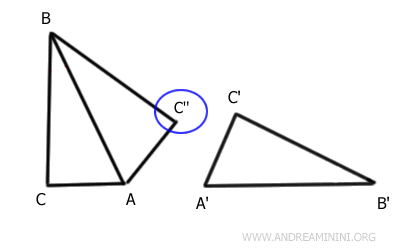
Pertanto, i triangoli AC''B e A'B'C' sono congruenti.
$$ AC''B \cong A'B'C' $$
Traccio un segmento che unisce i punti C e C''.
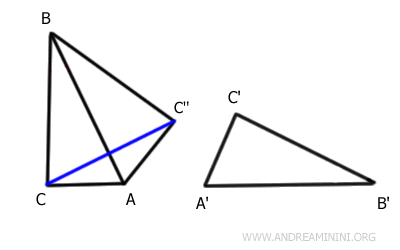
Il triangolo AC''C è un triangolo isoscele alla base CC'' perché AC≅A'C'≅AC''
Sapendo che gli angoli alla base di un triangolo isoscele sono congruenti, deduco che gli angoli nei vertici C e C'' sono congruenti
$$ A \hat{C} C \text{''} \cong A \hat{C} \text{''} C $$
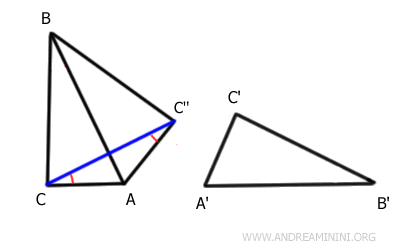
Anche il triangolo CBC'' è un trangolo isoscele alla base CC'' perché BC≅B'C'≅BC''
Tenendo conto che in un triangolo isoscele gli angoli alla base sono congruenti, posso affermare che gli angoli situati nei vertici C e C'' sono effettivamente congruenti.
$$ B \hat{C} C \text{''} \cong B \hat{C} \text{''} C $$
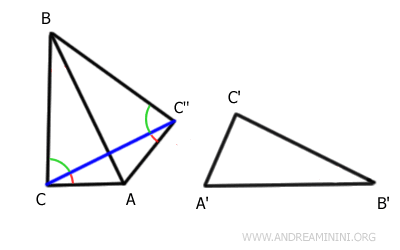
Le somme di due coppie di angoli congruenti sono a loro volta congruenti
$$ A \hat{C} C \text{''} + B \hat{C} C \text{''} \cong B \hat{C} \text{''} C + A \hat{C} \text{''} C $$
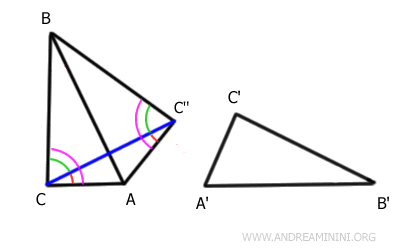
Pertanto, gli angoli (di colore viola) nei vertici C e C'' sono congruenti.
$$ A \hat{C} B \cong A \hat{C} \text{''} B $$
A questo punto sapendo che il triangolo ACC'' è isoscele alla base CC'', deduco che i lati AC e AC'' sono congruenti
$$ \overline{AC} \cong \overline{AC} \text{''} $$
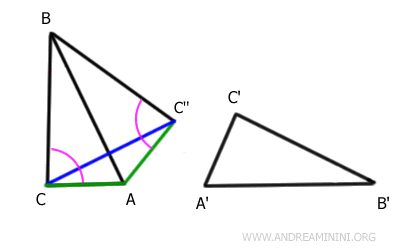
Sapendo che anche il triangolo BCC'' è isoscele alla base CC'', deduco che i lati BC e BC'' sono congruenti
$$ \overline{BC} \cong \overline{BC} \text{''} $$
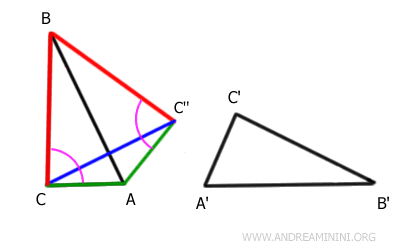
Per il primo principio di congruenza i triangoli ABC e ABC'' sono congruenti perché hanno due lati congruenti BC'≅BC'' , AC'≅AC'' e l'angolo tra di essi congruente γ=γ''.
$$ ABC \cong ABC'' $$
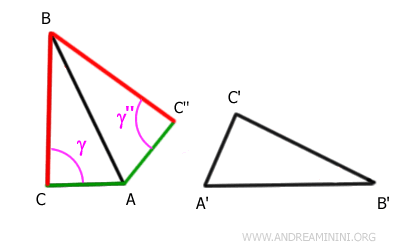
A sua volta che il triangolo ABC'' è congruente con il triangolo A'B'C' per la costruzione iniziale.
$$ ABC'' \cong A'B'C' $$
Quindi, per la proprietà transitiva anche il triangolo ABC è congruente con il triangolo A'B'C'
$$ ABC \cong ABC'' \cong A'B'C' $$
ovvero
$$ ABC \cong A'B'C' $$
E' quello che volevo dimostrare.
Dimostrazione alternativa
Considero due triangoli ABC e A'B'C' con i lati congruenti nello stesso ordine.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
Devo dimostrare la tesi che a partire da queste ipotesi, i due triangoli ABC e A'B'C' sono congruenti.
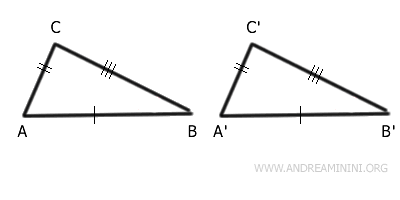
Traccio una semiretta A''B che forma lo stesso angolo $ \beta' $ sul vertice B e ha la stessa lunghezza del lato A'B'.
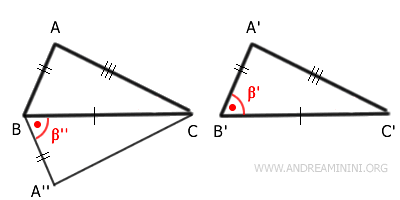
Pertanto, i segmenti $ \overline{A'B'} \cong \overline{A''B} $ e gli angoli $ \beta' \cong \beta'' $ sono congruenti per costruzione.
I triangoli A''BC e A'B'C' hanno un lato congruente per ipotesi $ \overline{BC} \cong \overline{B'C'} $, un lato congruente per costruzione $ \overline{A'B'} \cong \overline{A''B'} $ e l'angolo tra questi è congruente per costruzione $ \beta' \cong \beta'' $.
Quindi, per il primo criterio di congruenza i due triangoli $ A''BC \cong A'B'C' $ sono congruenti.
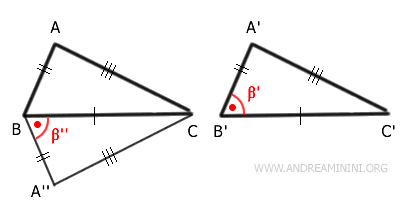
Congiungo con un segmento $ \overline{AA''} i vertici A e A''.
Il triangolo ABA'' è isoscele perché i lati obliqui sono congruenti $ \overline{AB} \cong \overline{A''B} $. Quindi l'angolo $ B\hat{A}A'' \cong B''A $ sono congruenti.
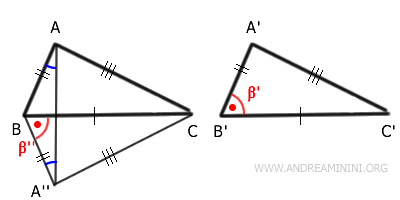
Anche il triangolo $ ACA'' $ è un triangolo isoscele perché i lati obliqui $ \overline{AC} \cong \overline{A''C} $ sono congruenti.
Pertanto, anche gli angoli alla base del triangolo isoscele $ C \hat{A}A'' \cong C \hat{A''}A $ sono congruenti.
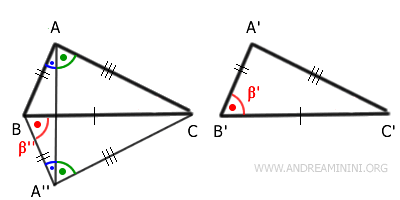
Sono congruenti anche gli angoli $ B \hat{A} C \cong B \hat{A''} C $ ( ossia $ \alpha \cong \alpha'' $ ) in quanto somme di angoli congruenti.
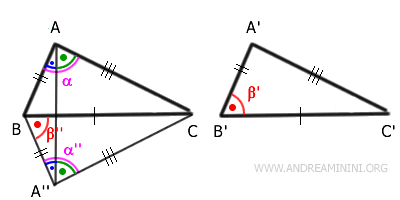
Quindi, per il primo criterio di congruenza anche i triangoli $ ABC \cong A''BC $ sono congruenti, perché hanno due lati congruenti $ AB \cong A''B $ e $ AC \cong A''C $ e l'angolo tra di questi $ \alpha \cong \alpha'' $ è congruente.
$$ ABC \cong A''BC $$
Sapendo che $ A''BC \cong A'B'C' $, per la proprietà transitiva deduco che anche i triangoli $ ABC \cong A'B'C' $ sono congruenti.
$$ ABC \cong A''BC \cong A'B'C' $$
In questo modo la tesi è dimostrata.
E così via.
