Il circocentro
Il circocentro di un triangolo è il punto in cui si incontrano gli assi del triangolo, ossia le rette perpendicolari passanti per il punto medio dei lati del triangolo.
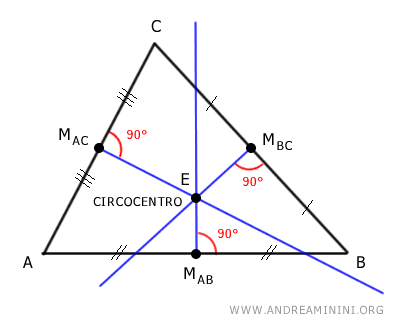
Le rette perpendicolari passanti per il punto medio di ogni lato del triangolo sono anche chiamate assi del triangolo, mediane perpendicolari o bisettrici perpendicolari.
Il circocentro è anche il centro del cerchio circoscritto, detto circocerchio, che passa attraverso tutti e tre i vertici del triangolo.
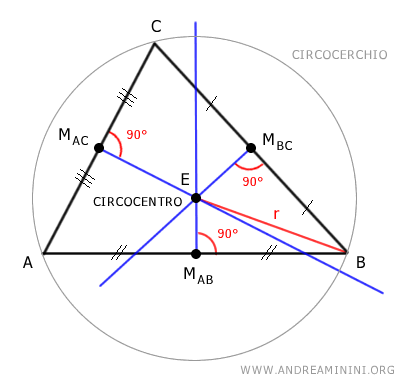
Centro del circocerchio. Il circocentro è il centro del cerchio circoscritto che passa attraverso i vertici del triangolo. Pertanto, il circocentro è equidistante dai tre vertici del triangolo. Questa distanza è detta raggio del circocerchio (r).
Come trovare il circocentro
Considero un triangolo ABC
Il triangolo ha tre vertici A, B, C e tre lati AB, BC e AC.
Individuo il punto medio di ogni lato del triangolo: MAB, MBC e MAC.
Cos'è il punto medio? Il punto medio di un segmento è il punto del segmento che lo divide in due parti congruenti, ossia della stessa lunghezza.
Per ciascun lato del triangolo, traccio la retta perpendicolare passante per il punto medio.
Ogni retta perpendicolare forma un angolo retto (90°) rispetto al lato del triangolo.
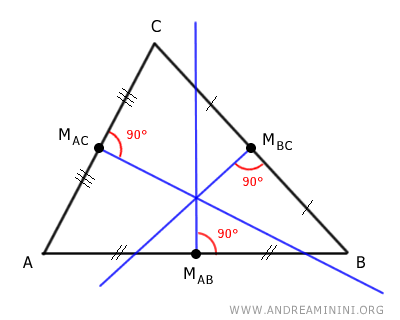
Il punto di intersezione delle tre rette perpendicolari è il circocentro.

A questo punto traccio un segmento r tra il circocentro e uno dei vertici del triangolo. Ad esempio, il vertice B
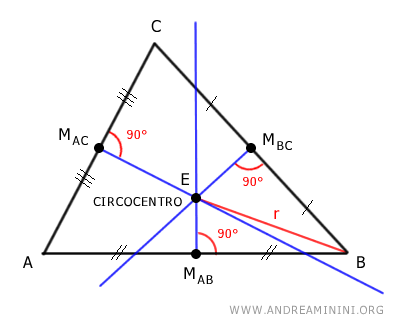
Il segmento r è il raggio di una circonferenza circoscritta passante per tutti i vertici del triangolo, detta circocerchio.

La dimostrazione
La dimostrazione dell'esistenza del circocentro è molto semplice e rapida.
Considero un generico triangolo ABC di qualsiasi forma.
In tre punti distinti e non allineati può passare una e una sola circonferenza.
Quindi, un triangolo è sempre inscrivibile in una circonferenza, perché nei tre vertici di un triangolo passa una e una sola circonferenza che ha per centro il circocentro (O).
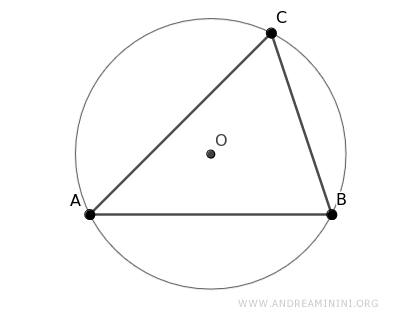
Per costruzione, il lato AB del triangolo è una corda della circonferenza.
Sapendo che l'asse di una corda passa sempre per il centro di una circonferenza, deduco che l'asse del segmento AB passa per il centro della circonferenza O (circocentro).
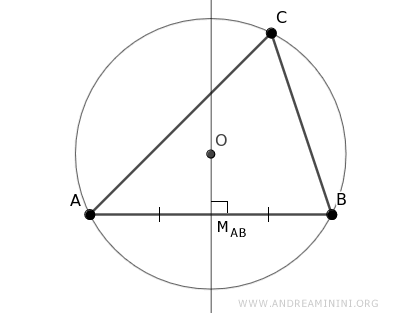
Lo stesso ragionamento posso applicarlo agli altri lati BC e AC perché sono altre due corde della circonferenza.
Traccio le perpendicolari dai punti medi di questi lati (assi dei segmenti) e anche queste passano per il circocentro O.
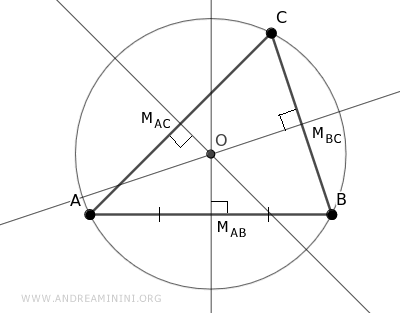
Questo dimostra che il punto di intersezione degli assi del triangolo è il centro della circonferenza che circoscrive il triangolo.
Osservazioni
Alcune osservazioni e caratteristiche del circocentro.
- La posizione del circocentro dipende dal tipo di triangolo
- In un triangolo acutangolo il circocentro si trova all'interno del triangolo.
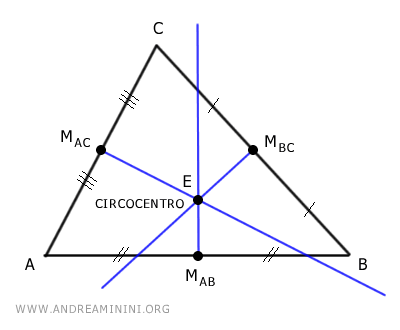
- In un triangolo ottusangolo il circocentro si trova all'esterno del triangolo.
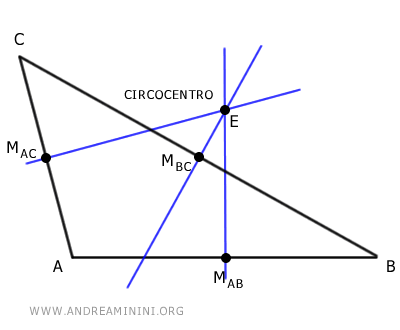
- In un triangolo rettangolo il circocentro si trova sul lato ipotenusa. Nel caso di un triangolo rettangolo, il circocentro coincide con il punto medio dell'ipotenusa (MBC).
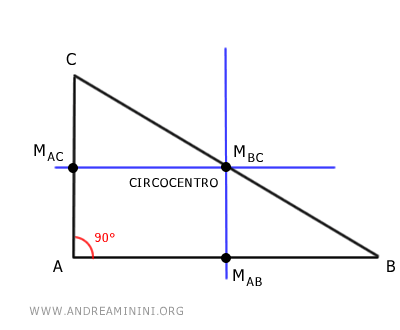
- In un triangolo acutangolo il circocentro si trova all'interno del triangolo.
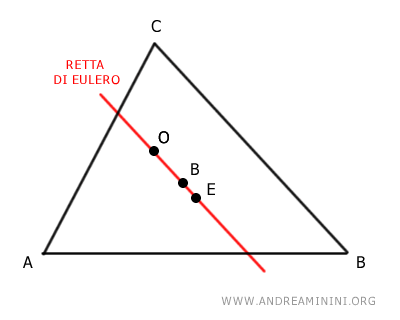
- Il circocentro giace sempre sulla retta di Eulero
La retta di Eulero è la retta passante per il baricentro (B), il circocentro (E) e l'ortocentro (O) di un triangolo.
E così via.
