Teorema della retta parallela al lato di un triangolo
Una retta parallela a un lato di un triangolo interseca gli altri due lati dividendoli in segmenti proporzionali.
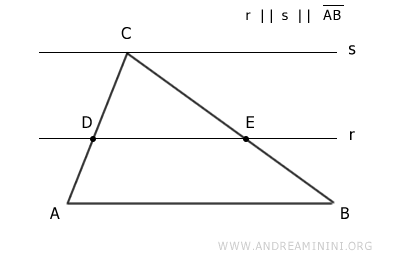
Questo teorema deriva dal teorema di Talete.
Stabilisce che se una retta parallela a un lato di un triangolo interseca gli altri due lati, allora divide questi due lati in segmenti proporzionali.
È una delle basi della similitudine nei triangoli.
Vale anche il teorema inverso
Se una retta interseca due lati del triangolo divididendoli in segmenti proporzionali, allora questa retta è parallela al restante lato del triangolo.
Quindi, questo teorema è anche un criterio di parallelismo nella geometria euclidea. In altre parole, offre un modo per determinare se una retta è parallela a un'altra.
Nota. Questo principio è utilizzato di frequente in problemi di geometria piana per determinare la parallelità delle rette e per risolvere problemi relativi a triangoli simili. Inoltre, può anche essere esteso a concetti più avanzati come la geometria proiettiva e la teoria delle proporzioni.
Un esempio pratico
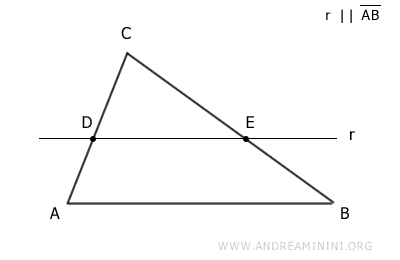
Ad esempio, considero un triangolo ABC.
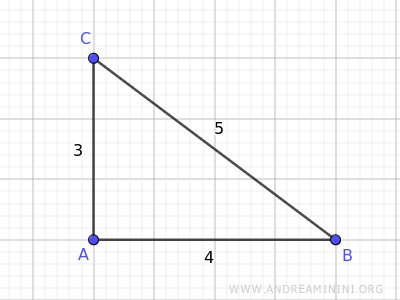
Conosco già le lunghezze dei lati del triangolo AB=4, BC=5, AC=3.
Traccio una retta retta parallela al lato AB che interseca gli altri due lati del triangoli nei punti D e E.
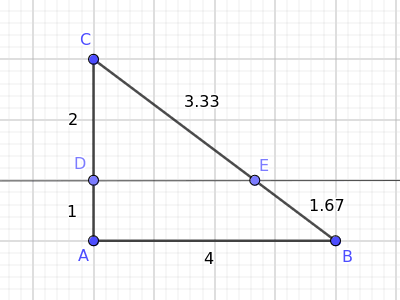
Questa retta interseca i lati AC e BC in due punti, D ed E rispettivamente.
- Il segmento AC viene suddiviso in due segmenti AD e DC lunghi rispettivamente 1 e 2.
- Il segmento BC viene suddiviso in due segmenti BE e EC lunghi rispettivamente 1.67 e 3.33
Il Teorema di Talete afferma che AD/DC = BE/EC, ovvero che le due coppie di segmenti sono direttamente proporzionali.
$$ \frac{ \overline{AD} }{ \overline{DB} } = \frac{ \overline{BE} }{ \overline{EC} } $$
Sostituisco i valori dei segmenti AD=1, DC=2, BE=1.67, EC=3.33
$$ \frac{ 1 }{ 2 } = \frac{ 1.6\overline{7} }{ 3.\overline{33} } $$
$$ 0.5 = 0.5 $$
Il rapporto tra i segmenti AD/DC e BE/EC è lo stesso.
Quindi, le due coppie di segmenti sono direttamente proporzionali.
La dimostrazione
La dimostrazione del teorema è molto semplice.
Considero un triangolo ABC qualsiasi.
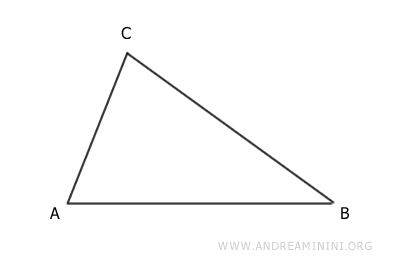
Per ipotesi iniziale traccio una retta parallela r a un lato AB del triangolo che interseca gli altri due lati nei punti D e E.
Poi aggiungo un ulteriore retta s passante per il vertice opposto al lato AB del triangolo.

Il segmento AB e le rette parallele r,s formano un fascio di rette tagliate dalle due trasversali BC e AC.
Secondo il teorema di Talete i due lati BC e AC sono suddivisi in modo proporzionale.
$$ AD:DC = BE:EC $$
Pertanto, i due lati sono divisi in modo direttamente proporzionale.
Dimostrazione del teorema inverso
Poiché il teorema di Talete ammette anche il teorema inverso, posso dedurre che vale lo stesso anche per il suo corollario.
Se per ipotesi una retta divide due lati del triangolo in segmenti direttamente proporzionali, allora deduco che questa retta è parallela al restante lato del triangolo.
E così via.
