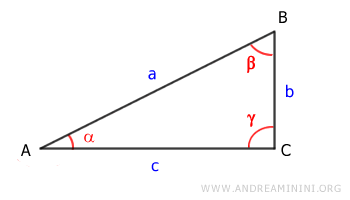
Secondo teorema del triangolo rettangolo
- In un triangolo rettangolo la lunghezza di un cateto è uguale
- al prodotto tra la tangente dell'angolo opposto per l'altro cateto $$ b = c \cdot \tan \alpha $$
- al prodotto tra la cotangente dell'angolo adiacente per l'altro cateto $$ b = c \cdot \ cotg \ \beta $$
Allo stesso modo l'altro cateto (c) è uguale al prodotto della tangente dell'angolo opposto per l'altro cateto
$$ c = b \cdot \tan \beta $$
e al prodotto della cotangente dell'angolo adiacente per l'altro cateto
$$ c = b \cdot \ cotg \ \alpha $$
Un esempio pratico
Considero un triangolo rettangolo
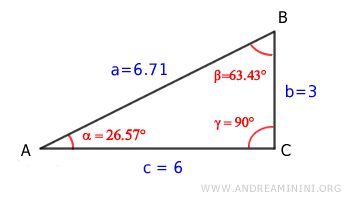
La lunghezza dell'ipotenusa è
$$ a = \overline{AB} = 6.71 $$
La lunghezza dei due cateti è
$$ b = \overline{BC} = 3 $$
$$ c = \overline{AC} = 6 $$
Gli angoli del triangolo rettangolo sono
$$ \alpha = 26.57° $$
$$ \beta = 63.43° $$
$$ \gamma = 90° $$
Per ottenere la lunghezza del cateto b moltiplico la tangente dell'angolo opposto (α) per l'altro cateto (c)
$$ b = c \cdot \tan \alpha = 6 \cdot \tan ( 26.57° ) = 3 $$
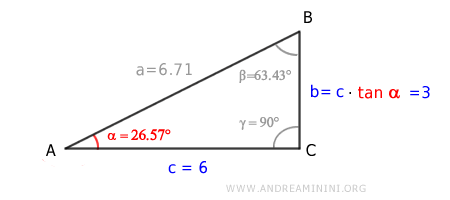
In alternativa, per avere la lunghezza del cateto b moltiplico la cotangente dell'angolo adiacente (β) per l'altro cateto (c)
$$ b = c \cdot \ cotg \ \beta = 6 \cdot \ cotg \ ( 63.43° ) = 3 $$
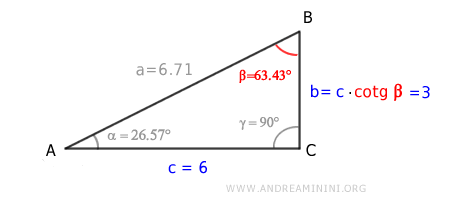
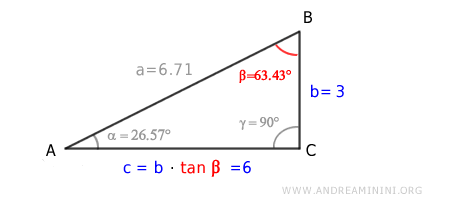
Per ottenere la lunghezza del cateto c moltiplico la tangente dell'angolo opposto (β) per l'altro cateto (b)
$$ c = b \cdot \tan \beta = 3 \cdot \tan ( 63.43° ) = 6 $$
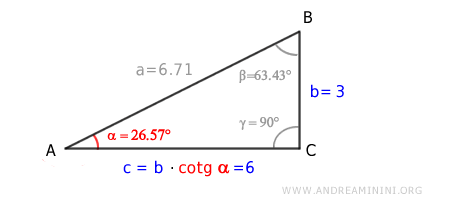
In alternativa, per avere la lunghezza del cateto b moltiplico la cotangente dell'angolo adiacente (α) per l'altro cateto (b)
$$ c = b \cdot \ cotg \ \alpha = 3 \cdot \ cotg \ ( 26.57° ) = 6 $$
La dimostrazione
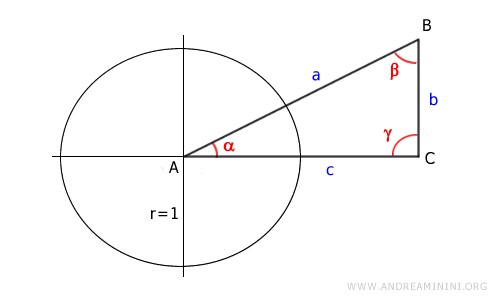
Disegno un triangolo rettangolo ABC. L'angolo retto è l'angolo γ.

Traccio sul rettangolo la circonferenza goniometrica con centro sul vertice A del rettangolo.
Chiamo D il punto di intersezione tra l'ipotenusa (AB) del triangolo rettangolo e la circonferenza goniometrica.
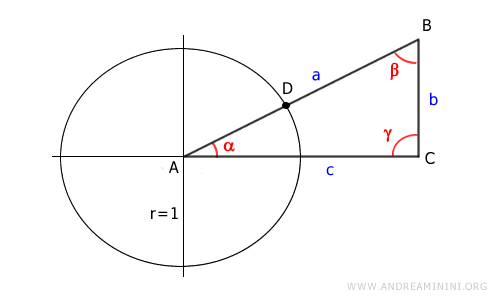
Proietto il punto D sul cateto AC del rettangolo individuando il punto E.
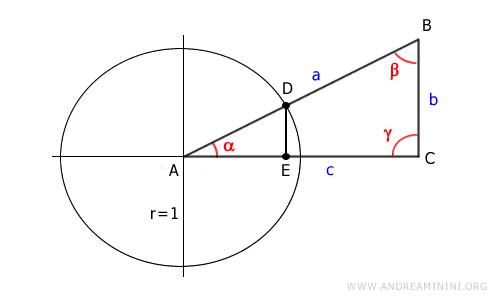
Così facendo ottengo un altro triangolo rettangolo ADE dentro la circonferenza goniometrica.
I triangoli ABC e ADE sono triangoli simili in quanto sono entrambi triangoli rettangoli e hanno l'angolo acuto α in comune.
Pertanto, posso scrivere la seguente proporzione
$$ \overline{BC} : \overline{AC} = \overline{DE} : \overline{AE} $$
Riscrivo la proporzione come uguaglianza tra frazioni
$$ \frac{ \overline{BC} }{ \overline{AC} } = \frac{ \overline{DE} }{ \overline{AE} } $$
Sapendo che BC è il lato b e AC è il lato c
$$ \frac{ b }{ c } = \frac{ \overline{DE} }{ \overline{AE} } $$
Il lato DE è il seno dell'angolo alfa (α)
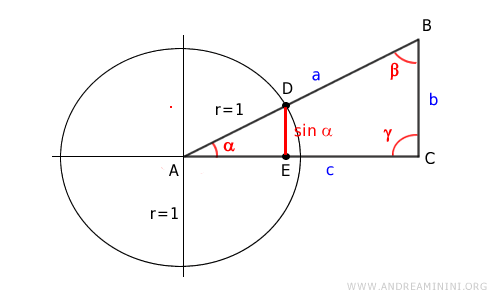
Pertanto, posso sostituire il lato DE con sin α
$$ \frac{ b }{ c } = \frac{ \sin \alpha }{ \overline{AE} } $$
Il lato AE è il coseno dell'angolo alfa (α)
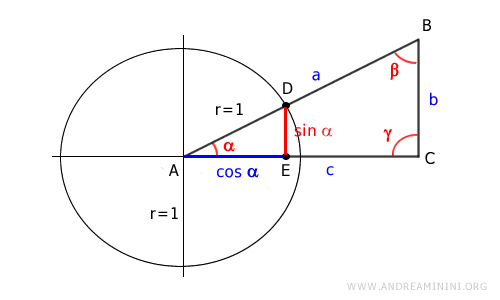
Pertanto, posso sostituire il lato AE con cos α
$$ \frac{ b }{ c } = \frac{ \sin \alpha }{ \cos \alpha } $$
Metto in evidenza il cateto b
$$ b = c \cdot \frac{ \sin \alpha }{ \cos \alpha } $$
In base al secondo teorema fondamentale della trigonometria il rapporto tra il seno e coseno di un angolo è uguale alla tangente dell'angolo ossia sin(α)/cos(α)=tan(α)
$$ b = c \cdot \tan \alpha $$
Pertanto, il cateto b è uguale al prodotto tra la tangente dell'angolo opposto (α) e l'altro cateto (c).

Sapendo che la cotangente è l'inverso della tangente ctg = 1/tan allora tan = 1/cotg
$$ b = c \cdot \frac{1}{cotg \ \alpha} $$
Metto in evidenza il cateto c
$$ c = b \cdot \ cotg \ alpha $$
Pertanto, il cateto c è uguale al prodotto tra la cotangente dell'angolo adiacente (α) per l'altro cateto.
In questo modo ho dimostrato il teorema iniziale, un cateto del triangolo rettangolo è uguale al prodotto tra la tangente dell'angolo opposto per l'altro cateto e al prodotto tra la cotangente dell'angolo adiacente per l'altro cateto.
E così via.
