Parallelogramma
Un parallelogramma è una figura geometrica piana a quattro lati (un quadrilatero) in cui i lati opposti sono paralleli e uguali in lunghezza (congruenti).
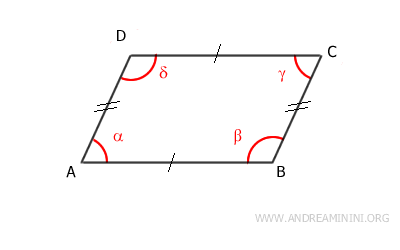
Ecco alcune proprietà comuni dei parallelogrammi
- I lati opposti sono paralleli e congruenti
- Gli angoli opposti sono congruenti, hanno la stessa ampiezza.
- Gli angoli adiacenti a un lato sono supplementari, la loro somma è 180°.
- Le diagonali si incontrano nel loro punto medio.
- Ogni diagonale divide il parallelogramma in due triangoli congruenti.
Alcuni esempi comuni di parallelogrammi sono il rettangolo e il rombo, che rappresentano dei casi particolari con ulteriori proprietà.
Il parallelogramma è una figura geometrica convessa, perché può essere vista come l'intersezione di due strisce non parallele.
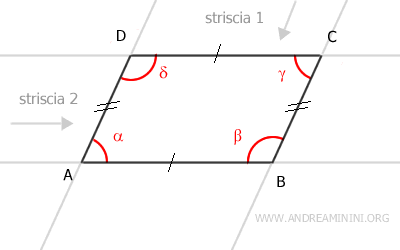
Dove la "striscia" è la parte del piano compresa tra due rette parallele.
Le principali formule dei parallelogramma
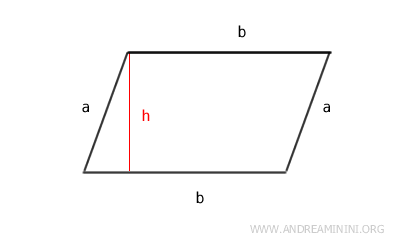
- Il perimetro del parallelogramma è uguale a due volte la somma della base (b) e del lato obliquo (a). $$ P = 2 \cdot (a+b) $$
- L'area del parallelogramma è il prodotto della base (b) per l'altezza (h) $$ A = b \cdot h $$
La base e l'altezza del parallelogramma
In un parallelogramma ogni lato può essere considerato come base (b) e uno dei suoi due lati consecutivi come altezza (h).
L'altezza (h) è la distanza fra il lato opposto alla base e la retta che contiene la base.
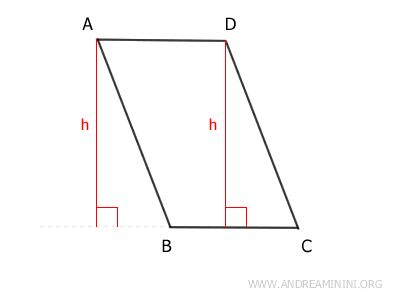
Ad esempio, il segmento h è l'altezza del parallelogramma ABCD se scelgo il lato AB come base.
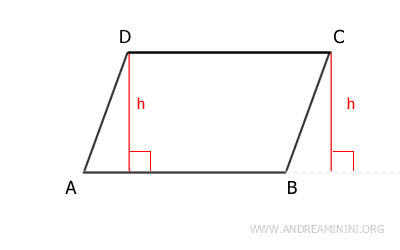
Viceversa, se scelgo il lato BC come base, le altezze (h) del parallelogramma sono le seguenti:
Tipi di parallelogrammi
Nell'insieme dei parallelogrammi fanno parte diverse figure geometriche comuni, come i rettangoli, i rombi e i quadrati.
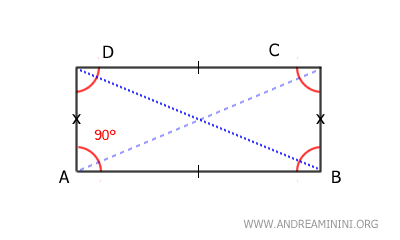
- Rettangoli
I rettangoli sono tipi di parallelogrammi caratterizzati da angoli che misurano 90°.
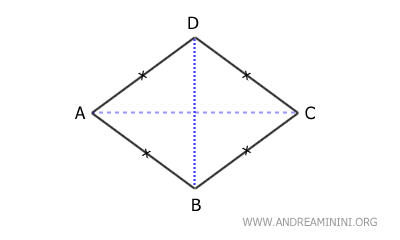
- Rombi
I rombi sono parallelogrammi dove ogni lato ha la stessa lunghezza e le loro diagonali sono mutualmente perpendicolari.
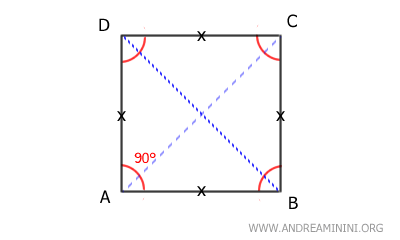
- Quadrati
I quadrati sono parallelogrammi speciali che combinano le proprietà dei rettangoli e dei rombi. Hanno angoli di 90°, lati di lunghezza uniforme e diagonali che si intersecano perpendicolarmente.
Quindi, rettangoli, rombi e quadrati sono casi particolari di parallelogrammi.
In questa tabella sono riassunte le principali differenze.
| Proprietà | Parallelogramma | Rettangolo | Rombo | Quadrato |
|---|---|---|---|---|
| Lati opposti congruenti | SI | SI | SI | SI |
| Angoli opposti congruenti | SI | SI | SI | SI |
| Angoli adiacenti a ciascun lato supplementari | SI | SI | SI | SI |
| Diagonali si incontrano nel loro punto medio | SI | SI | SI | SI |
| Ogni diagonale divide in due triangoli congruenti | SI | SI | SI | SI |
| Le diagonali sono congruenti | -- | SI | -- | SI |
| Le diagonali sono perpendicolari fra loro | -- | -- | SI | SI |
| Le diagonali sono bisettrici degli angoli | -- | -- | SI | SI |
| I lati sono tutti congruenti | -- | -- | SI | SI |
| La somma degli angoli interni è 360° | SI | SI | SI | SI |
Il teorema del parallelogramma
Un quadrilatero convesso è un parallelogramma se soddisfa una delle seguenti condizioni
- I lati opposti sono congruenti
- Gli angoli opposti sono congruenti
- Le diagonali si incontrano nel loro punto medio
- I due lati opposti sono congruenti e paralleli

Se una delle condizioni è soddisfatta lo sono anche le altre.
Quindi, è sufficiente controllare che almeno una delle condizioni sia soddisfatta per stabilire se un quadrilatero è un parallelogramma oppure no.
Come costruire un parallelogramma
Per prima cosa traccio due lati consecutivi del parallelogramma.
Disegno il lato lungo AB seguito dal lato corto BC (o viceversa).
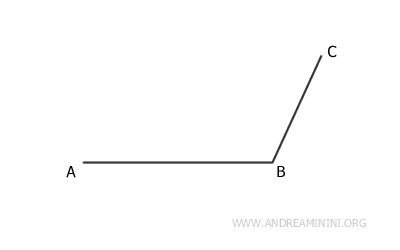
Centro il compasso sul vertice A e con raggio BC traccio un primo arco.
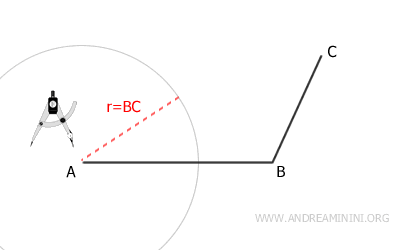
Centro il compasso sul vertice C e con raggio AB traccio un secondo arco.
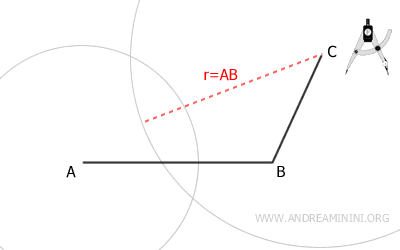
I due archi possono intersecarsi in due punti distinti del piano: D e E.
Tuttavia, solo in uno dei due si ottiene un poligono convesso (D). Quindi, l'altro punto (E) posso ignorarlo.
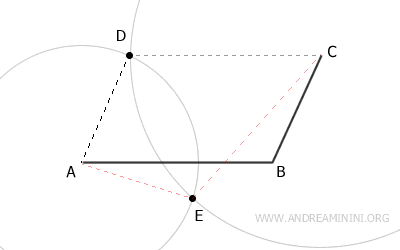
In questo caso il punto D è il quarto vertice del parallelogramma.
A questo punto, traccio il segmento CD
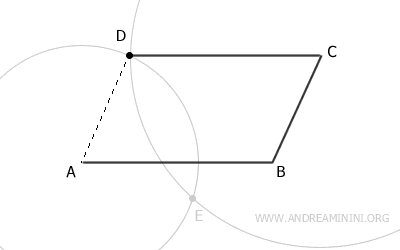
Infine, traccio il segmento AD, il quarto e ultimo lato del quadrilatero.
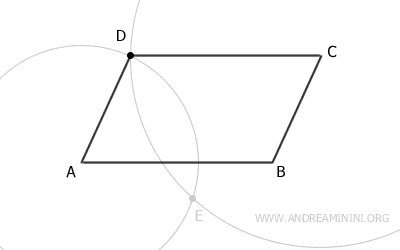
Il risultato è un parallelogramma ossia un quadrilatero con i lati opposti paralleli e congruenti.
Osservazioni
Alcune osservazioni, proprietà e note sul parallelogramma
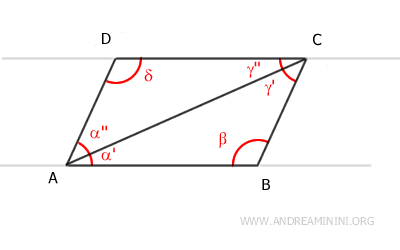
- Ogni lato e ogni diagonale del parallelogramma posso considerarlo come la trasversale che taglia due rette parallele
Questo mi permette di utilizzare le proprietà e il teorema delle rette parallele per determinare gli angoli del parallelogramma o nelle dimostrazioni.
- Ogni diagonale divide il parallelogramma in due triangoli congruenti
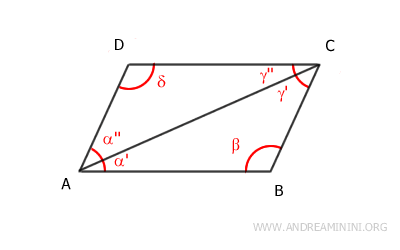
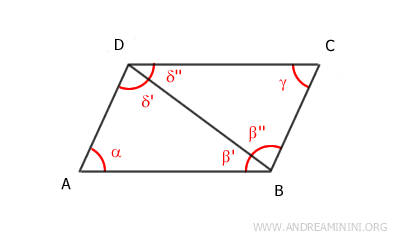
Dimostrazione. Considero la diagonale maggiore dal vertice A al vertice C. La diagonale divide il parallelogramma in due triangoli ACD e ABC. La diagonale AC è il lato in comune in entrambi i triangoli. Per il teorema delle rette parallele, gli angoli α' e γ'' sono congruenti α'≅γ'' perché sono angoli alterni interni dei segmenti AB e CD tagliati dalla trasversale AC. Anche gli angoli angoli α'' e γ' sono congruenti α''≅γ' per la stessa ragione, sono angoli alterni interni. Quindi, per il secondo criterio di congruenza (ALA) i due triangoli ACD e ABC sono triangoli congruenti ACD≅ABC.

Ora considero la diagonale minore dal vertice B al vertice D. La diagonale divide il parallelogramma in due triangoli ABD e BCD. La diagonale BD è il lato in comune in entrambi i triangoli. Per il teorema delle rette parallele, gli angoli β' e δ'' sono congruenti β'≅δ'' perché sono angoli alterni interni dei segmenti AB e CD tagliati dalla trasversale BD. Anche gli angoli angoli β'' e δ' sono congruenti β''≅δ' per la stessa ragione, sono angoli alterni interni. Quindi, per il secondo criterio di congruenza (ALA) i due triangoli ABD e BCD sono triangoli congruenti ABD≅BCD.
- I lati opposti del parallelogramma sono congruenti

Dimostrazione. Una diagonale divide il parallelogramma in due triangoli congruenti: ACD≅ABC. Essendo due triangoli congruenti, i lati dei due triangoli sono congruenti nello stesso ordine: CD≅AB , AD≅BC , mentre AC è il lato in comune. Questo dimostra la congruenza dei lati opposti del parallelogramma.

- Gli angoli opposti del parallelogramma sono congruenti
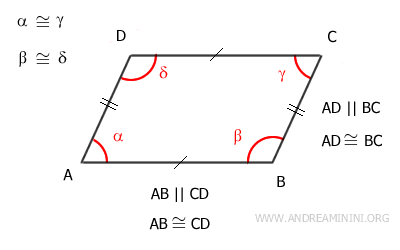
Dimostrazione. La diagonale maggiore AC divide il parallelogramma in due triangoli congruenti: ACD≅ABC. Quindi, gli angoli dei due triangoli sono congruenti nello stesso ordine: β≅δ, γ'≅α'', α'≅γ''. In particolar modo, mi interessa sapere che sono congruenti gli angoli β≅δ perché sono angoli opposti del parallelogramma.

Allo stesso modo la diagonale minore BD divide il parallelogramma in due triangoli congruenti: ADB≅BCD. Quindi, anche in questo caso gli angoli dei due triangoli sono congruenti nello stesso ordine: α≅γ, β'≅δ'', δ'≅β''. In particolar modo, mi interessa sapere che sono congruenti gli angoli α≅γ perché sono angoli opposti del parallelogramma.

- Gli angoli adiacenti a ogni lato del parallelogramma sono angoli supplementari (180°)
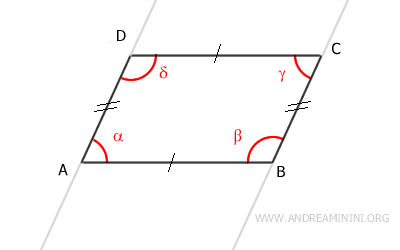
Dimostrazione. Gli angoli α e β sono gli angoli adiacenti al lato AB. Per il teorema delle rette parallele gli angoli α e β sono angoli supplementari (α+β=180°) perché sono gli angoli coniugati delle rette parallele AD||BC tagliate dalla trasversale AB. Lo stesso ragionamento posso ripeterlo per tutti gli altri angoli adiacenti del parallelogramma.
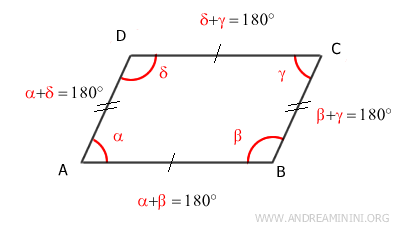
In questo modo posso dimostrare che tutti gli angoli adiacenti ai lati del parallelogramma sono angoli supplementari $$ \alpha + \beta = 180° $$ $$ \alpha + \delta = 180° $$ $$ \beta + \gamma = 180° $$ $$ \gamma + \delta = 180° $$ - Le diagonali si intersecano nel loro punto medio
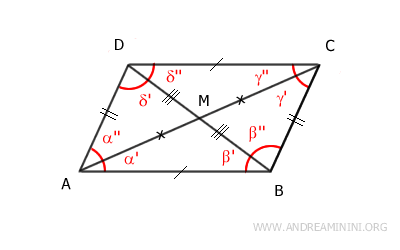
Dimostrazione. Traccio le due diagonali del parallelogramma AC e BD. I lati opposti del parallelogramma sono congruenti AB≅CD e AD≅BC. Per il teorema delle rette parallele gli angoli α'≅γ'' sono congruenti perché sono angoli alterni interni di due rette parallele AB||CD tagliate dalla retta AC. Sempre per il teorema delle rette parallele anche gli angoli β'≅δ'' sono congruenti perché sono angoli alterni interni di due rette parallele AB||CD tagliate dalla retta BD.
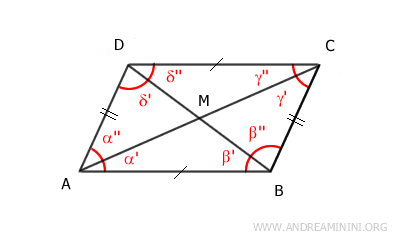
Quindi, per il secondo criterio di congruenza dei triangoli, i triangoli ABM e CDM sono congruenti, perché hanno un lato congruente AB≅CD e due angoli congruenti α'≅γ'' e β'≅δ''. Quindi i due triangoli hanno tutti i lati congruenti nello stesso ordine. In particolar modo mi interessa sapere che sono congruenti i segmenti AM≅MC e BM≅DM. Questo vuol dire il punto M è il punto medio delle diagonali AC e BD divide in due parti congruenti (di uguale lunghezza) sia la diagonale AC che la diagonale BD,

E così via.
