Formula di Erone

La formula di Erone permette di calcolare l'area di un triangolo conoscendo la lunghezza dei suoi tre lati. $$ A = \sqrt{p(p-a)(p-b)(p-c)} $$ Dove $a$, $b$, e $c$ sono i lati e $p$ è il semiperimetro del triangolo.

Il semiperimetro del triangolo è definito come

$$ p= \frac{a+b+c}{2} $$

Questa formula è particolarmente utile in quanto non richiede di conoscere l'altezza del triangolo, né l'ampiezza degli angoli.

Quindi rende più semplice il calcolo dell'area del triangolo quando l'altezza non è facilmente misurabile o calcolabile.

Nota. La formula prende il nome Erone di Alessandria, un matematico e ingegnere greco che visse nel 1° secolo d.C. Tuttavia, è probabile che fosse conosciuta anche prima della sua epoca.

La formula di Erone non richiede che il triangolo sia rettangolo o abbia alcuna proprietà particolare, può essere applicata su qualsiasi tipo di triangolo, a patto che si conoscano le lunghezze dei suoi lati.

Un esempio pratico

Considero un triangolo con lati di lunghezza a=8, b=15 e c=17.

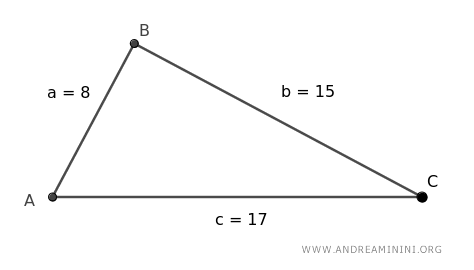
esempio di triangolo

Voglio calcolare l'area di questo triangolo.

In questo caso non conosco l'altezza, quindi non posso applicare immediatamente la classica formula dell'area di un triangolo, ovvero base per altezza diviso due.

$$ A = \frac{ \text{base} \ × \ \text{altezza} }{2} $$

Tuttavia, conosco tutte le lunghezze dei lati del triangolo.

Quindi, ricorro alla formula di Erone.

$$ A = \sqrt{p(p-a)(p-b)(p-c)} $$

Dove $a$, $b$, e $c$ sono le lunghezze dei lati del triangolo, mentre $ p $ è il semiperimetro.

Sostituisco le lunghezze dei lati del triangolo che già conosco: a=8, b=15 e c=17.

\[A = \sqrt{p(p - 8)(p - 15)(p - 17)}\]

Poi calcolo il semiperimetro $p$ del triangolo, che si ottiene sommando le lunghezze dei tre lati e dividendo il risultato per 2.

$$ p = \frac{a + b + c}{2} $$

$$ p = \frac{8 + 15 + 17}{2} = \frac{40}{2} = 20 $$

Nota. La ragione per cui si calcola il semiperimetro è perché serve come una specie di "punto medio" che mi aiuta a relazionare tutte e tre le lunghezze dei lati del triangolo con l'area. E' una sorta di valore che bilancia le lunghezze dei lati.

Sostituisco il semiperimetro $ p = 20 $ nella formula di Erone per trovare l'area $A$ del triangolo:

$$ A = \sqrt{20(20 - 8)(20 - 15)(20 - 17)} $$

$$ A = \sqrt{20 \times 12 \times 5 \times 3} $$

$$ A = \sqrt{3600} $$

$$ A = 60 $$

Quindi, l'area del triangolo con lati di 8, 15, e 17 unità è uguale a 60 unità quadrate.

Faccio una rapida verifica con Geogebra e il risultato è corretto.

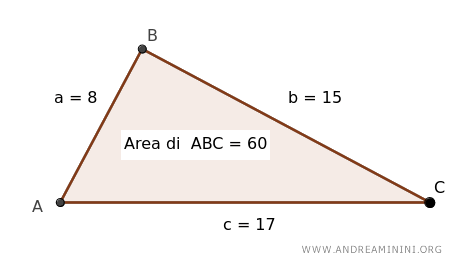
l'area del triangolo è A=20

Nota. La radice quadrata serve a "normalizzare" il prodotto di tutte queste differenze tra il semiperimetro $p$ e ciascun lato del triangolo.

E così via.