Il primo criterio di similitudine dei triangoli
Due triangoli sono simili se hanno due angoli congruenti nello stesso ordine.
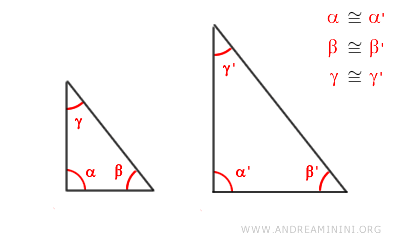
Se due triangoli hanno due coppie di angoli interni corrispondenti congruenti, deduco che anche il terzo angolo in ciascun triangolo deve essere congruente.
Questo perché la somma degli angoli interni in un triangolo è sempre uguale a 180 gradi
$$ \alpha + \beta + \gamma \cong 180° $$
Quindi, se due coppie di angoli corrispondenti sono congruenti, anche la terza coppia di angoli è congruente.
Di conseguenza, i due triangoli sono triangoli simili perché hanno tutti gli angoli congruenti nello stesso ordine, cioé mantengono la stessa forma pur potendo variare in dimensione.
$$ ABC \approx A'B'C' $$
Questo principio è anche noto come criterio di similitudine AAA (Angolo-Angolo-Angolo) dei triangoli.
Un esempio pratico
Considero due triangoli ABC e A'B'C'
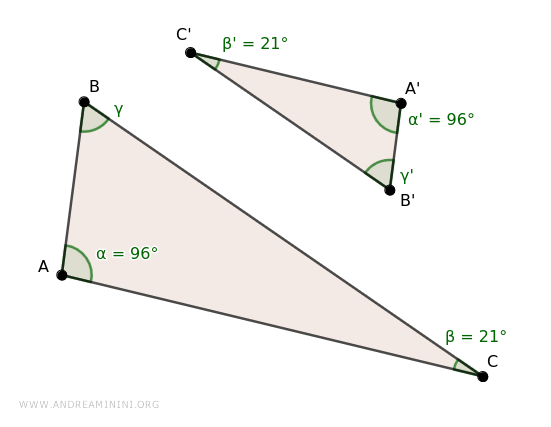
Questi triangoli hanno gli angoli ordinatamente α≅α' (96°) e β≅ β' (21°) congruenti.
Sapendo che la somma degli angoli interni in qualsiasi triangolo è uguale a 180°
$$ \alpha + \beta + \gamma = 180° $$
$$ \alpha ' + \beta ' + \gamma ' = 180° $$
Ricavo gli angoli γ e γ' dagli altri angoli di cui conosco l'ampiezza
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma ' = 180° - \alpha ' - \beta ' $$
Sostituisco α≅α'≅96°
$$ \gamma = 180° - 96° - \beta $$
$$ \gamma ' = 180° - 96° - \beta ' $$
Sostituisco β≅ β'≅21°
$$ \gamma = 180° - 96° - 21° $$
$$ \gamma ' = 180° - 96° - 21° $$
Quindi, deduco l'ampiezza degli angoli γ e γ' che ovviamente sono congruenti γ≅γ' perché sono ottenuti dalla somma algebrica di angoli congruenti
$$ \gamma = 63° $$
$$ \gamma ' = 63° $$
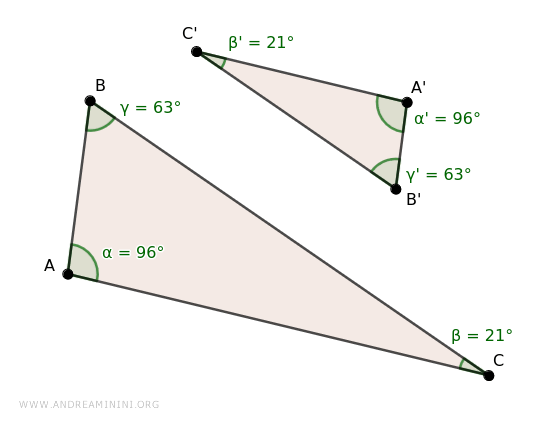
I triangoli ABC e A'B'C' hanno tutti gli angoli congruenti α≅α' (96°) , β≅ β' (21°) e γ≅γ' (63°).
Pertanto, sono triangoli simili.
La dimostrazione
Prendo in considerazione due triangoli ABC e A'B'C'
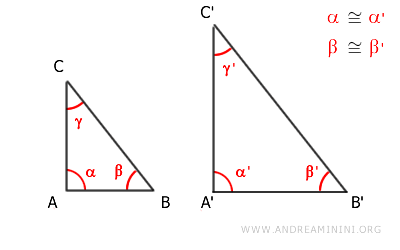
Per ipotesi iniziale gli angoli interni corrispondenti α≅α' e β≅β' sono congruenti.
$$ \alpha \cong \alpha ' $$
$$ \beta \cong \beta ' $$
Devo dimostrare che i due triangoli sono simili ossia ABC ≈A'B'C'
Per dimostrarlo basta analizzare la congruenza dei segmenti tra gli angoli corrispondenti ovvero tra i segmenti AB e A'B'

1) I segmenti AB e A'B' sono congruenti
Se i segmenti AB≅A'B' sono congruenti, allora i due triangoli ABC≅A'B'C' sono congruenti per il secondo criterio di congruenza dei triangoli.
Due figure geometriche congruenti sono anche simili con un rapporto di similitudine pari a 1.
Quindi, in questo caso la similitudine è dimostrata.
2) I segmenti AB e A'B' non sono congruenti
Se i due segmenti adiacenti agli angoli non sono congruenti, calcolo il rapporto k tra questi:
$$ k = \frac{\overline{A'B'}}{\overline{AB}} $$
Poi trasformo il triangolo ABC con una omotetia prendendo come centro C e il rapporto di similitudine pari a k=A'B'/AB
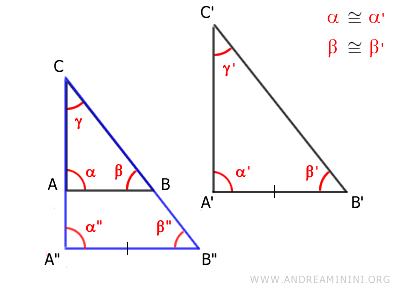
Per costruzione i segmenti A"B"≅A'B' sono congruenti perché A'B'=k·AB e anche A"B"=k·AB
$$ \overline{A''B''} \cong \overline{A'B'} $$
Inoltre, l'omotetia mantiene il parallelismo tra i segmenti, quindi deduco che A"B" e AB siano segmenti paralleli
$$ \overline{A''B''} \ || \ \overline{AB} $$
Di conseguenza, per il teorema delle rette parallele deduco che gli angoli α≅α" e β≅β" sono congruenti perché sono angoli corrispondenti ottenuti da trasversali che tagliano due rette parallele AB||A"B".
$$ \alpha \cong \alpha '' $$
$$ \beta \cong \beta '' $$
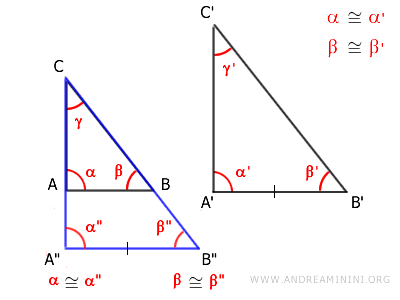
Sapendo per ipotesi iniziale che β≅β' e α≅α' deduco che anche α'≅α" e β'≅β" sono angoli congruenti.
$$ \alpha ' \cong \alpha '' $$
$$ \beta ' \cong \beta '' $$
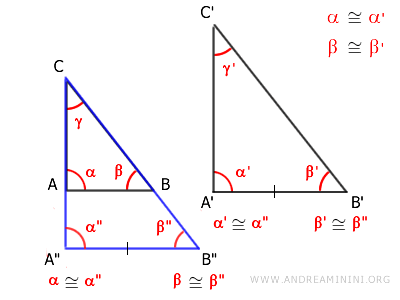
Pertanto, per il secondo criterio di congruenza dei triangoli, i triangoli A"B"C≅A'B'C' sono congruenti, perché hanno due angoli congruenti α'≅α" e β'≅β" e il lato adiacente congruente A"B"≅A'B.
Questo significa che il triangolo A'B'C' è congruente a un triangolo omotetico di ABC, pertanto i triangoli ABC e A'B'C' sono triangoli simili.
3) conclusione
In conclusione, in entrambi i casi (AB e A'B' adiacenti o meno) i due triangoli ABC e A'B'C' sono simili.
Questo dimostra il primo criterio di similitudine dei triangoli.
E così via.
