L'equazione della retta passante per due punti
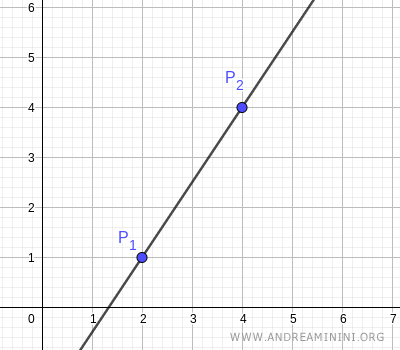
L'equazione di una retta passante per due punti distinti \( (x_1, y_1) \) e \( (x_2, y_2) \) del piano può essere trovata utilizzando la formula seguente: $$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} $$ In due punti distinti del piano passa una e una sola retta.
La retta passante per due punti distinti nello spazio \( (x_1, y_1, z_1) \) e \( (x_2, y_2, z_2) \) si ottiene con la formula $$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} = \frac{z-z_1}{z_2-z_1} $$ ossia $$ \begin{cases} \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} \\ \\ \frac{y-y_1}{y_2-y_1}= \frac{z-z_1}{z_2-z_1} \end{cases} $$ Purché i due punti siano distinti, ossia se $ x_1 \ne x_2 $ , $ y_1 \ne y_2 $ e $ z_1 \ne z_2 $
Questa formula è detta forma frazionaria della retta.
Permette di ottenere l'equazione della retta.
$$ ax+by+c=0 $$
E' anche detta "condizione di allineamento della retta" perché mi permette di verificare se tre punti \( (x,y) , (x_1, y_1) \) e \( (x_2, y_2) \) del piano sono allineati oppure no.
- Se il punto $ (x,y) $ soddisfa questa proporzione, allora sta sulla retta passante per $ (x_1,y_1) $ e $ (x_2,y_2) $.
- Se non la soddisfa, non è allineato con gli altri due.
Spesso viene presentata anche in questa forma equivalente.
$$ \frac{y-y_1}{x-x_1}= \frac{y_2-y_1}{x_2-x_1} $$
Dove $ m = \frac{y_2-y_1}{x_2-x_1} $ è il coefficiente angolare (m) della retta nella forma esplicita y=mx+q.
$$ \frac{y-y_1}{x-x_1}= m $$
Esempio
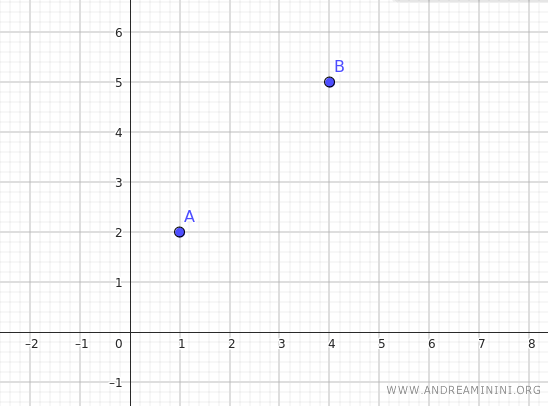
Devo trovare l'equazione della retta che passa per i punti diversi A e B del piano.
Il punto A si trova alle coordinate $ (x_1,y_1)=(1, 2) $ mentre il punto B alle coordinate $ (x_2,y_2)= (4, 5) $
Utilizzo la formula della retta passante per due punti.
$$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} $$
In questo caso le coordinate dei due punti sono x1=1, y1=2 e x2=4, y2=5.
$$ \frac{y-2}{5-2}= \frac{x-1}{4-1} $$
$$ \frac{y-2}{3}= \frac{x-1}{3} $$
Per la proprietà invariantiva delle equazioni moltiplico entrambi i membri per 3 e semplifico l'equazione.
$$ \frac{y-2}{3} \cdot 3= \frac{x-1}{3} \cdot 3 $$
$$ y-2 = x-1 $$
Sposto tutti i termini al primo membro dell'equazione.
$$ y - 2 - x + 1= 0 $$
$$ y - x -1 = 0 $$
Ho così trovato l'equazione in forma implicita y-x-1=0 della retta passante per i due punti (1,2) e (4,5).
Per passare alla forma esplicita basta ricavare la variabile y in funzione di tutto il resto.
$$ y = x+1 $$
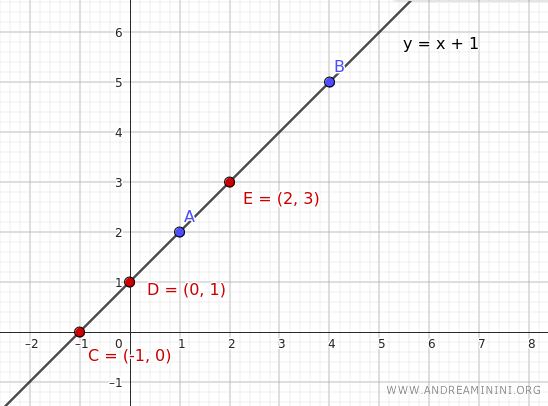
A questo punto sostituisco alla variabile indipendente x altri valori per ottenere i corrispondenti valori della variabile dipendente y.
$$ \begin{array}{c|c} x & y=x+1 \\ \hline -1 & 0 \\ 0 & 1 \\ 1 & 2\\ 2 & 3 \end{array} $$
In questo modo ottengo tutti gli altri punti appartenenti alla retta.
Soluzione alternativa
In alternativa, posso usare le coordinate dei due punti per calcolare il coefficiente angolare (m) ovvero la pendenza della retta che passa attraverso questi due punti è dato da:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Questa formula mi dice quanto la retta "sale" o "scende" man mano che ci si sposta da sinistra a destra lungo l'asse delle x.
Sapendo che le coordinate dei due punti sono x1=1, y1=2 e x2=4, y2=5.
$$ m = \frac{5 - 2}{4 - 1} $$
$$ m = \frac{3}{3} $$
$$ m = 1 $$
Una volta che hai il coefficiente angolare, puoi usare la forma punto-pendenza dell'equazione di una retta, che è:
$$ y - y_1 = m \cdot (x - x_1) $$
Sostituisco m=1.
$$ y - y_1 = 1 \cdot (x - x_1) $$
$$ y - y_1 = x - x_1 $$
Sapendo che x1=1, y1=2
$$ y - 2 = x - 1 $$
Ricavo la y e ottengo l'equazione della retta
$$ y = x - 1 + 2 $$
$$ y = x + 1 $$
Il risultato finale è sempre lo stesso.
L'equazione della retta che passa per i punti \( (1, 2) \) e \( (3, 8) \) è \( y = 3x - 1 \).
Esempio 2
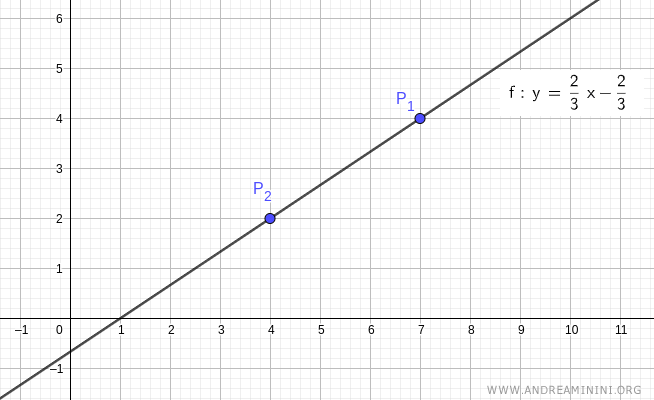
Considero due punti distinti del piano P1(7;4) e P2(4;2).
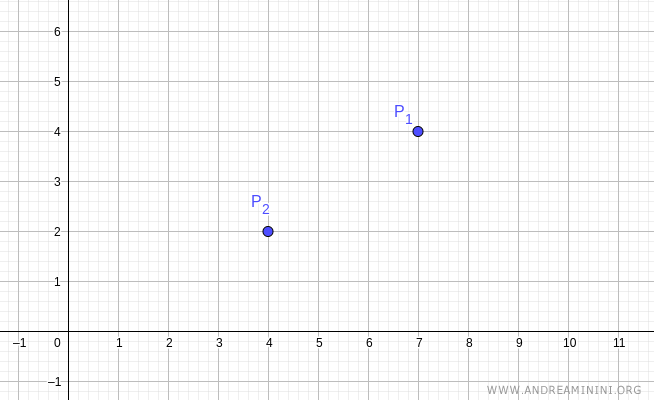
L'equazione della retta passante per i due punti P1 e P2 è la seguente
$$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} $$
In questo caso (x1;y1)=(7;4) e (x2;y2)=(4;2)
Sostituisco x1=7, x2=4, y1=4, y2=2
$$ \frac{x-7}{4-7} = \frac{y-4}{2-4} $$
$$ \frac{x-7}{-3} = \frac{y-4}{-2} $$
Esplicito la y
$$ \frac{x}{-3} + \frac{-7}{-3} = \frac{y}{-2} + \frac{-4}{-2} $$
$$ \frac{y}{-2} = \frac{x}{-3} + \frac{-7}{-3} - 2 $$
$$ y = (-2) \cdot [ \frac{x}{-3} + \frac{7-6}{3} ] $$
$$ y = (-2) \cdot [ \frac{x}{-3} + \frac{1}{3} ] $$
$$ y = \frac{2}{3}x - \frac{2}{3} $$
Questa è l'equazione esplicita della retta passante per i due punti P1(7;4) e P2(4;2).
Al variare di x ottengo tutti i punti della retta.
Esempio 3
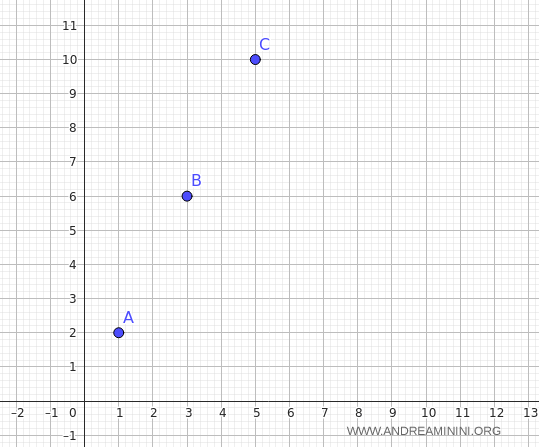
Considero tre punti del piano
$$ A(1,2), \quad B(3,6), \quad C(5,10). $$
I punti $A, B, C$ sono allineati oppure no?
Per verificarlo posso usare la formula frazionaria.
Prendo i primi due punti $A$ e $B$:
$$ x_1 = 1, \; y_1 = 2, \quad x_2 = 3, \; y_2 = 6. $$
La condizione di allineamento per $C(x,y) = (5,10)$ è:
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
$$ \frac{10 - 2}{6 - 2} = \frac{5 - 1}{3 - 1} $$
$$ \frac{8}{4} = \frac{4}{2} \quad \Rightarrow \quad 2 = 2 $$
L'equazione è vera, quindi i tre punti sono allineati, ossia per i tre punti passa una retta.
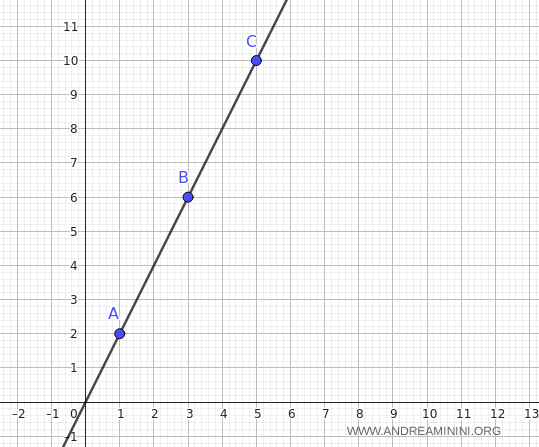
E qual è l'equazione di questa retta? Considero due punti, ad esempio $$ A(1,2), \quad B(3,6) $$ Trovo il coefficiente angolare $m$ $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2 $$ Scrivo l’equazione in forma esplicita usando la forma punto-pendenza con il punto $A(1,2)$: $$ y - y_1 = m(x - x_1) $$ cioè: $$ y - 2 = 2(x - 1) $$ Svolgo i calcoli: $$ y = 2(x - 1) + 2 $$ $$ y = 2x - 2 + 2 $$ $$y = 2x $$ Quindi l’equazione in forma esplicita della retta che passa per i tre punti è $ y=2x $ Per ottenere anche la l'equazione della retta in forma implicita $ax + by + c = 0$ parto dalla forma esplicita $ y= 2x $ e porto tutti i termini a sinistra: $$ y - 2x = 0 $$ Moltiplico eventualmente per $-1$, non obbligatorio... ma spesso si scrive con $x$ positivo $$ 2x - y = 0 $$ Quindi la forma implicita della retta è: $$ 2x - y = 0 $$
Soluzione alternativa
Per rispondere alla domanda utilizzo il metodo dei coefficienti angolari.
Calcolo il coefficiente angolare $m_{AB}$:
$$ m_{AB} = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2 $$
Calcolo il coefficiente angolare $m_{BC}$:
$$ m_{BC} = \frac{10 - 6}{5 - 3} = \frac{4}{2} = 2 $$
Poiché $m_{AB} = m_{BC}$, i tre punti sono allineati.
Metodo 3 (Area del triangolo). Un altro modo è calcolare l’area del triangolo $ABC$: $$ \text{Area} =
\frac{1}{2}\left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| $$ Sostituisco i dati $$ \begin{align} \text{Area} &= \frac{1}{2}\left| 1(6 - 10) + 3(10 - 2) + 5(2 - 6) \right| \\ &= \frac{1}{2} | -4 + 24 - 20 | \\ &= \frac{1}{2}\cdot 0 = 0 \end{align} $$ L’area è zero, quindi i punti sono allineati.
Esempio 4
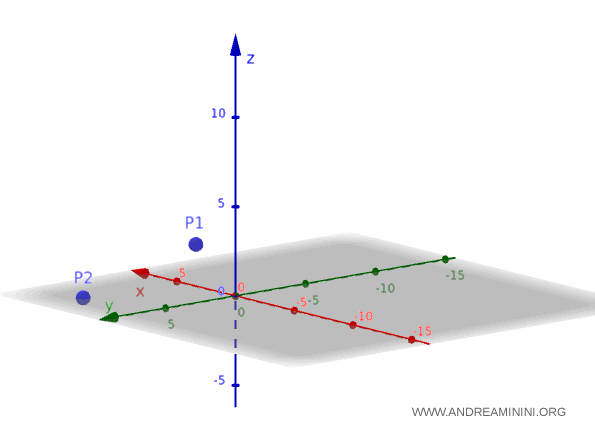
Considero due punti nello spazio $ \mathbb{R}^3 $
$$ P_1(1,2,3), \quad P_2(5,6,7) $$
Devo trovare l’equazione della retta passante per $P_1$ e $P_2$
Scrivo il sistema di equazioni:
$$ \begin{cases}
\dfrac{y - y_1}{y_2 - y_1} = \dfrac{x - x_1}{x_2 - x_1} \\ \\
\dfrac{y - y_1}{y_2 - y_1} = \dfrac{z - z_1}{z_2 - z_1}
\end{cases} $$
Sostituisco le coordinate dei punti $ P_1(1,2,3) $ e $ P_2(5,6,7) $
$$ \begin{cases}
\dfrac{y - 2}{6 -2} = \dfrac{x - 1}{5 -1} \\ \\
\dfrac{y - 2}{6 - 2} = \dfrac{z - 3}{7-3}
\end{cases} $$
$$ \begin{cases}
\dfrac{y - 2}{4} = \dfrac{x - 1}{4} \\ \\
\dfrac{y - 2}{4} = \dfrac{z - 3}{4}
\end{cases} $$
Semplifico moltiplicando entrambi i membri di ogni equazione per 4.
$$ \begin{cases}
y - 2= x - 1 \\ \\
y - 2= z - 3
\end{cases} $$
Infine risolvo la prima equazione per $ x $ e la seconda per $ y $
$$ \begin{cases}
x = y - 2 + 1 \\ \\
y = z - 3 + 2
\end{cases} $$
La retta è rappresentata dal sistema di equazioni ridotte:
$$ \begin{cases}
x = y - 1 \\ \\
y = z - 1
\end{cases} $$
Ecco la rappresentazione grafica della retta passante per i due punti $ P_1 $ e $ P_2 $ nello spazio tridimensionale.
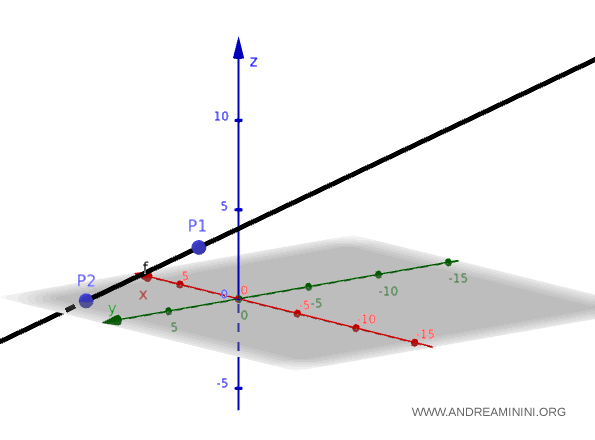
Nota. Per verificare se un punto, ad esempio $ Q(9,10,11), $ appartiene alla retta, sostituisco le coordinate del punto nel sistema e verifico se le equazioni sono soddistatte. $$ \begin{cases} x = y - 1 \\ \\ y = z - 1 \end{cases} $$ $$ \begin{cases} 9 = 10 - 1 \\ \\ 10 = 11 - 1 \end{cases} $$ $$ \begin{cases} 9 = 9 \\ \\ 10 = 10 \end{cases} $$ Entrambe le equazioni sono vere, quindi il punto Q appartiene alla retta.
La dimostrazione
Per dimostrare la formula della retta passante per due punti considero tre punti del piano (x1;y1), (x2;y2), (x;y)
Ipotizzo che in ciascun punto passi la stessa retta.
Quindi costruisco un sistema di equazioni.
$$ \begin{cases} ax_1+by_1+c=0 \\ ax_2+by_2+c=0 \\ ax+by+c=0 \end{cases} $$
Utilizzo il metodo della riduzione e sottraggo la prima equazione dalla seconda e dalla terza equazione.
$$ \begin{cases} a(x_2-x_1)+b(y_2-y_1)=0 \\ a(x-x_1)+b(y-y_1)=0 \end{cases} $$
$$ \begin{cases} a(x_2-x_1) = - b(y_2-y_1) \\ a(x-x_1) = - b(y-y_1) \end{cases} $$
$$ \begin{cases} \frac{x_2-x_1}{y_2-y_1}= - \frac{b}{a} \\ \frac{x-x_1}{y-y_1}= - \frac{b}{a} \end{cases} $$
Dal confronto delle due equazioni è evidente che entrambe uguali a -b/a.
Quindi posso scrivere l'uguaglianza in questo modo:
$$ \frac{x_2-x_1}{y_2-y_1}= \frac{x-x_1}{y-y_1} $$
Infine, con un semplice passaggio algebrico ottengo la condizione di allineamento dei punti di una retta
$$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} $$
Questo dimostra la formula dell'equazione della retta passante per due punti distinti (x1;y1) e (x2,y2) del piano.
Dimostrazione alternativa
Considero due punti distinti del piano P1(x1;y2) e P2(x2;y2)
Applico il concetto di fascio di rette per ricavare l'equazione delle rette che passano per il punto P1
$$ y - y_1 = m (x-x_1) $$
Dove m è il coefficiente angolare delle rette e può assumere infiniti valori, uno per ogni inclinazione delle rette ad eccezione della retta parallela all'asse y.
La retta che passa per i punti P1 e P2 ha il seguente coefficiente angolare.
$$ m = \frac{y_2-y_1}{x_2-x_1} $$
Sostituisco il coefficiente angolare nell'equazione del fascio di rette passanti per il punto P1
$$ y - y_1 = m (x-x_1) $$
$$ y - y_1 = \frac{y_2-y_1}{x_2-x_1} (x-x_1) $$
Separo le variabili y e x nei due membri dell'equazione
$$ \frac{y - y_1}{y_2-y_1} = \frac{x-x_1}{x_2-x_1} $$
Il risultato è l'equazione della retta passante per i due punti.
La retta passante per due punti in algebra lineare
La retta passante tra due punti posso dimostrarla anche usando il linguaggio dell'algebra lineare.
Questa seconda dimostrazione richiede la conoscenza del calcolo vettoriale e matriciale.
La dimostrazione
Dati due punti del piano
$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} $$ $$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$
La retta passante per i due punti P2 e P1 equivale al seguente vettore direttore P2P1:
$$ v_r \equiv \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$
Dato il vettore direttore posso scrivere l'equazione vettoriale della retta che è uguale a
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$
Dalla quale ricavo il sistema di equazioni parametriche della retta partendo da P1
$$ \begin{cases} x = x_1 + t_1 \cdot ( x_2 - x_1 ) \\ y = y_1 + t_1 \cdot ( y_2 - y_1 ) \end{cases} $$
Nota. Partendo da P2 otterrei delle equazioni parametriche diverse ma il risultato finale sarebbe comunque lo stesso. Quindi, per continuare questa dimostrazione posso indifferentemente scegliere uno dei due sistemi di equazioni parametriche. $$ \begin{cases} x = x_2 + t_2 \cdot ( x_2 - x_1 ) \\ y = y_2 + t_2 \cdot ( y_2 - y_1 ) \end{cases} $$
Dato un punto generico P della retta, questo forma un vettore rispetto al punto P1.
$$ \overrightarrow{P_1P} = P - P_1 = \begin{pmatrix} x - x_1 \\ y - y_1 \end{pmatrix} $$
Il vettore P1P deve essere un vettore parallelo e proporzionale al vettore direttore P1P2 poiché si trova sulla retta r equivalente al vettore direttore vr.
Pertanto, i due vettori P1P e P1P2 devono essere vettori linearmente dipendenti.
Ponendo i due vettori in colonna in una matrice, il determinante è nullo.
$$ det \begin{pmatrix} x-x_1 & x_2-x_1 \\ y-y_1 & y_2 - y_1 \end{pmatrix} = 0 $$
Svolgo i calcoli del determinante e ottengo
$$ ( x-x_1) \cdot (y_2-y_1) - (x_2 - x_1) \cdot (y - y_1) = 0 $$
Dalle quali ricavo l'equazione cartesiana della retta con pochi passaggi algebrici.
$$ ( x-x_1) \cdot (y_2-y_1) = (x_2 - x_1) \cdot (y - y_1) $$
$$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} $$
Ho così determinato la formula dell'equazione generale della retta passante tra due punti.
La dimostrazione finisce qui.
Un esempio pratico
Dati due punti del piano P1 e P2
$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = P_1 \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$
$$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = P_2 \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$
La cui rappresentazione grafica è la seguente:
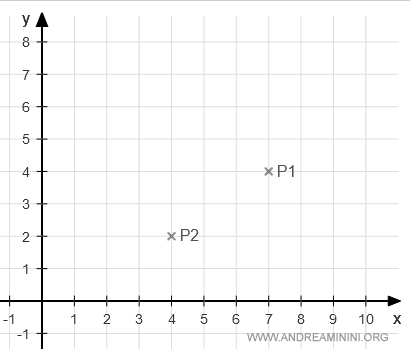
Fisso un verso da P1 a P2 e ottengo un vettore P1P2
$$ \overrightarrow{P_1P_2} = P_2 - P_1 = \begin{pmatrix} 4 \\ 2 \end{pmatrix} - \begin{pmatrix} 7 \\ 4 \end{pmatrix} = \begin{pmatrix} 4-7 \\ 2-4 \end{pmatrix} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$
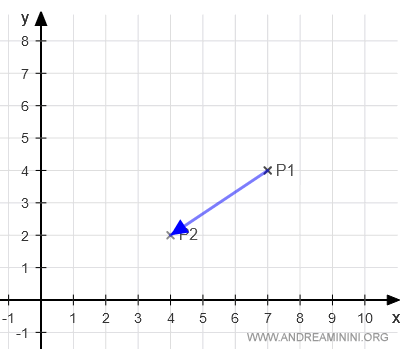
L'equazione vettoriale della retta è uguale a
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 4 - 7 \\ 2 -4 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$
Da questa ottengo l'equazione parametrica della retta
$$ \begin{cases} x = 7 - 3t \\ y = 4 - 2t \end{cases} $$
Tramite l'equazione parametrica posso tracciare tutti i punti della retta variando il valore del parametro t.
Pertanto, un generico punto mobile della retta è il seguente:
$$ P \begin{pmatrix} 7 - 3t \\ 4 - 2t \end{pmatrix} \:\: con \:\: t \:\: \in \:\: R $$
Con il parametro t=0 si ottiene il punto P1 ossia il punto iniziale del vettore P1P2.
Incrementando il parametro t, il punto si muove verso il punto P2.
Quando il parametro è t=1, si ottiene il punto P2 ossia il punto finale del vettore P1P2.
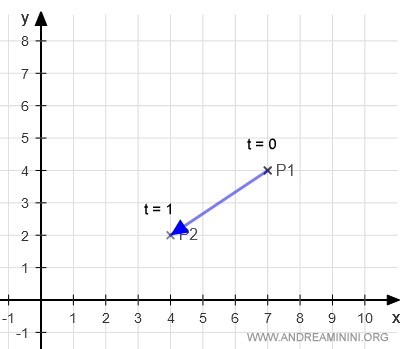
A questo punto devo trovare le equazioni cartesiane.
Per i punti P1 e P2 passa anche una retta r.
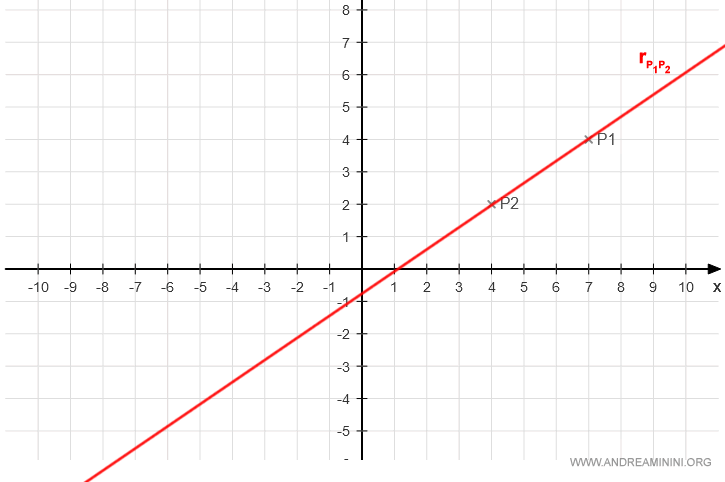
Dato un generico punto P della retta r
$$ P \begin{pmatrix} x \\ y \end{pmatrix} $$
Il punto P e il punto iniziale P1 formano un altro vettore P1P
$$ \overrightarrow{P_1P} = \begin{pmatrix} x \\ y \end{pmatrix} - \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$
$$ \overrightarrow{P_1P} = \begin{pmatrix} x-7 \\ y-4 \end{pmatrix} $$
Il vettore P1P che giace sulla retta r è proporzionale al vettore geometrico P2P1 di prima ( ossia vr ), perché la retta r passa per gli stessi punti P1 e P2.
$$ \overrightarrow{P_1P} = \begin{pmatrix} x-7 \\ y-4 \end{pmatrix} $$
$$ \overrightarrow{P_1P_2} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$
I due vettori sono vettori proporzionali se sono linearmente dipendenti.
In questo caso il determinante della matrice formata con i vettori in colonna deve essere uguale a zero.
$$ det \begin{pmatrix} x-7 & -3 \\ y-4 & -2 \end{pmatrix} = 0 $$
Svolgo i calcoli del determinante e ottengo l'equazione cartesiana della retta.
$$ (x-7) (-2) - (-3) (y-4) = 0 $$
$$ -2x + 14 + 3y - 12 = 0 $$
$$ -2x + 3y + 2 = 0 $$
Posso così calcolare una delle due coordinate x, y della retta in funzione dell'altra.
$$ y = \frac{2x - 2}{3} $$
A cosa serve conoscere l'equazione cartesiana? Mi permette di capire se un punto del piano con coordinate (x,y) appartiene o meno alla retta.
E così via.
