Fascio proprio di rette

Un fascio proprio di rette è l'insieme di tutte le rette che convergono in un punto specifico (A) del piano, noto come il centro del fascio.

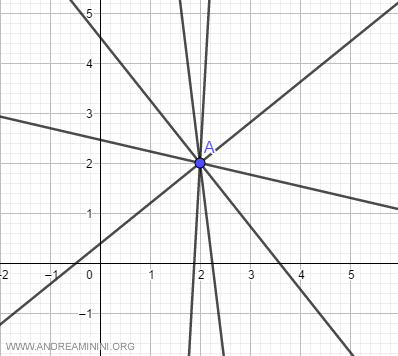
L'equazione del fascio proprio di rette centrato in un punto di coordinate \((x_0, y_0)\) è data da:

$$ y-y_0 = m \cdot (x-x_0) $$

Questa equazione descrive tutte le rette del fascio che passano per il punto \( (x_0, y_0) \), al variare del coefficiente angolare \( m \in \mathbb{R} \), eccetto la retta parallela all'asse delle ordinate \(y\).

Nota. La retta parallela all'asse delle ordinate non può essere espressa tramite l'equazione in forma esplicita \( y = mx \) poiché non esiste un valore di \( m \) che possa rappresentarla. Per le rette parallele all'asse delle ascisse \(x\), si utilizza invece l'equazione: $$ x = x_0 $$

In generale, dato un punto P di coordinate $ (x 0,; y 0 ) $ il fascio di rette di centro P ha le seguenti equazioni:

$$
\begin{cases}
y - y_0 = m \cdot (x - x_0) & \text{se la retta non è parallela all'asse y} \\
x = x_0 & \text{se la retta è parallela all'asse y}
\end{cases}
$$

L'insieme di tutte le rette che convergono nel centro di fascio è detto fascio completo.

In alternativa,  posso rappresentare le rette del fascio proprio di rette con centro C anche in questa forma: $$ y-y_0 = -\frac{h}{k} \cdot (x-x_0) $$ Dove h e k sono due numeri interi qualsiasi $ h,k \in \mathbb{Z} $ con k≠0.

Un esempio pratico

Prendo come esempio un punto del piano P(2,3) che considero come centro di fascio

Poi utilizzo le equazioni del fascio proprio di rette.

$$
\begin{cases}
y - y_0 = m \cdot (x - x_0) \\
x = x_0
\end{cases}
$$

In questo caso le coordinate del centro di fascio P(2,3) sono x₀=2 e y₀=3

$$
\begin{cases}
y - 3 = m \cdot (x - 2) \\
x = 2
\end{cases}
$$

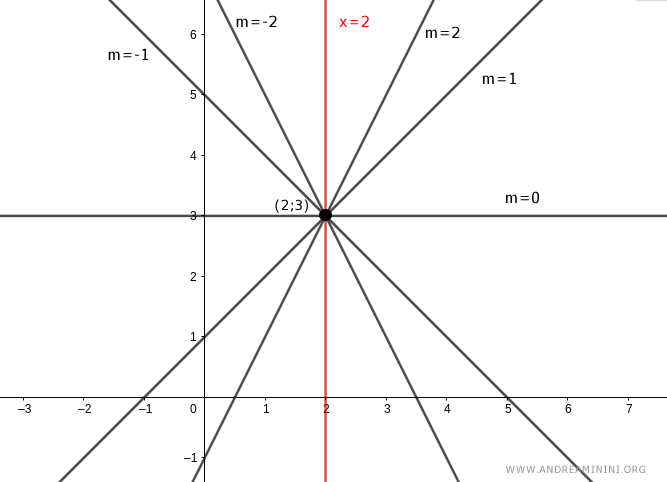
L'equazione \( y - 3 = m(x - 2) \) rappresenta un fascio di rette che passano per il punto \( (2, 3) \). Questo fascio include tutte le possibili rette con vari coefficienti angolari \( m \), ad eccezione di quelle parallele all'asse \( y \).

L'equazione \( x = 2 \), che descrive una retta di colore rosso, rappresenta la retta parallela all'asse \( y \) che passa per il punto \( (2, 3) \).

Ecco alcune rette del fascio completo di rette con centro P(2,3).

Esempio 2

In questo esempio prendo come riferimento un punto C

$$ C = \begin{pmatrix} x_0 = 2 \\ y_0 = 3 \end{pmatrix} $$

Rappresento le rette del fascio di rette con centro C usando questa equazione:

$$ y-y_0 = -\frac{h}{k} \cdot (x-x_0) $$

Dove h e k sono due numeri interi qualsiasi $ h,k \in \mathbb{Z} $ con k≠0 per evitare il problema della divisione per zero.

$$ y-3 = -\frac{h}{k} \cdot (x-2) $$

Poi ricavo y e ottengo l'equazione della retta in forma esplicita.

$$ y = -\frac{h}{k} \cdot (x-2) + 3 $$

Per ogni combinazione dei parametri h e k esiste una retta passante per il punto C.

Quindi, per ottenere il fascio completo di rette mi basta far variare il rapporto h/k.

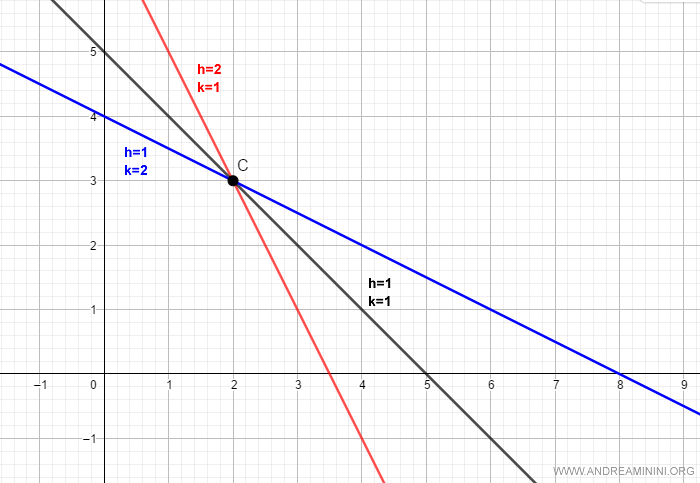
Anche in questo caso la retta parallela all'asse delle ordinata va rappresentata con un'equazione a parte ovvero con $ x=x_0 $ che in questo caso è $ x = 2 $.

La dimostrazione

Un fascio di rette proprio ha come centro il punto P alle coordinate (x₀;y₀)

$$ P(x_0;y_0) $$

Una generica retta del fascio proprio deve passare per il punto P(x₀;y₀)

$$ y = mx +q $$

Sostituisco y=y₀ e x=x₀

$$ y_0 = mx_0 +q $$

Poi esplicito il termine q

$$ q = y_0 -mx_0 $$

Sostituisco il termine q=y₀-mx nell'equazione generica di una retta.

$$ y = mx +q $$

$$ y = mx + (y_0 -mx_0) $$

$$ y = mx + y_0 -mx_0 $$

Separo le variabili y e x nei due membri dell'equazione

$$ y - y_ 0 = mx -mx_0 $$

$$ y - y_ 0 = m (x -x_0) $$

Il risultato finale è l'equazione del fascio proprio di rette.

Nota. L'equazione rappresenta tutte le rette del fascio proprio tranne la retta parallela all'asse x. Per quest'ultima devo usare un'equazione apposita x=x₀.

Dimostrazione alternativa

Se il punto A del piano ha le seguenti coordinate

$$ A = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$

allora l'equazione cartesiana di tutte le rette del fascio proprio di rette è

$$ h(x-x_0) + k(y-y_0) = 0 $$

Dove h e k sono coefficienti che ancora non conosco

Divido entrambi i membri dell'equazione per k.

$$ \frac{h(x-x_0)}{k} + \frac{k(y-y_0)}{k} = 0 $$

$$ \frac{h(x-x_0)}{k} + y-y_0 = 0 $$

Poi separo le variabili y e x nei due membri dell'equazione

$$ y-y_0 = -\frac{h}{k} \cdot (x-x_0) $$

Il rapporto -h/k è il coefficiente angolare (m) delle rette.

Lo sostituisco con m e riscrivo l'equazione del fascio delle rette in forma esplicita.

$$ y-y_0 = m \cdot (x-x_0) $$

Ogni retta del fascio proprio di rette è individuata da un particolare valore del coefficiente angolare m.

Attenzione. Nel caso particolare in cui la retta è parallela all'asse y, ossia è verticale, l'equazione non funziona perché m è indeterminata. In questo caso l'equazione della retta è x-x₀=0.

Le rette generatrici del fascio di rette

Per generare un fascio di rette proprio posso scegliere due rette incidenti r e s dette generatrici del fascio.

$$ ax+by+c=0 $$

$$ a'x+b'y+c'=0 $$

Il fascio di rette proprio è generato considerando ogni possibile combinazione lineare di queste due rette:

$$ p \cdot (ax+by+c) + q ( a'x+b'y+c') = 0 $$

Dove p e q sono scalari.

Per ottenere una forma equivalente più sintetica, divido entrambi i lati dell'equazione per p.

$$ \require{cancel} \frac{  \cancel{p}\cdot (ax+by+c)}{ \cancel{p}} + \frac{q ( a'x+b'y+c')}{p} = \frac{0}{p} $$

$$ ax+by+c + \frac{q}{p} \cdot ( a'x+b'y+c') = 0 $$

Diciamo che p sia sempre non nullo p≠0 per evitare il problema di una divisione per zero.

Introduco il parametro $ k = \frac{q}{p} $ per semplificare una forma ulteriormente semplificata:

$$ ax+by+c + k \cdot ( a'x+b'y+c') = 0 $$

Dove k è un numero razionale qualsiasi e ogni valore di k corrisponde una retta del fascio di rette.

Questa equazione rappresenta tutte le rette del fascio eccetto la retta a′x+b′y+c′=0, che non può essere ottenuta da questa forma perché richiederebbe che k tenda all'infinito.

Nota. La retta ax+by+c=0 posso generarla ponendo k=0 oppure q/p=0. Viceversa, la retta a'x+b'y+c'=0 non c'è modo di generarla nella forma $$ (ax+by+c) + k \cdot ( a'x+b'y+c') = 0 $$ Posso al massimo approssimarla facendo tendere a infinito il parametro $ k \rightarrow \infty $ . L'unico modo per ottenere la retta dell'equazione $ a'x+b'y+c' = 0 $ sarebbe tornare alla combinazione lineare iniziale assegnando i valori p=0 e q=1 ai coefficienti $$ p \cdot (ax+by+c) + q ( a'x+b'y+c') = 0 $$

Quale rette generatrici scegliere per costruire un fascio di rette con centro in P(x₀;y₀)?

Tutte le rette incidenti che passano per il punto P(x0;y0) vanno bene.

Tuttavia, per semplificare i calcoli è meglio scegliere quelle parallele agli assi cartesiani che passano per P(x0;y0).

$$ y = y_0 $$

$$ x = x_0 $$

ovvero le equazioni delle rette

$$ y - y_0 = 0 $$

$$ x - x_0 = 0 $$

In questo modo l'equazione del fascio di rette diventa

$$ p \cdot ( y-y_0 ) + q ( x-x_0 ) = 0 $$

$$ (y -y_0) + \frac{q}{p} \cdot ( x-x_0) = 0 $$

Nota. Il risultato finale è equivalente alla formula dell'equazione di una retta che passa in un punto con un coefficiente angolare $ m= - \frac{q}{p} $.  $$ y = m \cdot ( x-x_0) + y_0 $$

Quale retta del fascio passa per l'origine degli assi?

Per trovare il valore di \( k \) che genera una retta passante per l'origine O(0;0) degli assi cartesiani, considero l'equazione del fascio proprio

$$ (ax+by+c) + k \cdot (a'x+b'y+c') = 0 $$

La retta che voglio trovare deve passare per i punti x=0 e y=0.

Quindi, sostituisco questi valori nell'equazione del fascio di rette e ottengo:

$$ a \cdot 0 + b \cdot 0 + c + k \cdot (a' \cdot 0 + b' \cdot 0 + c') = 0 $$

$$ c + k \cdot c' = 0 $$

Infine, ricavo k

$$ k \cdot c' = -c $$

$$ k = -\frac{c}{c'} $$

Questo è il valore di \( k \) che genera una retta del fascio che passa per l'origine, a condizione che \( c' \neq 0 \) per evitare la divisione per zero.

Nota. Se \( c' = 0 \) e \( c \neq 0 \), non esiste un valore finito di \( k \) per cui la retta passa per l'origine. Se entrambi \( c \) e \( c' \) sono zero, ogni valore di \( k \) soddisfa l'equazione e questo indica che tutte le rette del fascio passano per l'origine.

Esempio

Considero due rette generatrici nel piano cartesiano, definite dalle seguenti equazioni:

$$  r: \ 2x + 3y + 4 = 0 $$

$$ s: \  x - 2y + 1 = 0 $$

Essendo due rette incidenti, posso sceglierle come generatrici del fascio di rette proprio.

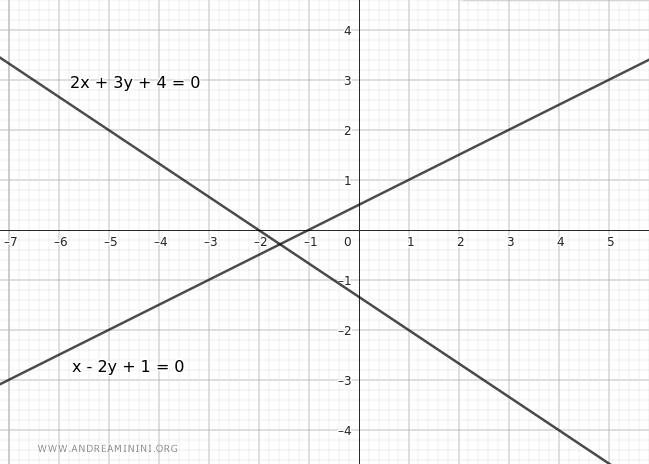
Utilizzo la loro combinazione lineare per esprimere il fascio:

$$ (2x + 3y + 4) + k \cdot (x - 2y + 1) = 0 $$

Espando e raccolgo i termini simili:

$$ (2 + k)x + (3 - 2k)y + (4 + k) = 0 $$

Questa equazione genera le rette del fascio di rette al variare del parametro k, ad eccezione della retta $ s: \  x - 2y + 1 = 0 $.

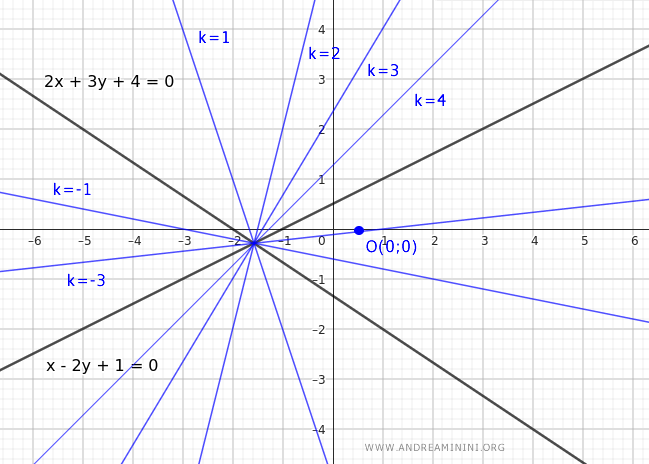
Nota. La retta $ s: x-2y+1=0 $ devo aggiungerla a parte nel fascio di rette perché non corrisponde a nessun valore k.

Qual è l'equazione della retta che passa per l'origine?

Per trovare la retta del fascio che passa per l'origine, impongo che l'equazione sia soddisfatta per \( x = 0 \) e \( y = 0 \):

$$ (2 + k) x + (3 - 2k)y + (4 + k) = 0 $$

$$ (2 + k) \cdot 0 + (3 - 2k) \cdot 0 + (4 + k) = 0 $$

$$ 4 + k = 0 $$

Risolvo per k e ottengo k=-4

$$ k = -4 $$

Sostituisco k=-4 nell'equazione del fascio di rette e in questo modo ottengo l'equazione della retta che passa per l'origine degli assi:

$$ (2 - 4)x + (3 + 8)y + (4 - 4) = 0 $$

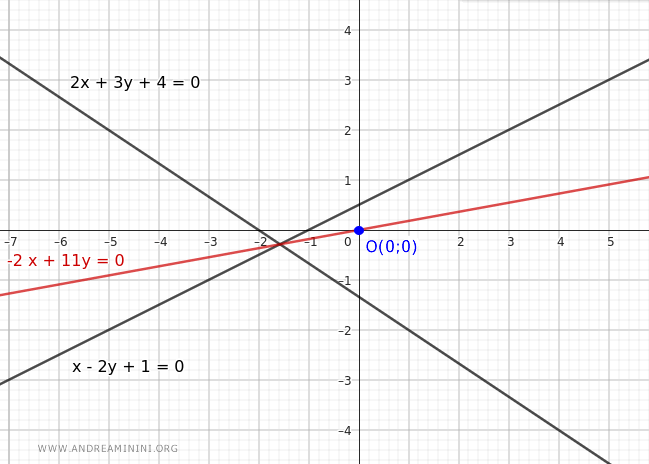
$$ -2x + 11y = 0 $$

$$ y =  \frac{2}{11}x $$

Questa è l'equazione della retta del nostro fascio che passa per l'origine.

Esempio 2

In questo esempio voglio costruire un fascio di rette con centro in un punto specifico, come P(2;3).

$$ P (2;3) $$

Per prima cosa scelgo due rette incidenti che passano nel punto P da utilizzare come generatrici del fascio.

Potrei scegliere tra infinite rette ...ma è molto più semplice utilizzare le rette parallele agli assi come generatrici:

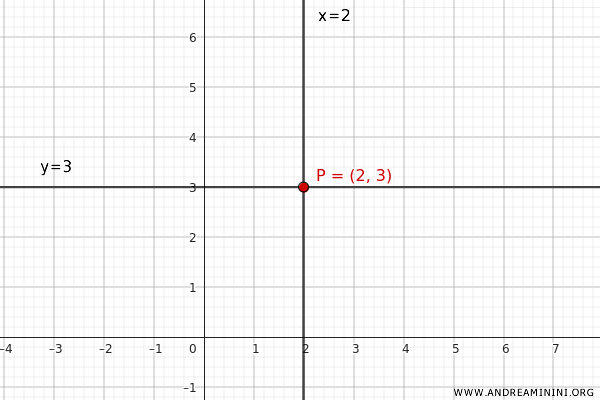
1. Una retta parallela all'asse \(x\) e passante per \( (2,3) \), che ha equazione \( y = 3 \) ovvero $ y - 3 = 0 $.
2. Una retta parallela all'asse \(y\) e passante per \( (2,3) \), che ha equazione \( x = 2 \) ovvero $ x - 2 = 0 $.

Queste due rette si intersecano nel punto P(2;3).

Sostituisco le due equazioni $ y-3=0 $ e $ x-2=0 $ nell'equazione del fascio di rette.

$$ (ax+by+c) + k \cdot (a'x+b'y+c') = 0 $$

$$ (y-3) + k \cdot (x-2) = 0 $$

$$ y = - k \cdot (x-2) +3 $$

$$ y = - kx + 2k +3 $$

Dove k è la pendenza che varia, generando infinite rette che passano tutte per il punto P(2,3).

Ogni valore di k determina una diversa retta nel fascio.

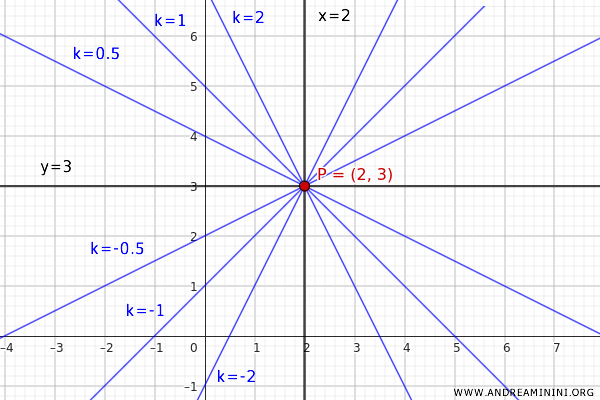
E così via.