Il teorema della perpendicolare di una retta a un punto
Dato un punto P e una retta r, esiste una e una sola perpendicolare alla retta r che passa per il punto P.
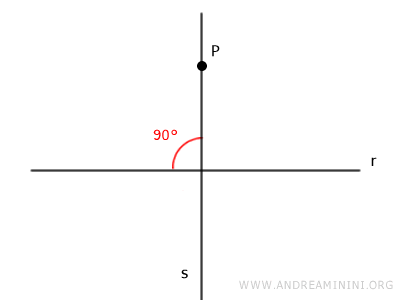
In pratica, se considero un punto P qualsiasi del piano e una retta r che non necessariamente passa per il punto P, esiste una sola retta s perpendicolare a r che passa per il punto P.
Il punto in cui la retta perpendicolare interseca la retta r è detto piede della perpendicolare.
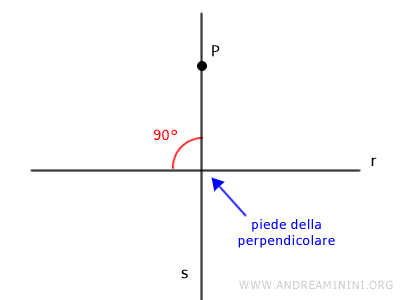
Questo teorema è conosciuto anche come teorema di esistenza e unicità della perpendicolare di una retta in un punto.
La dimostrazione
Considero un punto $ P $ esterno alla retta $ r $ e la perpendicolare $ s \perp r $ che passa per il punto.
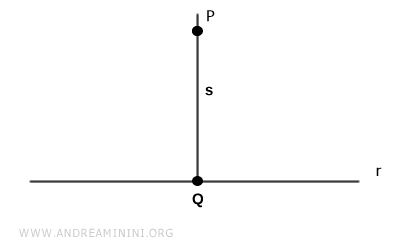
Il punto $ Q $ è il piede della perpendicolare $ s $.
Prendo due punti $ A $ e $ B $ non coincidenti che si trovano sulla retta $ r $ e sono equidistanti dal punto $ Q $.
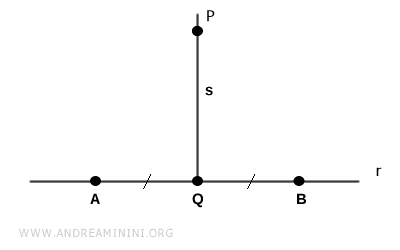
Ora traccio i segmenti $ AP $ e $ BP $.
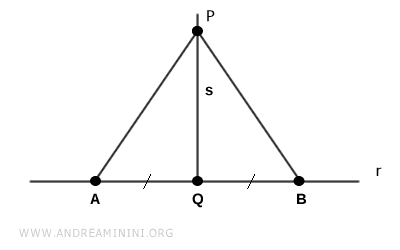
Per costruzione il segmento $ PQ $ è la bisettrice dell'angolo $ A \hat P B $ e $ PQ \in s $ appartiene alla perpendicolare $ s $.
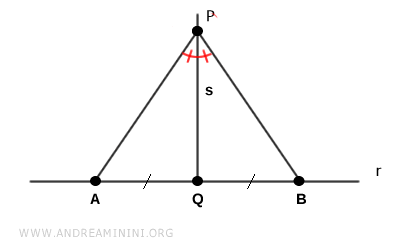
Sapendo che la bisettrice di un angolo è unica, deduco che anche la perpendicolare $ s $ è unica.
La dimostrazione alternativa
La dimostrazione si suddivide in due parti.
Devo infatti distinguere la situazione in cui il punto P appartiene alla retta "r" e quello in cui non vi appartiene.
A] Il punto P appartiene alla retta ( P ∈ r )
Considero una retta r nel piano e un punto P qualsiasi appartenente alla retta r.
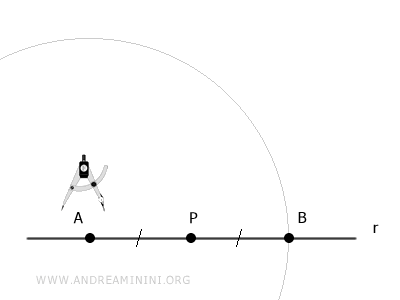
Punto il compasso sul punto P e con un apertura qualsiasi individuo altri due punti A e B sulla retta.
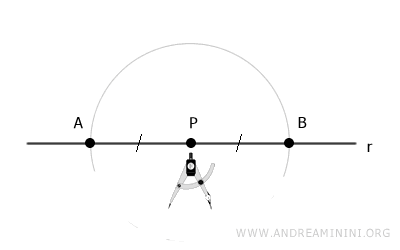
I punti A e B sono equidistanti dal punto P, quindi i segmenti AP e BP sono congruenti ossia hanno la stessa lunghezza.
$$ AP \cong BP $$
Di conseguenza, il punto P è il punto medio del segmento AP.
A questo punto punto il compasso su A e con apertura AB traccio un arco.
Punto il compasso su B e traccio un secondo arco con la stessa apertura.
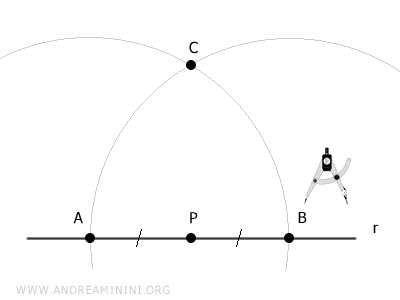
Il punto di intersezione dei due archi è il punto C,
Nota. In realtà, posso utilizzare anche un'apertura diversa da AB, purché sia maggiore di AP per fare in modo che i due archi si intersechino.
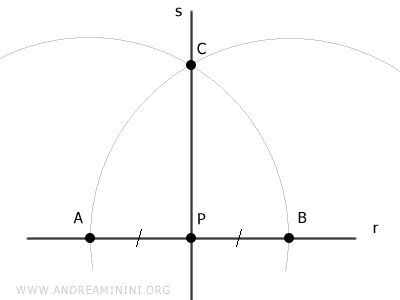
Tra due punti distinti del piano passa una e una sola retta.
Quindi, tra i punti P e C passa una e una sola retta s.
La retta s è perpendicolare alla retta r perché se considero il triangolo ABC, questo è un triangolo isoscele in quanto i lati AC e BC sono congruenti per costruzione (AC≅BC)
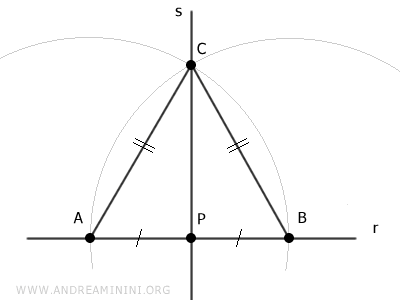
Il segmento CP coincide con la mediana del triangolo perché collega il vertice C con il punto medio P del lato opposto AB.
Sapendo che in un triangolo isoscele la mediana coincide con l'altezza del triangolo, deduco che il segmento CP forma un angolo di 90° rispetto alla base AB.
Pertanto, la retta s che comprende il segmento CP è perpendicolare alla retta r.
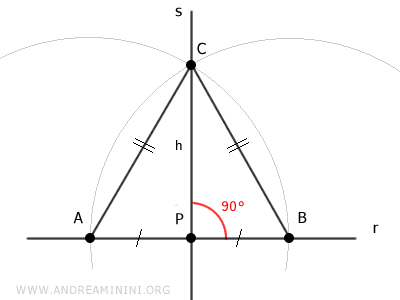
Ho appena dimostrato l'esistenza e l'unicità della retta perpendicolare.
Nota. L'unicità è dimostrata dal fatto che in due punti distinti C e P passa una e una sola retta. Un'ulteriore prova deriva dal fatto che il triangolo ABC è isoscele e nei triangoli isosceli la mediana CP coincide anche con la bisettrice dell'angolo associato al vertice C. Sapendo che esiste una sola bisettrice in un angolo, questa è un'ulteriore prova dell'unicità della retta s.
B] Il punto P non appartiene alla retta ( P ∉ r )
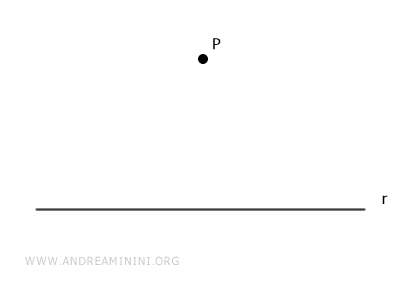
Considero una retta r e un punto P del piano che non appartiene alla retta.
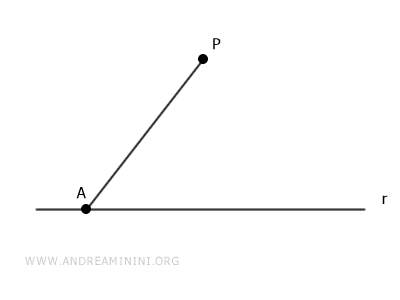
Scelgo a caso un punto A qualsiasi della retta r e traccio un segmento AP.
Centro il compasso sul punto A e con apertura AP traccio un arco.
Il punto di intersezione dell'arco sulla retta r è il punto B.
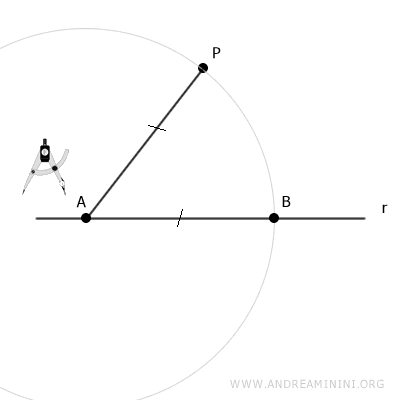
Per costruzione i segmenti AP e AB sono congruenti
$$ \overline{AP} \cong \overline{AB} $$
Punto il compasso sul punto B e con apertura BP traccio un secondo arco.
I due archi si intersecano nel punto P e nel punto C.
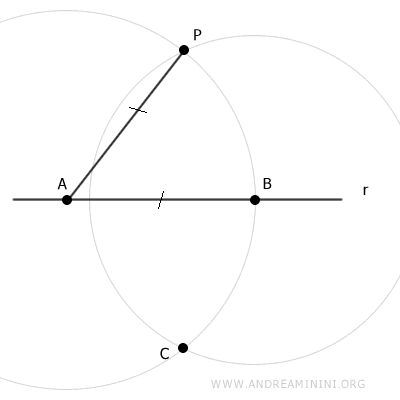
Traccio un segmento CP tra i punti P e C.
Il segmento CP interseca la retta nel punto D.
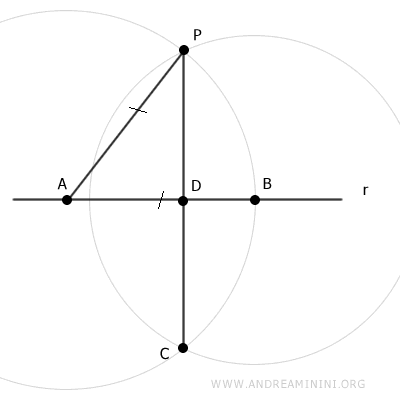 i tre i tre
i tre i tre
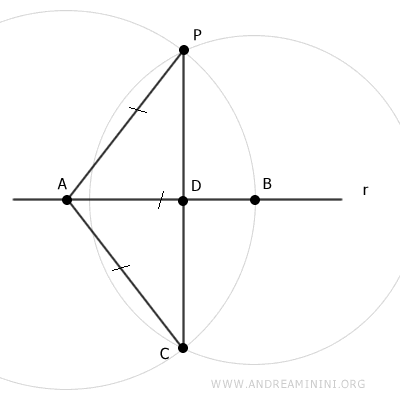
Traccio il segmento AC che per costruzione è congruente con il segmento AP (AC≅AP).
Traccio i segmenti BP e BC che sono congruenti per costruzione (BP≅BC).
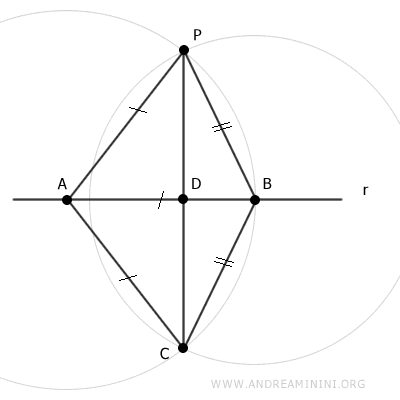
In base al terzo criterio di congruenza dei triangoli (LLL), i due triangoli APB e ACB sono congruenti perché hanno un lato coincidente AB e due lati congruenti AP≅AC e BP≅BC.
$$ APB \cong ACB $$
Quindi, i triangoli APB e ACB hanno gli angoli congruenti nello stesso ordine.
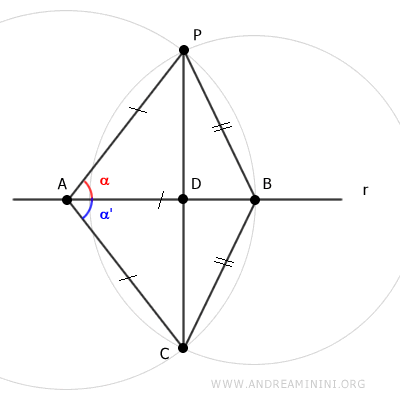
In particolar modo mi interessa sapere che sono congruenti gii angoli α≅α'
Questo mi permette di affermare che anche i triangoli APD e ACD sono congruenti perché hanno un angolo congruente (α≅α'), un lato congruente (AP≅AC) e un lato coincidente (AD).
$$ APD \cong ACD $$
Di conseguenza anche i lati PD e CD sono congruenti (PD≅CD).
Quindi, il punto D è il punto medio del segmento PC.
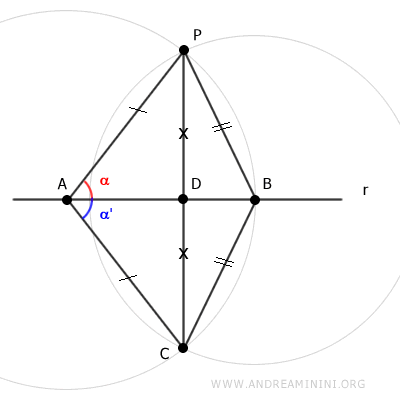
Ora considero il triangolo APC che è un triagolo isoscele perché ha due lati congruenti AP e AC
Il segmento AD è la mediana del triangolo APC perché collega il vertice A con il punto medio D del lato opposto PC.
Nei triangoli isoscele la mediana coincide con l'altezza e la bisettrice.
Nota. Per definizione l'altezza di un triangolo è un segmento che collega un vertice con un punto del lato opposto (o del suo prolungamento) formando un angolo di 90°.
Quindi, il segmento AD è perpendicolare al segmento PC.
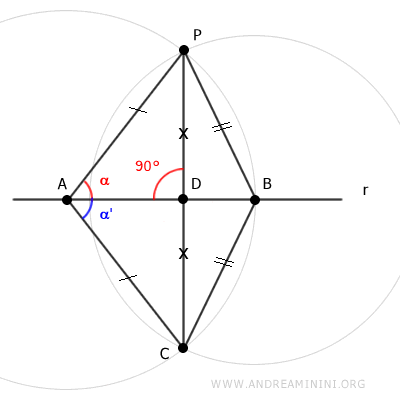
Pertanto, sapendo che tra due punti distinti passa una e una sola retta, la retta s che passa per i punti P e C è perpendicolare alla retta r che passa per i punti A e B.
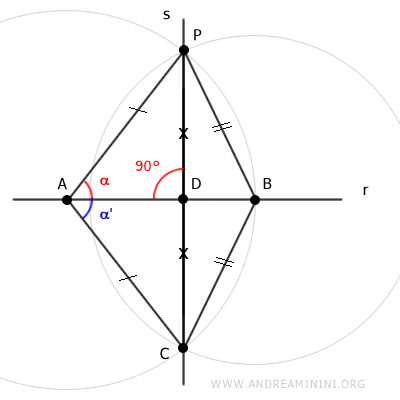
Nota. Oltre al fatto che tra due punti distinti passa una sola retta, l'unicità è dimostrata anche dal fatto che il triangolo APC è isoscele e nei triangoli isosceli la mediana AD coincide con la bisettrice dell'angolo associato al vertice A. Quindi, la retta r è perpendicolare alla retta s e viceversa.
Ho così dimostrato che esiste una e una sola retta s perpendicolare alla retta r passante per il punto C.
$$ r \perp s $$
Verifica. Se prendo un qualsiasi altro punto E della retta r diverso dal punto D, sapendo che il segmento PD è perpendicolare alla retta r, l'unione dei punti PDE forma un triangolo rettangolo.
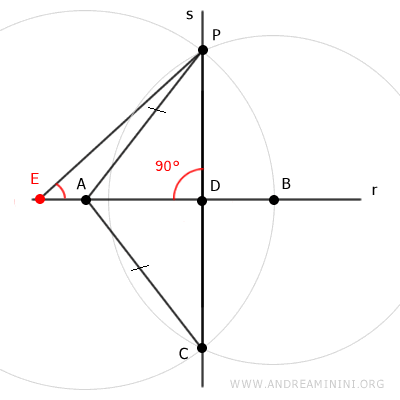
In un triangolo rettangolo solo un angolo può essere un angolo retto (90°). In questo caso è l'angolo retto (90°) che corrisponde al vertice D. Pertanto, gli altri due angoli del triangolo rettangolo PDE devono essere acuti (<90°). Da questo deduco che il segmento PE non può essere perpendicolare alla retta r. Lo stesso discorso vale per qualsiasi punto E della retta r diverso dal punto D.
E così via.
