Il teorema del raggio della circonferenza circoscritta ai poligoni regolari simili
Quando due poligoni regolari con lo stesso numero di lati sono simili, hanno tutti i lati proporzionali e anche il raggio della circonferenza circoscritta e l'apotema hanno lo stesso rapporto di proporzionalità dei lati.
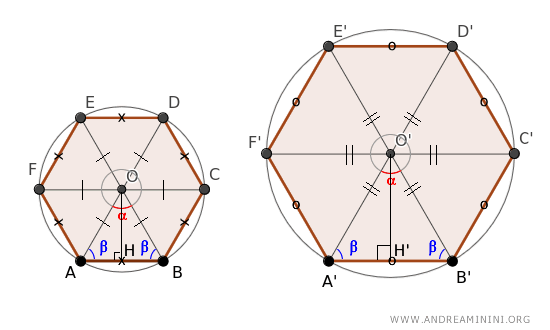
Questo teorema stabilisce che, in presenza di due poligoni regolari simili che condividono lo stesso numero di lati, si verifica una proporzione costante non solo tra i loro lati ma anche tra i raggi delle rispettive circonferenze circoscritte e i loro apotemi.
Ciò significa che il rapporto di proporzionalità che intercorre tra i lati dei due poligoni si riflette ugualmente sul rapporto tra i raggi delle circonferenze circoscritte a ciascun poligono e tra i loro apotemi.
Corollario. Poiché due poligoni regolari con lo stesso numero di lati hanno anche i perimetri nella stessa proporzione (teorema del perimetro dei poligoni regolari), deduco che i raggi delle circonferenze circoscritte e gli apotemi stanno fra loro come i lati omologhi e i perimetri dei due poligoni simili.
Un esempio
Prendo come esempio due esagoni regolari simili.
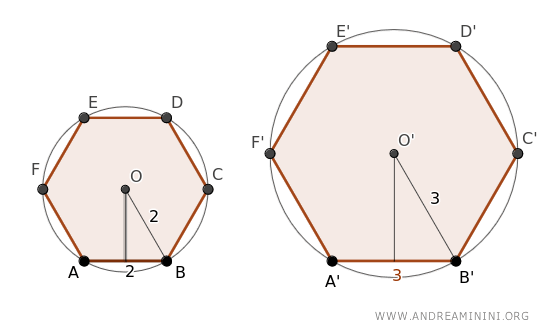
Il primo esagono ha ogni lato di lunghezza 2 mentre il secondo ha ogni lato di lunghezza 3.
$$ AB = BC = CD = DE = EF = AD = 2 $$
$$ A'B' = B'C' = C'D' = D'E' = E'F' = A'D' = 3 $$
Essendo due poligoni regolari, sono entrambi circoscrivibili e la circonferenza ha il raggio rispettivamente uguale a 2 e a 3.
$$ OB = 2 $$
$$ O'B' = 3 $$
E' già evidente che i raggi stanno fra loro come i lati omologhi
$$ OB : O'B' = AB : A'B' $$
$$ 2 : 3 = 2 : 3 $$
$$ 0.6666 = 0.6666 $$
In questo caso, il rapporto di proporzionalità è 0.6666 periodico.
Per trovare gli apotemi calcolo il cateto dei triangoli rettangoli OBH e O'B'H' usando il teorema di Pitagora.
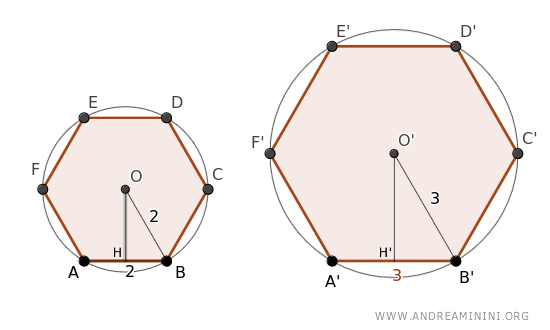
I lati dei triangoli rettangoli sono OB=2 e HB=1 e O'B'=3 e H'B'=1.5
$$ OH = \sqrt{2^2 - 1^2} = \sqrt{3} $$
$$ O'H' = \sqrt{3^2 - 1.5^2} = \sqrt{6.75} $$
I due cateti OH e O'H' coincidono con gli apotemi dei due esagoni.
Infine, calcolo il rapporto tra i due cateti.
$$ \frac{ \sqrt{3} }{ \sqrt{6.75} } = 0.6666 $$
Il rapporto di proporzionalità tra gli apotemi è lo stesso dei raggi delle circonferenze e dei lati omologhi dei poligoni.
La dimostrazione
Considero due poligoni regolari con lo stesso numero di lati.
Ad esempio, due esagoni regolari di diversa grandezza.
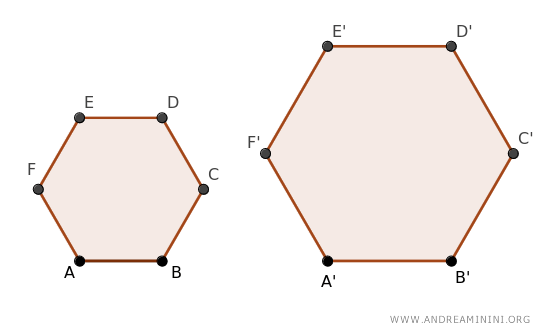
Sono poligoni regolari con lo stesso numero di lati, quindi sono poligoni simili secondo il teorema di similitudine dei poligoni regolari.
Essendo poligoni simili hanno tutti i lati proporzionali con la stessa proporzione.
$$ AB:A'B' = BC:B'C' = CD:C'D' = DE:D'E' = EF:E'F' = AF:A'F' $$
Inoltre, essendo dei poligoni regolari, sono sempre poligoni circoscrivibili da una circonferenza.
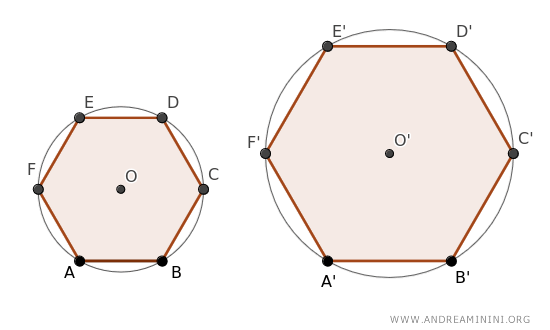
Traccio i segmenti tra il centro O e ogni vertice degli esagoni.
Questi segmenti sono congruenti tra loro in ogni poligono perché coincidono con il raggio della rispettiva circonferenza.
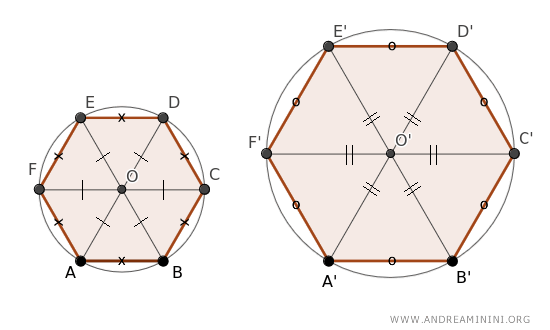
In questo modo ho suddiviso la superficie degli esagoni in sei triangoli.
Questi triangoli sono tutti triangoli isosceli perché i lati obliqui sono congruenti al raggio della rispettiva circonferenza.
Inoltre, per il terzo criterio di congruenza dei triangoli in ciascun poligono i triangoli sono congruenti fra loro perché hanno tutti i lati congruenti nello stesso ordine.
$$ ABO \cong BCO \cong CDO \cong EDO \cong EFO \cong AFO $$
$$ A'B'O' \cong B'C'O' \cong C'D'O' \cong E'D'O' \cong E'F'O' \cong A'F'O' $$
Inoltre, in entrambi i poligoni l'angolo giro al centro della circonferenza viene suddiviso in 6 parti congruenti.
$$ \alpha = \frac{360°}{6} = 60° $$
Quindi tutti i triangoli di entrambi i poligoni hanno l'angolo al vertice O congruente (α=60°).
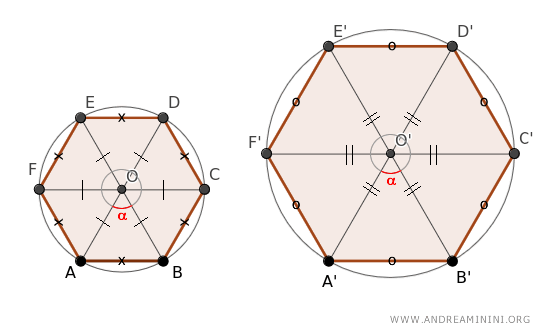
Per il secondo criterio di similitudine tra i triangoli, i triangoli del primo poligono sono simili quelli del secondo poligono, perché hanno un angolo congruente e i lati adiacenti proporzionali.
Essendo triangoli congruenti in ciascun poligono, per semplicità considero solo i triangoli ABO e A'B'O'.
$$ ABO \approx A'B'O' $$
Di conseguenza, i due triangoli hanno tutti i lati proporzionali.
$$ AB:A'B' = OB:O'B' = OA:O'A' $$
Dove AB e A'B' sono i lati dei poligoni mentre OA e O'A' sono i raggi della circonferenza.
Questo dimostra che i raggi delle circonferenze circoscritte stanno ai lati dei poligono regolari nella stessa proporzione.
Nota. I triangoli ABO e A'B'O' sono triangoli isosceli simili. Quindi hanno tutti i lati in proporzione. Pertanto, sono proporzionali anche le altezze rispetto alle basi AB e A'B' ovvero gli apotemi dei poligoni. $$ OH:O'H' = OA:O'A' = AB:A'B' $$

Per verificarlo basta considerare che i triangoli isosceli hanno gli angoli alla base congruenti. Poiché l'angolo al vertice è congruente (α) i triangoli ABO e A'B'O' hanno anche gli angoli alla base congruenti $$ \beta = \frac{ 180° - \alpha }{2} $$ Pertanto, se dividero i due triangoli isosceli in due triangoli rettangoli AOH e A'O'H, anche questi sono triangoli simili perché, per il secondo criterio di similitudine dei triangoli, hanno due lati proporzionale OA:O'A'=AH:A'H' e l'angolo β tra di essi congruente. Pertanto anche l'altezza è proporzionale. $$ OH:O'H' = OA:O'A' $$ Questo dimostra che l'apotema del poligono ha lo stesso rapporto proporzionale del raggio della circonferenza e del lato del poligono.
E così via.
