Criteri di similitudine dei poligoni con lo stesso numero di lati

Questo teorema è conosciuto come il teorema di similitudine dei poligoni e mi permette di ridurre il numero di verifiche per stabilire la similitudine tra due poligoni con lo stesso numero n di angoli e lati.

Detto in altre parole

1. Il primo criterio esclude 3 angoli consecutivi
2. Il secondo criterio esclude 2 angoli consecutivi e i lati tra di essi
3. Il terzo confronto esclude 1 angolo e i due lati adiacenti ad esso

Nota. In generale per determinare la similitudine tra due poligoni dovrei verificare la congruenza tra tutti gli angoli corrispondenti e la stessa proporzionalità su tutti i lati corrispondenti, effettuando un numero maggiore di verifiche.

La spiegazione

La similitudine tra poligoni implica che hanno la stessa forma, ma non necessariamente la stessa dimensione.

Pertanto, per verificare se due poligoni con n angoli e lati sono simili dovrei verificare se sono soddisfatte entrambe le condizioni della similitudine:

• hanno tutti gli angoli corrispondenti congruenti (ovvero hanno la stessa misura)
• hanno i lati corrispondenti sono proporzionali (cioè, il rapporto tra i lati corrispondenti nei due poligoni è costante).

Nota. La sola presenza degli angoli corrispondenti congruenti non è sufficiente a stabilire la similitudine tra due poligoni con più di 3 lati. Ad esempio, un quadrato e un rettangolo hanno gli angoli corrispondenti congruenti (90°) ma non sono figure simili perché i lati non sono proporzionali, ovvero il rapporto tra i lati corrispondenti non è costante.

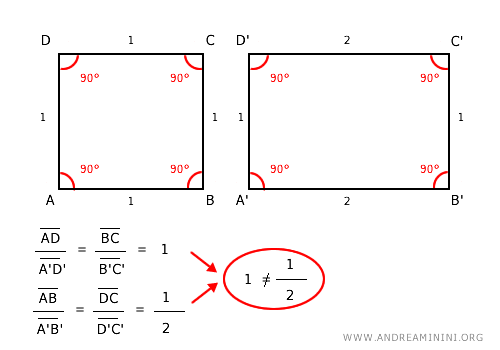
Tuttavia, esistono dei criteri di similitudine che permettono di verificare la similitudine osservando un minore numero di informazioni.

In particolar modo, secondo il teorema di similitudine dei poligoni, ognuna di queste situazioni è una condizione sufficiente di similitudine:

• Due poligoni con n lati sono simili se hanno n-3 angoli consecutivi congruenti e tutti i lati corrispondenti in proporzione. 

  Nota. Questo criterio esclude dalla verifica tre angoli consecutivi. Ad esempio, questi due pentagoni hanno n=5 angoli. Quindi, posso verificare la congruenza solo su n-3 angoli consecutivi, ovvero su 2 angoli consecutivi. In questo esempio ho scelto di verificare gli angoli α= α' e β=β'. Oltre a questo devo verificare che tutti i lati corrispondenti abbiano lo stesso rapporto di proporzionalità.
  

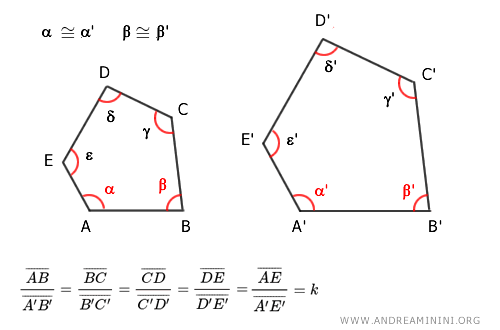
• Due poligoni con n lati sono simili se hanno n-2 angoli consecutivi congruenti e i rispettivi lati adiacenti in proporzione.

  Nota. Questo criterio esclude dalla verifica due angoli consecutivi ed esclude il lato tra di essi. Ad esempio, due pentagoni hanno n=5 angoli. Quindi, posso verificare la congruenza solo su n-2 angoli consecutivi, ovvero su 3 angoli consecutivi. In questo esempio scelgo di verificare la congruenza sugli angoli α= α' , β=β' e γ=γ' e la proporzionalità sui lati adiacenti ad essi. Ho escluso dall'analisi i due angoli restanti δ e ε e il lato DE tra di essi.
  

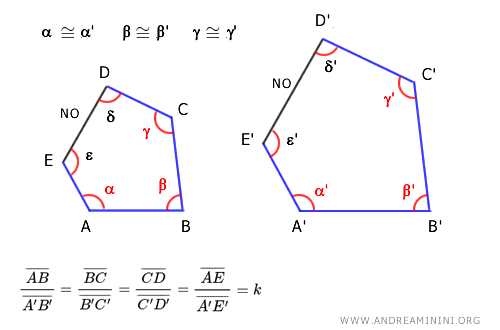
• Due poligoni con n lati sono simili se hanno n-1 angoli corrispondenti congruenti e tutti i lati non adiacenti all'angolo escluso in proporzione

  Nota. Questo criterio esclude dalla verifica un angolo e i due lati adiacenti all'angolo escluso. Ad esempio, in un pentagono con n=5 lati posso verificare la congruenza solo su n-1 angoli, ovvero su 4 angoli, e il rapporto di proporzionalità solo sui lati tra di essi. Se escludo l'angolo ε, mi basta verificare la congruenza sugli angoli corrispondenti restanti α≅α' , β≅β' , γ≅γ' e  δ≅δ' e la proporzionalità su tutti i lati, tranne sui lati AE e DE adiacenti all'angolo escluso ε.
  

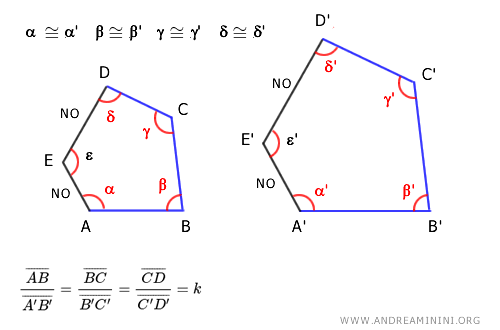
La similitudine nei poligoni regolari

Nel caso dei poligoni regolari posso usare un ulteriore criterio di similitudine.

Due poligoni regolari sono simili se hanno lo stesso numero n di lati.

Si tratta di un corollario del teorema di similitudine dei poligoni.

La dimostrazione

Per ipotesi iniziale considero due poligoni regolari con n lati.

Ad esempio, due pentagoni regolari con n=5 lati ma il discorso vale per qualsiasi numero di lati.

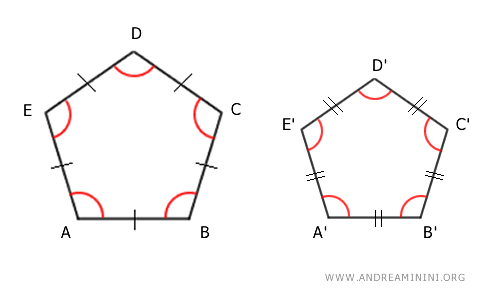
Un poligono è detto "poligono regolare" se ha tutti gli angoli e i lati congruenti, ovvero della stessa lunghezza.

1] Tutti gli angoli congruenti

In un poligono regolare gli angoli sono per definizione tutti congruenti e l'ampiezza di ciascun angolo è determinata dal numero n dei lati del poligono regolare:

$$ \frac{n-2}{n} \cdot 180° $$

Questo significa che tutti gli angoli di un poligono regolare sono congruenti tra loro.

Ad esempio, nel caso di un pentagono regolare con n=5 lati hanno tutti un'ampiezza di 108°.

$$ \frac{n-2}{n} \cdot 180° = \frac{5-2}{5} \cdot 180° = \frac{3}{5} \cdot 180° = 108° $$

Pertanto se due poligoni regolari ABCDE e A'B'C'D'E' hanno lo stesso numero di lati, ad esempio n=5, deduco che abbiano anche le coppie di angoli corrispondenti congruenti ovvero con la stessa ampiezza.

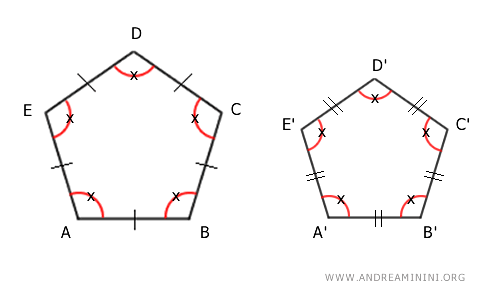
2 Tutti i lati congruenti

In un poligono regolare tutti i lati sono congruenti, ovvero hanno la stessa lunghezza.

Quindi tutti i lati del primo poligono ABCDE sono congruenti tra loro:

$$ \overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DE} \cong \overline{AD} $$

Per la stessa ragione sono congruenti anche tutti i lati del secondo poligono A'B'C'D'E':

$$ \overline{A'B'} \cong \overline{B'C'} \cong \overline{C'D'} \cong \overline{D'E'} \cong \overline{A'D'} $$

Prendo una coppia di lati corrispondenti dei due poligoni, ad esempio AB e A'B', e calcolo il loro rapporto di proporzione.

$$ \frac{ \overline{AB}}{ \overline{A'B'} } = k $$

Sapendo che tutti i lati del primo poligono sono tra loro congruenti, e lo stesso accade anche nel secondo poligono, deduco che anche gli altri lati corrispondenti hanno lo stesso rapporto di proporzionalità k.

Ad esempio, sapendo AB≅BC e A'B'≅B'C sono congruenti, allora anche il rapporto tra i lati BC e B'C' è uguale a k.

$$  \frac{ \overline{AB}}{ \overline{A'B'} } = \frac{ \overline{BC}}{ \overline{B'C'} } = k $$

Lo stesso ragionamento posso ripeterlo per tutti gli altri lati restanti.

$$ \frac{ \overline{CD}}{ \overline{C'D'} } = k $$

$$ \frac{ \overline{DE}}{ \overline{D'E'} } = k $$

$$ \frac{ \overline{AE}}{ \overline{A'E'} } = k $$

Quindi, se due poligoni regolari hanno due lati corrispondenti proporzionali, deduco che siano proporzionali nella stessa misura anche gli altri lati corrispondenti dei due poligoni.

Conclusione

In conclusione, in due poigoni regolari con lo stesso numero di lati entrambe le condizioni della similitudine sono soddisfatte:

1. tutti gli angoli corrispondenti sono congruenti
2. tutti i lati sono proporzionali nello stesso ordine

Pertanto i due poligoni sono simili.

Nota. In altre parole, nel caso di due poligoni regolari con lo stesso numero di lati, non è necessario verificare la congruenza degli angoli o la proporzionalità dei lati individualmente. Per definizione, in poligoni regolari tutti gli angoli sono uguali tra loro e tutti i lati hanno la stessa lunghezza, il che implica che se due di questi poligoni hanno lo stesso numero di lati, la congruenza degli angoli e la proporzionalità dei lati sono automaticamente garantite, confermando la loro similitudine.

E così via.