La similitudine

La similitudine è un tipo di affinità che conserva la congruenza fra gli angoli e un rapporto di proporzionalità k costante tra i lati corrispondenti. E' una trasformazione geometrica che si ottiene tramite la composizione di una omotetia e una isometria.

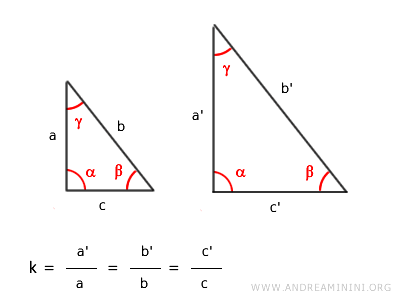
Si tratta di una trasformazione geometrica che mantiene la forma ma non le dimensioni.

In altre parole, due figure sono dette figure simili se si corrispondono in una similitudine, ovvero se hanno:

1. I lati corrispondenti paralleli (affinità)
2. Gli angoli corrispondenti congruenti, ovvero di uguale ampiezza.
3. I lati corrispondenti proporzionali e il rapporto di proporzionalità (k) è lo stesso per tutti i lati corrispondenti.

Questo equivale a dire che una figura simile a un'altra mantiene la stessa forma ma modifica le sue dimensioni.

 

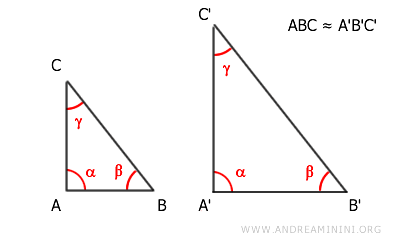
Il simbolo della similitudine sono due onde sovrapposte "≈".

Ad esempio, per indicare che le figura ABC e A'B'C' sono simili scrivo:

$$ ABC ≈ A'B'C' $$

I lati e gli angoli che si corrispondono in una similitudine sono detti lati omologhi e angoli omologhi.

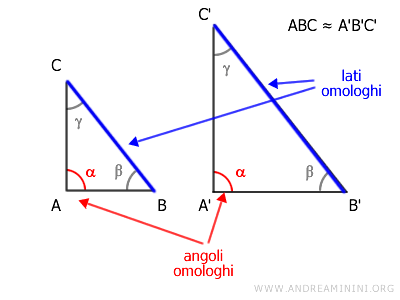
Nota. Nei due triangoli simili, i lati omologhi sono quelli che si trovano in posizione opposta rispetto agli angoli congruenti dei due triangoli. In altre parole, i lati omologhi sono i lati opposti agli angoli congruenti.

Il rapporto di proporzionalità (k) è lo stesso per tutti i lati omologhi ed è detto anche rapporto di similitudine o rapporto di scala.

Pertanto, gli invarianti di una similitudine sono le ampiezze degli angoli e i rapporti fra i segmenti corrispondenti omologhi.

Un esempio pratico di similitudine è la riproduzione di una fotografia in un formato più grande rispetto all'originale. Ad esempio, ingrandire una foto per metterla in una cornice. La foto originale e quella ingrandita hanno la stessa forma ma dimensioni diverse.

In modo analogo la similitudine si estende anche nello spazio a tre dimensioni tra i solidi che hanno gli angoli corrispondenti congruenti e hanno i segmenti corrispondenti paralleli (affinità spaziale) con lo stesso rapporto di proporzionalità |k|.

Il rapporto di similitudine

Quando due figure sono simili, le loro corrispondenti lunghezze dei lati sono in proporzione, e questa proporzione è chiamata il fattore di scala della similitudine.

• Ingrandimento (k>1)
  Se il rapporto di similitudine è maggiore di 1 la figura risulta ingrandita in scala 1:k.

  
  Ad esempio, se k=2 la figura è ingrandita in una scala 1:2. Se il fattore di scala è 2, tutte le lunghezze nella figura simile sono il doppio di quelle nella figura originale.

• Isometria (k=1)
  Se il rapporto di similitudine è uguale a 1 la trasformazione geometrica rientra nelle isometrie (es. rotazioni, traslazioni, riflessioni, ecc.)
  
• Riduzione (0<k<1)
  Se il rapporto di similitudine è compreso tra 0 e 1, la figura risulta ridotta in scala 1:k.
  

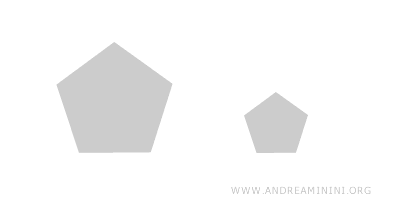
  Ad esempio, se k=0.5 la figura è ridotta in scala 1:0.5 ovvero, in modo del tutto equivalente, in scala 2:1

In tutti i casi le figure simili mantengono la stessa forma.

Poligoni simili

Due poligoni sono simili se hanno i lati corrispondenti in proporzione costante e gli angoli corrispondenti della stessa ampiezza (angoli corrispondenti congruenti).

In generale, tutti i poligoni regolari e i cerchi sono simili tra loro.

I criteri di similitudine del triangolo

Ci sono alcuni criteri principali che stabiliscono la similitudine tra due figure geometriche. In particolare tra i triangoli.

• Criterio AAA (Angolo-Angolo-Angolo)
  Due triangoli sono simili se hanno corrispondenti angoli congruenti.
  

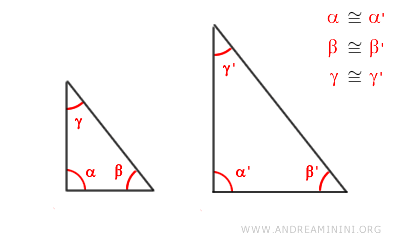
  Nota. In realtà, per determinare la similitudine tra due triangoli basta che ci siano due angoli corrispondenti congruenti. Se due triangoli hanno due angoli congruenti, allora anche il terzo angolo sarà congruente a causa della proprietà che la somma degli angoli interni in un triangolo è sempre uguale a 180 gradi.

• Criterio LAL (Lato-Angolo-Lato)
  Due triangoli sono simili se due lati di un triangolo sono proporzionali ai due corrispondenti lati dell'altro triangolo, e l'angolo compreso tra i due lati è uguale in entrambi i triangoli.
  
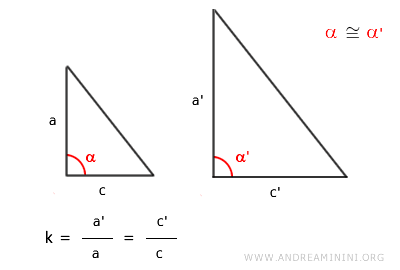
• Criterio LLL (Lato-Lato-Lato)
  Due triangoli sono simili se i lati di uno sono proporzionali ai corrispondenti lati dell'altro triangolo. Questo significa che tutte le lunghezze dei lati di un triangolo sono in uno stesso rapporto costante con le lunghezze dei lati corrispondenti dell'altro triangolo.
  

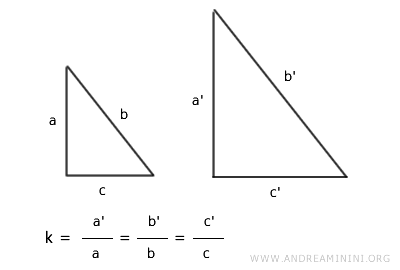
Le equazioni della similitudine

La similitudine posso rappresentarla nel piano cartesiano Oxy tramite questo sistema di equazioni in forma matriciale.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = M \cdot \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} c \\ d \end{pmatrix} $$

Dove la matrice M cambia a seconda se si tratta di una similitudine diretta o invertente

• Similitudine diretta $$ M =  \begin{pmatrix} a & -b \\ b &a \end{pmatrix} $$
• Similitudine invertente $$ M =  \begin{pmatrix} a & b \\ b & -a \end{pmatrix} $$

Quindi, nel caso di una similitudine diretta il sistema di equazioni cartesiane è il seguente:

$$ \begin{cases} x' = ax-by  + c  \\ \\ y' = bx+ay +d \end{cases} $$

Nella similitudine inversa, invece, il sistema di equazioni cartesiane è il seguente:

$$ \begin{cases} x' = ax+by  + c  \\ \\ y' = bx-ay +d \end{cases} $$

In entrambi i casi il rapporto di similitudine k è il seguente:

$$ k = \sqrt{a^2+b^2} $$

In alternativa, posso rappresentare la similitudine anche in questa forma trigonometrica: $$ \begin{cases} x' = k \cdot ( x \cos \alpha \pm y \sin \alpha ) \\ \\ y' = k \cdot ( x \sin \alpha \pm y \cos \alpha ) \end{cases} $$

Osservazioni

Alcune osservazioni e note a margine sulla similitudine

• La similitudine è equivalente alla composizione di una omotetia e una isometria
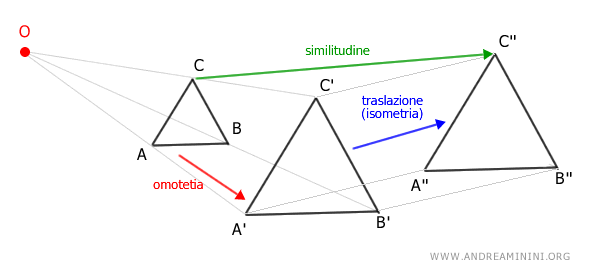
  Nel piano la similitudine equivale a una composizione geometrica di una omotetia e una isometria (traslazione, rotazione, simmetria centrale o assiale, identità), o viceversa. Ecco un esempio pratico di prodotto di un'omotetia e di una isometria.
  
  
• Due figure congruenti sono anche figure simili
  Due figure geometriche congruenti sono anche figure simili, perché la congruenza posso vederla come la composizione di una omotetia con centro qualsiasi e un rapporto di proporzionalità uguale 1 seguita o preceduta da una isometria qualsiasi (identità, traslazione, rotazione, simmetria centrale o assiale).
• Il prodotto tra similitudini
  Il prodotto tra due similitudini con rapporto di scala k₁ e k₂ è uguale alla similitudine con rapporto k₁·k₂.
• Centro della similitudine
  Nel piano una similitudine che non sia una traslazione ha sempre un punto fisso, ovvero un invariante della trasformazione che corrisponde a se stesso detto "centro della similitudine".
• Similitudini dirette e indirette
  Nel piano una similitudine è diretta se conserva lo stesso orientamento rispetto al piano. Viceversa, se non lo mantiene, è una similitudine indiretta.
• Il rapporto tra le aree di due figure simili
  Nel piano due figure simili con un rapporto di similitudine k, hanno il rapporto tra le loro aree pari al quadrato del rapporto di similitudine ovvero k².
• l rapporto tra i volumi di due solidi simili
  Nello spazio a tre dimensioni due solidi simili con un rapporto di similitudine k, hanno il rapporto tra i loro volumi pari al cubo del rapporto di similitudine ovvero k³.

E così via.