Come ottenere l'equazione della circonferenza a partire dal raggio e dal centro
L'equazione della circonferenza in un piano cartesiano può essere ottenuta conoscendo la lunghezza del raggio (r) e le coordinate del centro C(x0,y0) tramite questa formula: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
Questa equazione rappresenta tutti i punti \((x, y)\) che si trovano a una distanza \(r\) dal centro \((x_0, y_0)\).
Esempio pratico
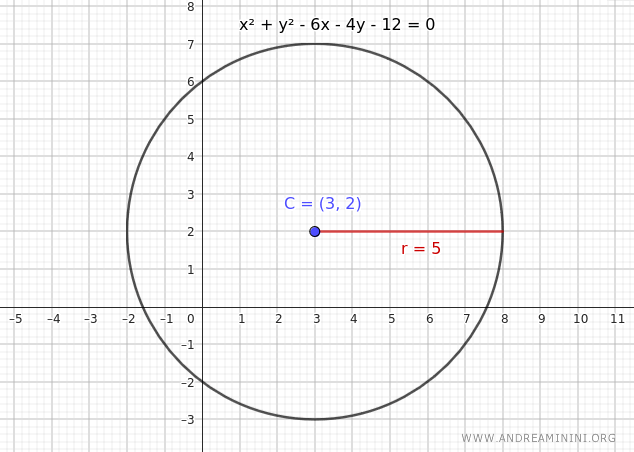
In questo problema conosco il centro della circonferenza \( C(3, 2) \) e il raggio \( r = 5 \).
Per trovare l'equazione della circonferenza applico la formula:
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
In questo caso le coordinate del centro C(3,2) sono x0=3 e y0=2 mentre il raggio è r=5
$$ (x - 3)^2 + (y - 2)^2 = 5^2 $$
$$ (x - 3)^2 + (y - 2)^2 = 25 $$
L'equazione \((x - 3)^2 + (y - 2)^2 = 25\) rappresenta tutti i punti \((x, y)\) che sono a una distanza di 5 unità dal centro della circonferenza \( (3, 2) \).
Per ottenere l'equazione in forma generale basta svolgere tutti i calcoli algebrici, in questo caso i due quadrati dei binomi.
$$ (x - 3)^2 + (y - 2)^2 = 25 $$
$$ x^2 - 6x + 9 + y^2 -4y + 4 - 25 = 0 $$
$$ x^2 + y^2 - 6x -4y - 12 = 0 $$
Questo è un esempio pratico di come si determina l'equazione di una circonferenza noto il centro e il raggio.
Nota. Per verificare se un punto appartiene alla circonferenza, basta sostituire le coordinate del punto nell'equazione e controllare se l'equazione è soddisfatta. Ad esempio, per verificare se il punto P(6,6) è un punto della circonferenza, sostituisco x=6 e y=6 nell'equazione. $$ (x - 3)^2 + (y - 2)^2 = 25 $$ $$ (6 - 3)^2 + (6 - 2)^2 = 25 $$ $$ 3^2 + 4^2 = 25 $$ $$ 9 + 16 = 25 $$ $$ 25=25 $$ Poiché la distanza è uguale al raggio, il punto (6,6) si trova sulla circonferenza, confermando che l'equazione è corretta. In alternativa, posso sostituire x=6 e y=6 nell'equazione generale della circonferenza. Il risultato finale è lo stesso. $$ x^2 + y^2 - 6x -4y - 12 = 0 $$ $$ 6^2 + 6^2 - 6 \cdot 6 -4 \cdot 6 - 12 = 0 $$ $$ 36 + 36 - 36 -24 - 12 = 0 $$ $$ 0 = 0 $$
La dimostrazione
Per ipotesi iniziale conosco il centro della circonferenza: \(C(x_0, y_0)\) e il raggio della circonferenza: \(r\)
Devo dimostrare che l'equazione della circonferenza nel piano cartesiano è \((x - x_0)^2 + (y - y_0)^2 = r^2\).
Per definizione una circonferenza è definita come il luogo dei punti nel piano che sono equidistanti da un punto fisso, chiamato centro. La distanza costante è il raggio \(r\).
Quindi, se prendo un punto \(P(x, y)\) qualsiasi sulla circonferenza, la distanza tra \(P(x, y)\) e il centro \(C(x_0, y_0)\) deve essere uguale al raggio \(r\).
La formula della distanza tra due punti \((x, y)\) e \((x_0, y_0)\) sul piano cartesiano è:
$$ d = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$
In questo caso la distanza (d) deve essere uguale al raggio (r) della circonferenza ossia d=r.
$$ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r $$
Per eliminare la radice quadrata, applico la proprietà invariantiva delle equazioni ed elevo al quadrato entrambi i lati dell'equazione:
$$ \sqrt{(x - x_0)^2 + (y - y_0)^2})^2 = r^2 $$
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
Questa equazione rappresenta tutti i punti \((x, y)\) che sono a una distanza \(r\) dal centro \(C(x_0, y_0)\).
Ho così dimostrato la formula dell'equazione della circonferenza a partire dal centro \(C(x_0, y_0)\) e dal raggio \(r\).
E così via.
